分治之快排和归并-CSDN博客

分治的基本了解

分治之快排

分治的基本了解

分治即分治法，是一种重要的算法设计策略。它的基本思想是将一个规模较大的问题分解为若干个规模较小的子问题，这些子问题相互独立且与原问题类型相同，然后递归的求解这些子问题，最后将子问题的解合并起来得到原问题的解

接下来通过例题来介绍

分治之快排

1.第一题

OJ传送门 LeetCode<75> 颜色分类

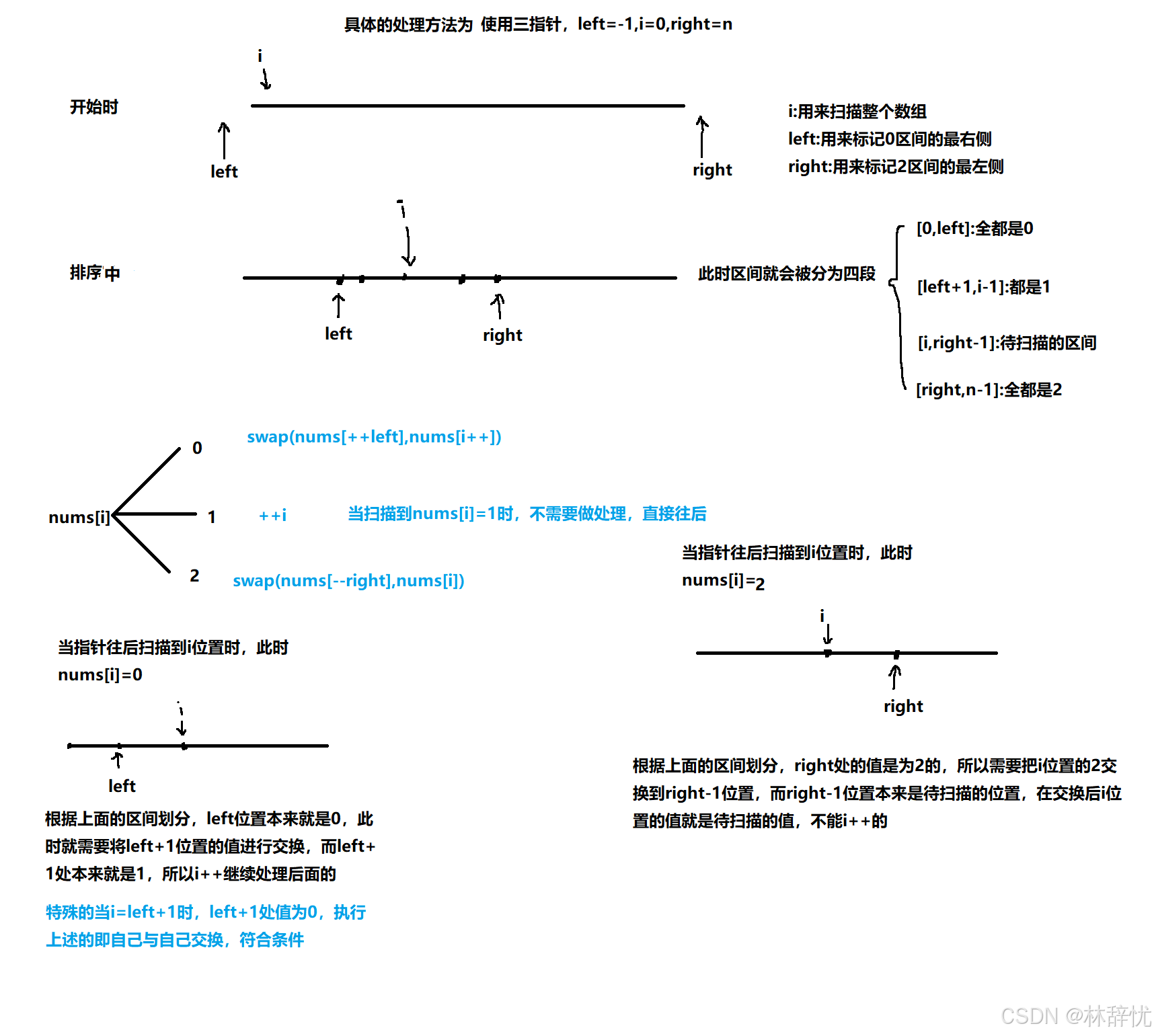
具体代码：

 void sortColors(vector<int>& nums) 
    {
        qsort(nums,0,nums.size());
    }

    void qsort(vector<int>& nums,int l,int r)
    {
        int i=0,left=l-1,right=r;
        while(i<right)//注意循环条件
        {
            if(nums[i]==0) swap(nums[++left],nums[i++]);
            else if(nums[i]==1) ++i;
            else swap(nums[--right],nums[i]);
        }
    }

2.第二题

OJ传送门 LeetCode<912> 排序数组

具体代码：

vector<int> sortArray(vector<int>& nums) 
    {
        qsort(nums,0,nums.size()-1);
        return nums;
    }

   void qsort(vector<int>& nums,int l,int r)
    {
        if(l>=r) return;
        //使用三路划分来解决
        int key=GetRand(nums,l,r);
        int left=l-1,right=r+1,i=l;
        while(i<right)
        {
            if(nums[i]<key) swap(nums[++left],nums[i++]);
            else if(nums[i]==key) ++i;
            else swap(nums[--right],nums[i]);
        }

        //[l,left][left+1,right-1][right,r]
        qsort(nums,l,left);
        qsort(nums,right,r);
    }

    int GetRand(vector<int>& nums,int left,int right)
    {
        return nums[rand()%(right-left+1)+left];
    }

3.第三题

OJ传送门 LeetCode<215> 数组中的第K个最大元素

具体代码：

int findKthLargest(vector<int>& nums, int k) 
    {
        return qsort(nums,0,nums.size()-1,k);
    }

    int qsort(vector<int>& nums,int l,int r,int k)
    {
        if(l>=r) return nums[l];
        //数组分三块
        int key=GetRand(nums,l,r);
        int left=l-1,right=r+1,i=l;
        while(i<right)
        {
            if(nums[i]<key) swap(nums[++left],nums[i++]);
            else if(nums[i]==key) ++i;
            else swap(nums[--right],nums[i]);
        }

        //分情况讨论
        int c=r-right+1,b=right-left-1;
        if(c>=k) return qsort(nums,right,r,k);
        else if(b+c>=k) return key;
        else return qsort(nums,l,left,k-b-c);
    }

    int GetRand(vector<int>& nums,int left,int right)
    {
        return nums[rand()%(right-left+1)+left];
    }

4.第四题

具体代码：

 vector<int> smallestK(vector<int>& nums, int k) 
    {
        qsort(nums,0,nums.size()-1,k);
        return {nums.begin(),nums.begin()+k};
    }

    void qsort(vector<int>& nums,int l,int r,int k)
    {
        if(l>=r) return;
        
        int left=l-1,right=r+1,i=l;
        int key=GetRand(nums,l,r);
        while(i<right)
        {
            if(nums[i]<key) swap(nums[++left],nums[i++]);
            else if(nums[i]==key) ++i;
            else swap(nums[--right],nums[i]);
        }

        //分类讨论
        int a=left-l+1,b=right-left-1;
        if(a>=k) qsort(nums,l,left,k);
        else if(a+b>=k) return;
        else qsort(nums,right,r,k-a-b);
    }

    int GetRand(vector<int>& nums,int left,int right)
    {
        return nums[rand()%(right-left+1)+left];
    }

分治之归并

1.第一题

OJ传送门 LeetCode<912> 排序数组

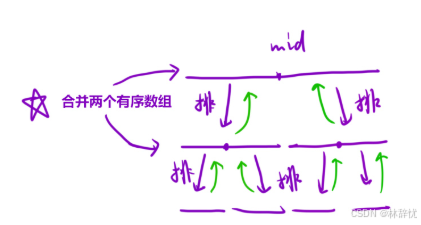
具体代码：

    vector<int>tmp;
    vector<int> sortArray(vector<int>& nums) 
    {
        int n=nums.size();
        tmp.resize(n);
        mergeSort(nums,0,n-1);
        return nums;
    }

    void mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return;

        //1.选择中间点划分区间
        int mid=(left+right)>>1;

        //[left,mid][mid+1,right]
        //2.左右区间进行排序
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);

        //3.合并两个有序数组
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid && cur2<=right)
        tmp[i++]=nums[cur1]<=nums[cur2]?nums[cur1++]:nums[cur2++];
        
        //4.处理未结束的数组
        while(cur1<=mid) tmp[i++]=nums[cur1++];
        while(cur2<=right) tmp[i++]=nums[cur2++];

        //5.还原
        for(int i=left;i<=right;++i)
            nums[i]=tmp[i-left];
    }

2.第二题

OJ传送门 LeetCode<LCR 170> 交易逆序对的总数

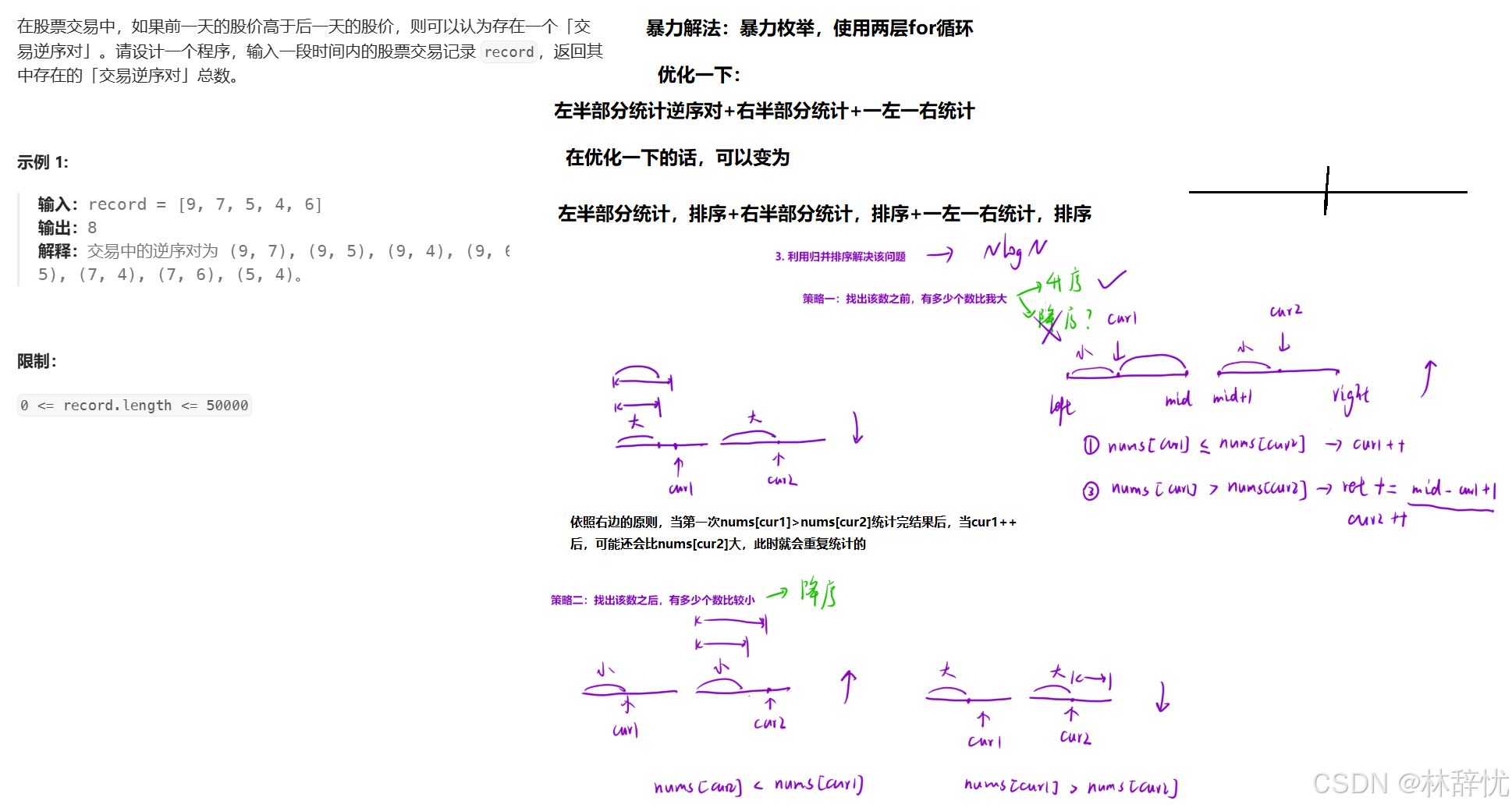
具体代码：

int tmp[50010];
    int reversePairs(vector<int>& record) 
    {
        return mergeSort(record,0,record.size()-1);
    }

    int mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;

        int ret=0;//统计结果
        int mid=(left+right)>>1;
        //[left,mid][mid+1,right]
        ret+=mergeSort(nums,left,mid);
        ret+=mergeSort(nums,mid+1,right);

        //一左一右的计数
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid && cur2<=right)// 升序的时候
        {
            if(nums[cur1]<=nums[cur2])
            tmp[i++]=nums[cur1++];
            else
            {
                ret+=mid-cur1+1;
                tmp[i++]=nums[cur2++];
            }
        }

        //处理排序
        while(cur1<=mid) tmp[i++]=nums[cur1++];
        while(cur2<=right) tmp[i++]=nums[cur2++];

        //还原
        for(int i=left;i<=right;++i)
        nums[i]=tmp[i-left];

        return ret;
    }

3.第三题

OJ传送门LeetCode<315>计算右侧小于当前元素的个数

画图分析：

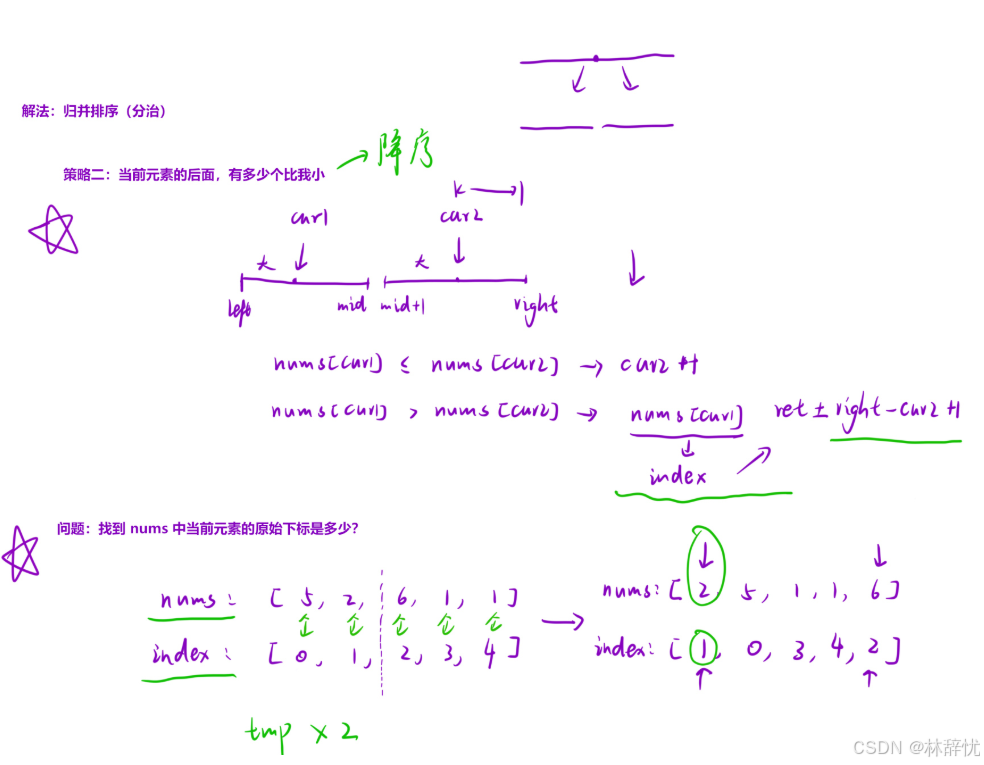
具体代码：

class Solution 
{
    vector<int> ret;
    vector<int> index;//记录nums中当前元素的原始下标
    int tmpNums[500010];
    int tmpIndex[500010];

public:
    vector<int> countSmaller(vector<int>& nums) 
    {
        int n=nums.size();
        ret.resize(n);
        index.resize(n);

        //初始化index数组
        for(int i=0;i<n;++i)
            index[i]=i;
        
        mergeSort(nums,0,n-1);
        return ret;
    }

    void mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return ;

        //1.根据中间元素划分区间
        int mid=(left+right)>>1;
        //[left,mid] [mid+1,right]

        //2.先处理左右两部分
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);

        //3.处理一左一右的情况
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid && cur2<=right)
        {
            if(nums[cur1]<=nums[cur2])
            {
                tmpNums[i]=nums[cur2];
                tmpIndex[i++]=index[cur2++];
            }
            else
            {
                ret[index[cur1]]+=right-cur2+1;
                tmpNums[i]=nums[cur1];
                tmpIndex[i++]=index[cur1++];
            }
        }

        //处理剩下的排序过程
        while(cur1<=mid)
        {
            tmpNums[i]=nums[cur1];
            tmpIndex[i++]=index[cur1++];
        }
        while(cur2<=right)
        {
            tmpNums[i]=nums[cur2];
            tmpIndex[i++]=index[cur2++];
        }
        for(int j=left;j<=right;++j)
        {
            nums[j]=tmpNums[j-left];
            index[j]=tmpIndex[j-left];
        }
        
    }
};

4.第四题

OJ传送门 LeetCode<493>翻转对

画图分析：

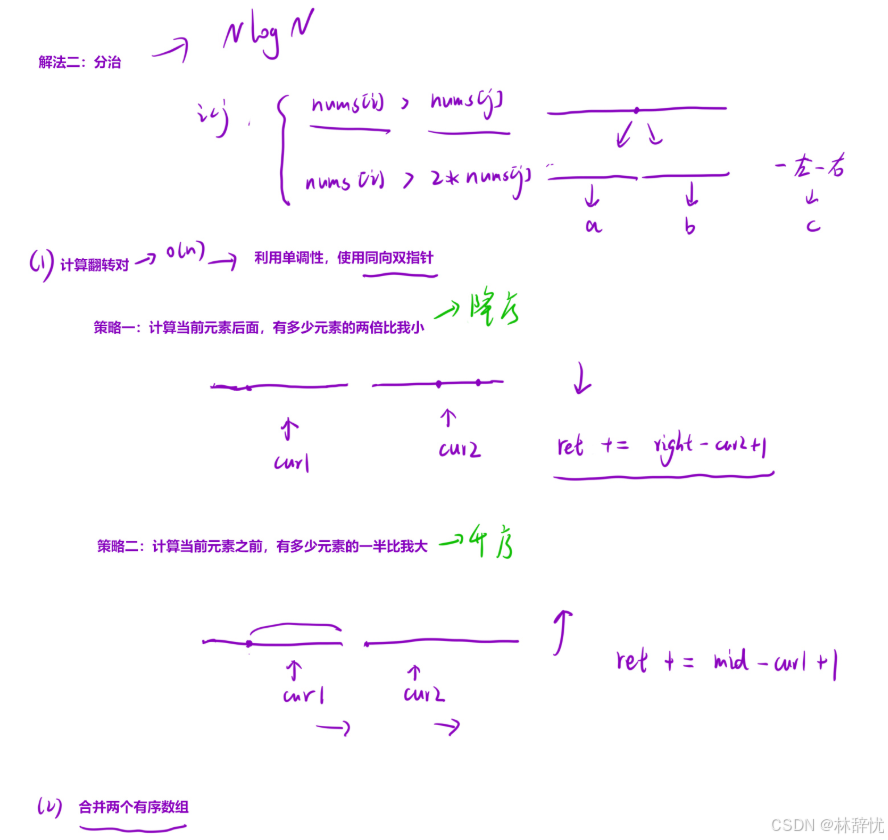具体代码：

class Solution 
{
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) 
    {
        return mergeSort(nums,0,nums.size()-1);
    }

    int mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;
        int ret=0;

        //1.根据中间元素划分区间
        int mid=(left+right)>>1;
        //[left,mid][mid+1,right]

        //2.先计算左右两侧的翻转对
        ret+=mergeSort(nums,left,mid);
        ret+=mergeSort(nums,mid+1,right);

        //3.计算翻转对的数量
        int cur1=left,cur2=mid+1,i=left;
        while(cur1<=mid)//降序的情况
        {
            while(cur2<=right && nums[cur2]>=nums[cur1]/2.0) cur2++;
            if(cur2>right) break;
            ret+=right-cur2+1;
            cur1++;
        }

        //4.合并两个有序数组
        cur1=left,cur2=mid+1;
        while(cur1<=mid && cur2<=right)
            tmp[i++]=nums[cur1]<=nums[cur2]?nums[cur2++]:nums[cur1++];
        while(cur1<=mid) tmp[i++]=nums[cur1++];
        while(cur2<=right) tmp[i++]=nums[cur2++];

        for(int j=left;j<=right;++j)
            nums[j]=tmp[j];
        return ret;
    }
};