本篇博文将总结数学相关的内容,涉及概率组合的一些算法,比较简单。
求1的个数
问题描述
给定一个 32 32 32 位无符号整数 N N N,求整数 N N N 的二进制数中 1 1 1 的个数。
问题分析
方法一
显然:可以通过不断的将整数 N N N 右移,判断当前数字的最低位是否为 1 1 1,直到整数 N N N 为 0 0 0 为止。平均情况下,大约需要 16 16 16 次移位和 16 16 16 次加法。
int OneNumber(int n)
{
int c = 0;
while (n!=0)
{
c += (n & 1);//n末尾最后一位不断和1作与
n >>= 1;//n=n>>1,n右移一位
}
return c;
}
方法二
每次将 n n n 最后一个 1 1 1 清 0 0 0,能清多少次就说明有多少个 1 1 1,只需要 n & = ( n − 1 ) n\verb'&'=(n-1) n&=(n−1) 即可。例如: n = 1010111101 n=1010111101 n=1010111101, n − 1 = 1010111100 n-1=1010111100 n−1=1010111100,两数相与,则必可清除 n n n 最后一位 1 1 1。
int OneNumber2(int n)
{
int c = 0;
while (n!=0)
{
n = n&(n - 1);//将n的最后一个“1”清零
c++;//每清除一个1,c就加一
}
return c;
}
方法三:分治
假定能够求出 N N N 的高 16 16 16 位中 1 1 1 的个数 a a a 和低 16 16 16 位中 1 1 1 的个数 b b b,则 a + b a+b a+b 即为所求。
为了节省空间,用一个 32 32 32 位整数保存 a a a 和 b b b:
- 高 16 16 16 位记录 a a a,低 16 16 16 位记录 b b b;
- ( 0 x F F F F 0000 & N ) (0xFFFF0000\verb'&'N) (0xFFFF0000&N) 筛选得到 a a a;
- ( 0 x 0000 F F F F & N ) (0x0000FFFF\verb'&'N) (0x0000FFFF&N) 筛选得到 b b b;
- ( 0 x F F F F 0000 & N ) + ( 0 x 0000 F F F F & N ) > > 16 (0xFFFF0000\verb'&' N) + (0x0000FFFF\verb'&'N)>>16 (0xFFFF0000&N)+(0x0000FFFF&N)>>16
如何得到高 16 16 16 位和低 16 16 16 位中 1 1 1 的个数 a a a, b b b 呢?
- 分治往往伴随着递归
递归过程:
-
如果二进制数 N N N 是 16 16 16 位,则统计 N N N 的***高 8 8 8 位*** 和***低 8 8 8 位***各自 1 1 1 的数目 a a a 和 b b b,而 a 、 b a、b a、b 用某一个 16 16 16 位数 X X X 存储,则使用 0 x F F 00 、 0 x 00 F F 0xFF00、0x00FF 0xFF00、0x00FF 分别于 X X X 做***与操作***,筛选出 a a a 和 b b b;原问题中的数据是 32 32 32 位,因此分别需要 2 2 2 个 0 x F F 00 / 0 x 00 F F 0xFF00/0x00FF 0xFF00/0x00FF,即 0 x F F 00 F F 00 / 0 x 00 F F 00 F F 0xFF00FF00/0x00FF00FF 0xFF00FF00/0x00FF00FF。
-
如果二进制数是 8 8 8 位,则统计高 4 4 4 位和低 4 4 4 位各自 1 1 1 的数目,使用 0 x F 0 / 0 x 0 F 0xF0/0x0F 0xF0/0x0F 分别做与操作,筛选出高 4 4 4 位和低 4 4 4 位;原问题中的数据是 32 32 32 位,则分别需要 4 4 4 个 0 x F 0 / 0 x 0 F 0xF0/0x0F 0xF0/0x0F,即 0 x F 0 F 0 F 0 F 0 / 0 x 0 F 0 F 0 F 0 F 0xF0F0F0F0/0x0F0F0F0F 0xF0F0F0F0/0x0F0F0F0F。
-
如果是 4 4 4 位则统计高 2 2 2 位和低 2 2 2 位各自 1 1 1 的数目,用 0 x C / 0 x 3 0xC/0x3 0xC/0x3 筛选(高 2 2 2 位 1100 1100 1100 十六进制表示 0 x C 0xC 0xC,低 2 2 2 位 0011 0011 0011 十六进制表示为 0 x 3 0x3 0x3);原问题中的数据是 32 32 32 位,故各需要需要 8 8 8 个 0 x C / 0 x 3 0xC/0x3 0xC/0x3 ,即 0 x C C C C C C C C / 0 x 33333333 0xCCCCCCCC/0x33333333 0xCCCCCCCC/0x33333333。
-
如果是 2 2 2 位则统计高 1 1 1 位和低 1 1 1 位各自 1 1 1 的数目,用 0 x 2 / 0 x 1 0x2/0x1 0x2/0x1 筛选;原问题中的数据是 32 32 32 位,(因为在十六进制中,以四位为一个单位,则高 1 1 1 位为 1010 1010 1010 即为 0 x A 0xA 0xA,需要 8 8 8 个 0 x A 0xA 0xA,同理低 1 1 1 位 0101 0101 0101 即为 0 x 5 0x5 0x5,也需要 8 8 8 个 )故各需要 8 8 8 个 0 x A / 0 x 3 0xA/0x3 0xA/0x3,即为 0 x A A A A A A A A / 0 x 33333333 0xAAAAAAAA/0x33333333 0xAAAAAAAA/0x33333333。
int HammingWeight(unsigned int n)
{
//(n & 0x55555555)每相邻两位忽略高位保留低位为1的二进制序列,
//(n & 0xaaaaaaaa)>>1每相邻两位忽略低位保留高位为1的二进制序列并右移1位,高位补零。
//上面两个子序列相加,则为每相邻两位高位和对应低位为1的相加,往前一位进1。
//也就是检查每对相邻的2位有几个1
n = (n & 0x55555555) + ((n & 0xaaaaaaaa) >> 1);
//每相邻的四位有几个1
n = (n & 0x33333333) + ((n & 0xcccccccc) >> 2);
//每相邻的八位有几个1
n = (n & 0x0f0f0f0f) + ((n & 0xf0f0f0f0) >> 4);
//每相邻的十六位有几个1
n = (n & 0x00ff00ff) + ((n & 0xff00ff00) >> 8);
//32位有几个1
n = (n & 0x0000ffff) + ((n & 0xffff0000) >> 16);
return n;
}
int main()
{
int c = HammingWeight(16);
cout << c << endl;
}
在采用 H a m m i n g W e i g h t HammingWeight HammingWeight 方法时,对于任何一个 32 32 32 位无符号整数 N N N 只需要计算 5 5 5 次运算即可。
总结与应用
- H a m m i n g W e i g h t HammingWeight HammingWeight 使用了分治/递归的思想,将问题巧妙解决,降低了运算次数。
- 如果定义两个长度相等的 0 / 1 0/1 0/1 串中对应位不相同的个数为海明距离(即码距),则某 0 / 1 0/1 0/1 串和全 0 0 0 串的海明距离即为这个 0 / 1 0/1 0/1 串中 1 1 1 的个数。
- 两个 0 / 1 0/1 0/1 串的海明距离,即两个串异或值的 1 1 1 的数目,因此,该问题在信息编码等诸多领域有广泛应用。
跳跃问题
问题描述
给定非负整数数组,初始时在数组起始位置放置一机器人,数组的每个元素表示在当前位置机器人***最大能够跳跃的数目***。它的目的是用最少的步数到达数组末端。例如:给定数组 A = [ 2 , 3 , 1 , 1 , 2 ] A=[2,3,1,1,2] A=[2,3,1,1,2],最少跳步数目是 2 2 2,对应的跳法是: 2 − > 3 − > 2 2->3->2 2−>3−>2。
如: 2 , 3 , 1 , 1 , 2 , 4 , 1 , 1 , 6 , 1 , 7 2,3,1,1,2,4,1,1,6,1,7 2,3,1,1,2,4,1,1,6,1,7,最少需要几步?
问题分析
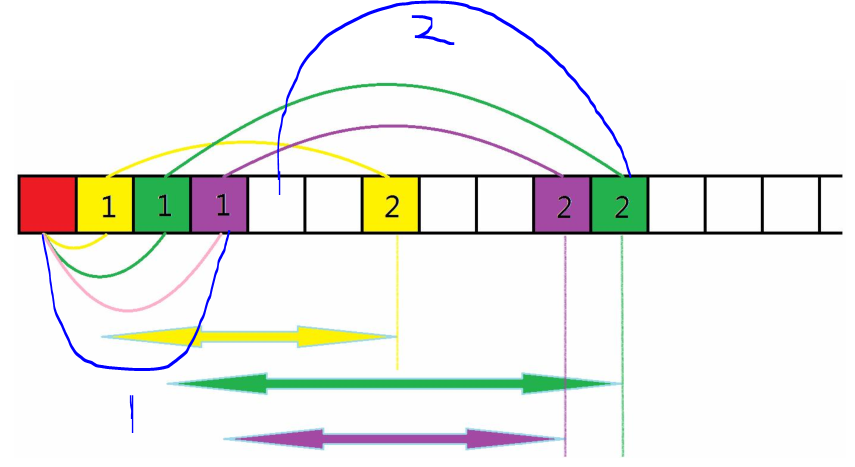
由上图我们可以看出当前跳的范围为蓝色的 1 1 1 范围,下一跳的范围为蓝色的 2 2 2 范围。
-
初始步数 s t e p step step 赋值为 0 0 0;
-
记当前步的控制范围是 [ i , j ] [i,j] [i,j],则用 k k k 遍历 i i i 到 j j j;
计算 A [ k ] + k A[k]+k A[k]+k 的最大值,记做 j 2 j2 j2; A [ k ] A[k] A[k] 表示当前位置最远能跳的距离。 -
s t e p + + step++ step++;继续遍历 [ j + 1 , j 2 ] [j+1,j2] [j+1,j2];
每一个 s t e p step step 都有当前可跳到的范围,而当前的范围又确定下一个 s t e p step step 的可跳到的范围。每在一个 s t e p step step 遍历当前可跳的范围,确定下一跳的范围。这样总可以找到最短的 s t e p step step 跳到终点。每一个 s t e p step step 可跳的范围内,其 s t e p step step 的值都是相同。这个解题过程类似于广度优先搜索。,每一个 s t e p step step 可跳的范围为一层。
实现代码
int Jump(int* a,int size)
{
if (size == 1)
return 0;
int i = 0;
int j = 0;//初始可跳的范围即为[i,j]
int k,j2;
int step = 0;
while (j<size)
{
step++;
j2 = j;
for (k = i; k <= j; k++)//遍历当前step可跳的范围来确定下一跳的范围
{
j2 = max(j2, k + a[k]);
if (j2 > size - 1)
return step;
}
i = j + 1;//上一跳的终点的下一个格子为下一跳的起点,注意a[k]为最大可跳的距离,最少可跳一步。
j = j2;//下一跳终点
if (j < i)
return -1;
}
return step;
}
Jump问题总结
虽然从代码上看有两层循环,但是我们分析执行过程可知只是从序列头跳到序列尾,时间复杂度只有 O ( n ) O(n) O(n)。
该算法在每次跳跃中,都是尽量跳的更远,并记录 j 2 j2 j2——属于***贪心法***;也可以认为是从区间 [ i , j ] [i,j] [i,j] (若干结点)扩展下一层区间 [ j + 1 , j 2 ] [j+1,j2] [j+1,j2] (若干子结点)——属于***广度优先搜索***。
错位排列问题
问题描述
1 1 1 到 n n n 的全排列中,第 i i i 个数不是 i i i 的排列共有多少种?
问题分析
- 假定 n n n 个数的错位排列数目为 d p [ n ] dp[n] dp[n]
- 先考察数字 n n n 的放置方法:显然, n n n 可以放在从 1 1 1 到 n − 1 n-1 n−1 的某个位置,共 n − 1 n-1 n−1 种方法;假定放在了第 k k k 位。
- 对于数字
k
k
k:
要么放置在第 n n n 位
要么不放置在第 n n n 位。
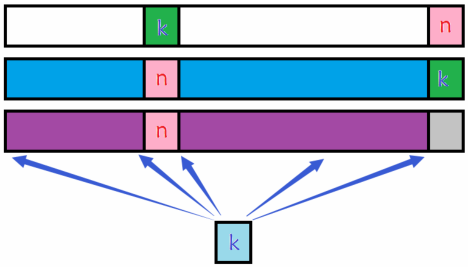
数字k放置在第n位
相当于数字 k k k 和数字 n n n 交互位置后,其他 n − 2 n-2 n−2 个数字做错位排列,因此有 d p [ n − 2 ] dp[n-2] dp[n−2] 种方法。

数字k不放置在第n位
将数字 k k k 暂时更名为 n n n (这是可以做到的:因为真正的 n n n 已经放在第 k k k 位上,真正的 n n n 不再考虑之列),现在需要将 1 1 1 到 k − 1 k-1 k−1 以及 k + 1 k+1 k+1 到 n n n 这 n − 1 n-1 n−1 个数放置在相应位置上,要求数字和位置不相同!显然是 n − 1 n-1 n−1 个数的错位排列,有 d p [ n − 1 ] dp[n-1] dp[n−1] 种方法。
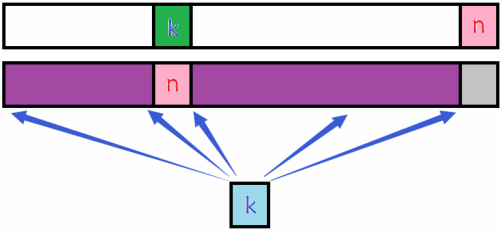
错位排列递推公式
综上, d p [ n ] = ( n − 1 ) ∗ ( d p [ n − 1 ] + d p [ n − 2 ] ) dp[n]=(n-1)*(dp[n-1]+dp[n-2]) dp[n]=(n−1)∗(dp[n−1]+dp[n−2]), ( n − 1 ) (n-1) (n−1) 表示起始时,数字 n n n 有 ( n − 1 ) (n-1) (n−1) 个可放置的位置。
初值
只有
1
1
1 个数字,错位排列不存在,
d
p
[
1
]
=
0
dp[1]=0
dp[1]=0;
只有
2
2
2 个数字,错位排列即交换排列,
d
p
[
2
]
=
1
dp[2]=1
dp[2]=1;
则递推公式为:

实现代码
int dislocationSorting(int n)
{
int* dp = new int[n];
dp--;
dp[1] = 0;
dp[2] = 1;
for (int i = 3; i <= n; i++)
dp[i] = (i - 1)*(dp[i - 1] + dp[i - 2]);
return dp[n];
}
int main()
{
int c = dislocationSorting(2);
cout << c << endl;
}





















 2186
2186











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








