CG-Orthogonal Range Searching

Orthogonal Range Searching -Querying a Database

(正交区域查找:数据库查询)

CG系列文章

---

CG-Introduction
CG-Voronoi Diagrams
CG-Line Segment Intersection
CG-Polygon Triangulation
CG-Delaunay Triangulations
CG-Orthogonal Range Searching
CG-windowing query

---

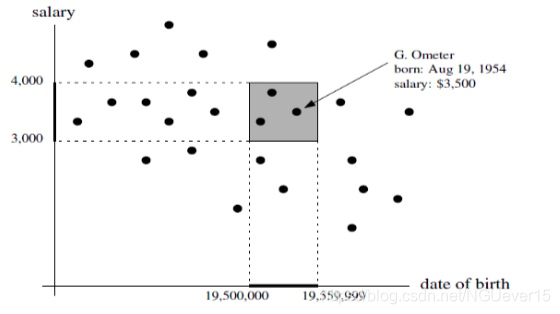
从几何的角度来理解对数据库的查询
我们将每位员工表 示为平面上的一个点:点的第一个坐标是出生日期，比如可以表示为一个整数，其值为 10,000 × 年 + 100 × 月 + 日;第二个坐标是月收入。

对数据库中“出生于 1950 年至 1955 年之间、月收入在$3,000 至$4,000 之间 的所有员工”的查询，就转化为一个几何查询:报告出第一个坐标介于 19,500,00 和 19,550,000 之间、 第二个坐标介于 3,000 到 4,000 之间的所有点。

给定一个与坐标轴平行的查询矩形，我们 希望找出落在其中的所有点

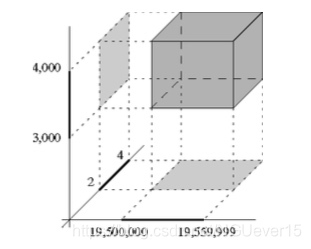
将数据库查询转化为空间的区域查找
每位员工表示为三维空间中的一个点:点的第一个坐标是出生日期; 第二个坐标是月收入;而第三个坐标则是孩子的数目。

5.1 1-Dimensional Range Searching

（一维区域查找）

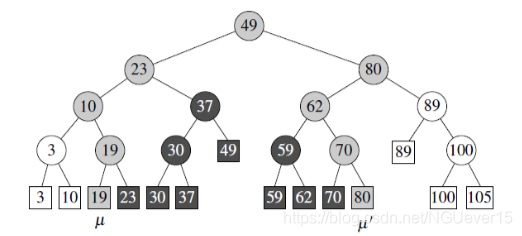
在二分查找树上的一维区域查找

**我们假设:**v 的左子树中存储了(坐标)不超过 xv 的所有点，而其 右子树中则存储了(坐标)严格大于 xv 的所有点。

找到x和x’ 对应的两条查找路径开始分叉的位置，记这个节点为vsplit.

FINDSPLITNODE(T,x,x)

if x’<xv 说明查询区域在当前v的左侧
else 说明查询区域在当前v的右侧

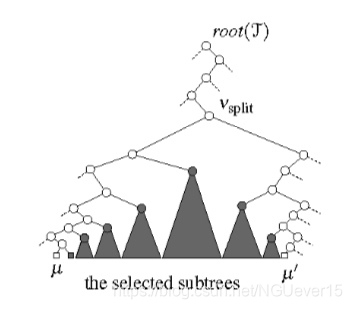
从vsplit出发分两路前进

Algorithm 1DRANGEQUERY(T,[x : x])

.jpg)
每向左前进一步，就枚举出该 处右子树中的所有叶子⎯⎯因为，这棵子树必然介于上述两条查找路径之间。
从vsplit出发 沿着x’对应的查找路径前进，并且每向右前进一步，都枚举出该处左子树中的所有叶子。
还要分别检查一下两条查找路径终点处的叶子，因为它们对应的点可能位于区间[x : x’]之内，也可 能位于其外。

Lemma 5.1

Algorithm 1DRANGEQUERY reports exactly those points that lie
in the query range.

算法 1DRANGEQUERY 所报告出来的，恰好就是落在查找区间内的所有点。

证明：
1）显示任何报告的点p都在查询范围内。
2）显示该范围内的任何点p都被报告

Theorem 5.2

Let P be a set of n points in 1-dimensional space. The set P can be stored in a balanced binary search tree, which uses O(n) storage and has O(nlogn) construction time, such that the points in a query range can be reported in time O(k + log n), where k is the number of reported points.

给定由一维空间中任意 n 个点构成的集合 P。可以使用 O(n)空间，在 O(nlogn)时间内构造一棵平衡二 分查找树以存储 P。这样，可以在 O(k + logn)时间内查找出任何区间内的所有点(其中，k 是实际被 查找出来的点数)。

5.2 Kd-Trees

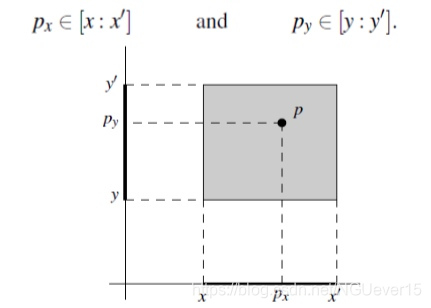
针对P的一次二维矩形区域查找，就是要从P中找出落在某一待查询矩形[x : x’] × [y : y’]之内的所有点。点p := (px, py)落在该矩形之内，当且仅当px ∈[x:x] and py ∈[y:y].

每次二维矩形区域查找，都可以分解为两次一维子查找.其中一次沿 x 方向进行，另一次沿 y 方向进行。

首先沿x坐标方向做一 次划分，然而沿y方向做一次，接着再次沿x方向划分，如此下去.

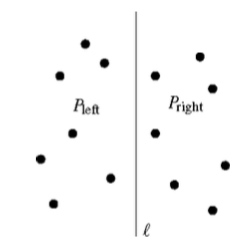
在根节点处，通过一条垂线l将集合P划分为大小接近的(左、右)两 个子集。

该分割线存储于根节点处。位于分割线左侧的那个子集记作Pleft，它被存储于左子树中;位于分 割线右侧的那个子集记作Pright，它被存储于右子树中。
在根节点的左孩子处，继续通过一条水平线， 将Pleft划分为(上、下)两个子集:位于该分割线以下或者落于其上的那些点，被存储于该左孩子的 左子树中;而位于分割线以上的那些点，则被存储于右子树中。

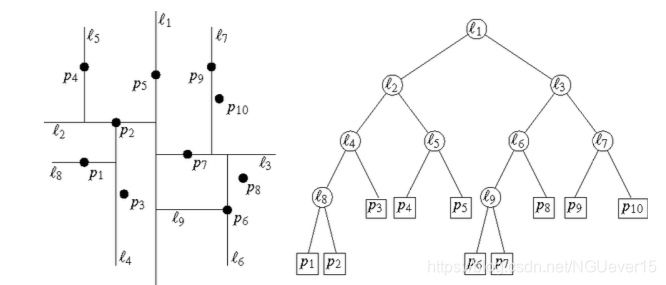
一棵kd-树:左侧所示的是对整个平面的一个划分，右侧为其对应的二分查找树(实际上是一颗2d-树)

Algorithm BUILDKDTREE(P,depth)

第一个参数就是我们需要为之建立 kd-树的点集;初次调用时，它就是集合 P 本身。
第二个参 数为递归深度，即在递归调用构造子程序时，对应子树根节点的深度。初次调用时，后一参数设置 为零。

depth为偶数时为垂直线
depth为奇数时为水平线

构造过程所需的时间 T(n)符合下列递推关系:

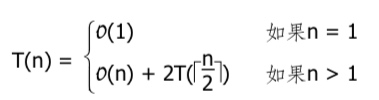
Lemma 5.3

A kd-tree for a set of n points uses O(n) storage and can be con- structed in O(nlogn) time.

给定由任意n个点组成的一个集合 1，其对应的kd-树占用O(n)空间，并可以在O(nlogn)时间内构造出来。

Query algorithm

一般而言，任一节点v所对应的子区域是一个矩形，不过，这个矩形在某些边的方向上可能 是无界的(unbounded)。
这个矩形之所以在某些方向是有界的，是由于受到了v的祖先们所对应的分割线的界定.

!
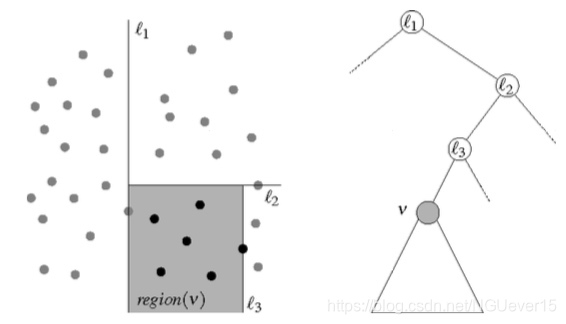
kd-树中各节点与平面上某一子区域的对应关系
我们将对应于节点v的子区域记为region(v)。显然，对应于kd-树根节点的区域就是整个平面。

上图中以v为根 的子树所存储的，就是黑色的点。
只有当region(v)与待查询区域相交时，我们才有必要对以v 为根的子树进行查找

**查找算法:**对kd-树做遍历(traversal)⎯⎯ 不过，只访问那些其对应子区域与查找矩形相交的节点。

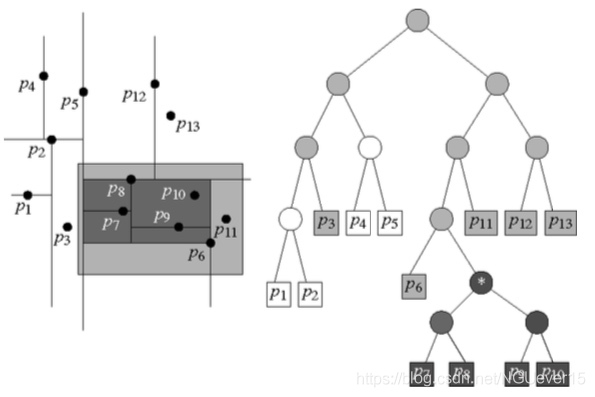
如果 待查询区域为其中的灰色矩形，那么其中灰色的那些节点将会被访问到。
那个标有星号的节点，对 应于一个完全包含于待查询区域之中的子区域。
其它被访问 到的叶子，需要对它们所对应的点进行测 试，以确定其是否落在待查询区域之内(p6 和p11 将会以这种方式被报告出来)。

lc(v)和rc(v)分别表示节点v的左、右孩子

给定处于偶数深度的某个节点v 所对应的子区域region(v)，其左孩子所对应的子区域可以这样获得:
region(lc(v)) = region(v) ∩ l(v)left
其中，l(v)就是存储于 v 处的分割线，而 l(v)left 则是 l(v)左侧(包含 l(v))的半平面。

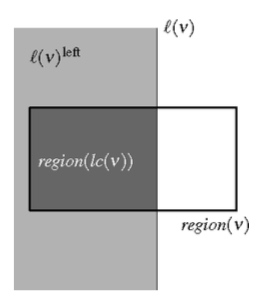
判断R是否与region(v)相交

Algorithm SEARCHKDTREE(ν,R)

[外链图片转存失败(img-vWBaOcxW-1565420475122)(media/15479805212299/]
在子树完全包含查询区域的时候，调用REPORTSUBTREE
在子树与查询区域相交的时候，调用SEARCHKDTREE
上述判断的四个条件，至少有一个是满足的。

Lemma 5.4

A query with an axis-parallel rectangle in a kd-tree storing n points can be performed in O(√n + k) time, where k is the number of reported points.

如果待查询区域为与坐标轴平行的矩形，那么对于存储了任意 n 个点的一棵 kd-树，每次查询都可以 在 O( n + k)时间内完成，其中 k 为实际被报告出来的点数。

Theorem 5.5

A kd-tree for a set P of n points in the plane uses O(n) storage and can be built in O(nlogn) time. A rectangular range query on the kd-tree takes O(√n + k) time, where k is the number of reported points.

给定由平面上任意 n 个点构成的集合 P，其对应的 kd-树将占用 O(n)空间，并且可以在 O(nlogn)时间 内构造出来。使用这棵 kd-树，每次矩形区域查找所需的时间将不会超过 O( n + k)，其中 k 为实际 被报告出来的点数。

5.3 Range Trees(区域树)

这种结构的查询时间性能更好，具体而言，是 O(log2n + k)。为实现这一改进，需要在其它方 面付出代价⎯⎯存储空间将由 kd-树的 O(n)，上升到区域树的 O(nlogn)。
用空间换时间

如果只关系x轴方向，可转化为一维查询问题
在这棵树中查找x和x’，直到我们到达某个节点vsplit，两条查找路 径在这里分道扬镳。

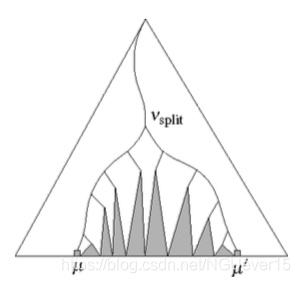
确定vsplit后，从这里分两路继续查找

正则子集：
在以v为根的子树中，各匹叶子所对应的点构成的(P的)一个子集，称作与v对应的正则子集。

对于P(v)中的所有点，我们都有一棵按照其y-坐标组织的二分 查找树

Definition of range tree

• 主树(maintree)是一棵平衡二分查找树T，按照P中各点的x-坐标，将它们组织起来
• 对于T中的每个内部节点或者叶子v，再将正则子集P(v)中的各点按照y-坐标，存储为一棵 平衡二分查找树 Tassoc(v)。节点 v 拥有一个指针，指向 Tassoc(v)的根。我们称 Tassoc(v)为 v 的联 合结构(associated structure)。

节点具有指向关联结构的指针的数据结构通常称为多级数据结构。
然后，主树被称为第一级树，相关结构是第二级树。
可以使用以下递归算法构造范围树。

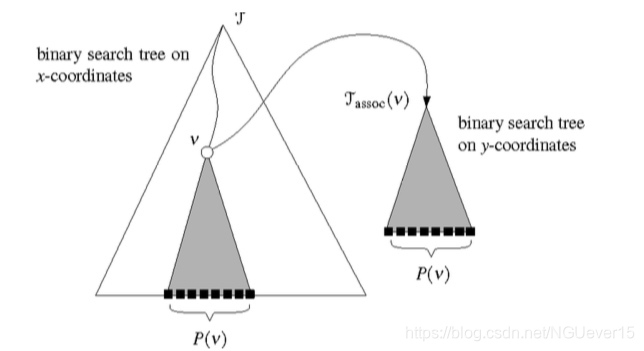
二维区域树

Algorithm BUILD2DRANGETREE§

设 xmid 为 P 中各点 x-坐标的中值
Pleft 由所有 x-坐标小于或者等于 xmid 的点组成 Pright 由所有 x-坐标大于 xmid 的点组成
生成一个节点 v 以存储 xmid
将 vleft 做为 v 的左孩子
将 vright 做为 v 的右孩子
将 Tassoc 做为 v 的联合结构

在联合结构的叶子内，不仅要存储其对应点的 y-坐标，而且要存储这些点本身。（因为需要把这些点报告出来）

Lemma 5.6

A range tree on a set of n points in the plane requires O(n log n) storage.

给定由平面上任意 n 个点构成的点集，其对应的区域树占用 O(nlogn)的存储空间。

Algorithm 2DRANGEQUERY(T,[x : x]×[y : y])

Lemma 5.7

A query with an axis-parallel rectangle in a range tree storing n points takes O(log2 n + k) time, where k is the number of reported points

若采用区域树来存储(平面上的)任意 n 个点，则与坐标方向平行的每一次矩形区域查询，只需要 O(log2n + k)时间。这里的 k 为实际被报告出来的点数。

Theorem 5.8

Let P be a set of n points in the plane. A range tree for P uses O(nlogn) storage and can be constructed in O(nlogn) time. By querying this range tree one can report the points in P that lie in a rectangular query range in O(log2 n + k) time, where k is the number of reported points

给定由平面上任意 n 个点构成的集合 P。对应于 P 的一棵区域树占用 O(nlogn)的存储空间，并且可以 在 O(nlogn)时间内构造出来。对这棵区域树进行查找，可以在 O(log2n + k)时间内，从 P 中报告出落 在任一矩形待查询区域之内的所有点，其中 k 为实际被报告出来的点数。

5.4 Higher-Dimensional Range Trees

(高维的区域查询树)

第一层次的这棵树也就是主树，对于其中的任一节点v，在以v为根节点的子树中，所有叶子各自对 应的点，合起来构成了与v对应的正则子集P(v)。
第二层次的每棵树Tassoc(v)，都是对应于P(v)中某个点的一棵(d-1)维区域树。
它将是按照各点 第二维坐标组织的一棵平衡二分查找树，其中各个节点都通过一个指针，指向一棵(d-2)维区域树， 这棵区域树存储了该节点的子树 2中的所有点

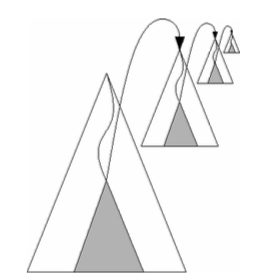
在高维区域树中逐层查找

Theorem 5.9

Let P be a set of n points in d-dimensional space, where d 2. A range tree for P uses O(nlogd−1n) storage and it can be constructed in O(nlogd−1 n) time. One can report the points in P that lie in a rectangular query range in O(logd n + k) time, where k is the number of reported points.

给定由 d 维空间中任意 n 个点构成的集合 P，d ≥ 2。对应于 P 的一棵区域树占用 O(nlogd-1n)的存储空间，并且可以在 O(nlogd-1n)时间内构造出来。对这棵区域树进行查找，可以在 O(logdn + k)时间内， 从 P 中报告出落在给定(超)矩形待查询区域之内的所有点，其中 k 为实际被报告出来的点数。

5.5 General Sets of Points

对应于 a 和 b 两个实数的合成数，记作(a|b)。
按照字典 序(lexicographical order)，我们可以在合成数空间中定义一个全序(total order)。这样，对于任何 两个合成数(a|b)和(a’|b’)，都有

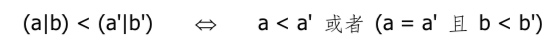
我们将每个点 p := (px, py)，替换为一个以合成数为坐标的点 ^p:= ((px|py), (py|px))。

现在假设我们希望报告出 P 中位于 R := [x : x’] × [y : y’]之内的所有点。为此，必须对刚才为 ^ P构 造的树进行查找。也就是说，必须同时将待查询区域也变换到新的合成数空间。这一变换定义如下:

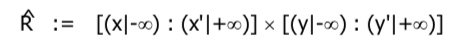
Lemma 5.10

Let p be a point and R a rectangular range. Then

对于任意的一个点 p 以及一个矩形区域 R，都满足上述公式。

观察不需要实际存储变换点：只要我们在复合空间中对两个x坐标或两个y坐标进行比较，我们就可以存储原始点。

5.6* Fractional Cascading

（分散层叠）
如果A1[i]所存储对象的关键码为yi，那么我们为它配备的指针，将指向A2 中不小于yi的最小关键码。 若A2 中没有这样一个关键码，则将A1[i]对应的这个指针置为nil。

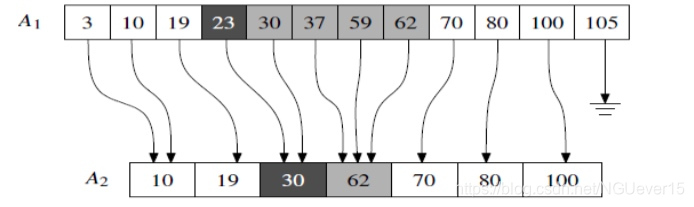
增加指针以加速查找
在 A1 中对 y 进行二分查找，然后沿着 A1 朝右方前行，直到第一个大于 y’的关键码。

最重要的一个观察结果就是:正则子集 P(lc(v))和 P(rc(v))都是 P(v)的子 集。

我们不再像第 5.3 节那样将联合结构组织成一棵二分查找树，而是组织成一个数组 A(v)。 每一数组都按照 y-坐标排序。此外，A(v)中的每一元素都配有两个指针，分别指向 A(lc(v))和 A(rc(v))。

这两个指针的设置方法如下：
假设在 A(v)[i]处存储的是点 p。于是，我们为 A(v)[i]设 置一个指针，指向 A(lc(v))中的一个元素，该元素所存储的点 p’的 y-坐标，(在 A(lc(v))中)是不小 于 py 的最小者。正如上面所指出的，P(lc(v))是 P(v)的一个子集。因此，若在 P(v)所存储的诸点中， p 的 y-坐标是不小于某一 y 值的最小者，则在 P(lc(v))所存储的诸点中，p’的 y-坐标也是不小于 y 的 最小者。指向 A(rc(v))的指针的设置方法相同:在 A(rc(v))所存储的诸点中，该指针所指(位置处所 存储)的那个点，其 y-坐标是不小于 py 的最小者。

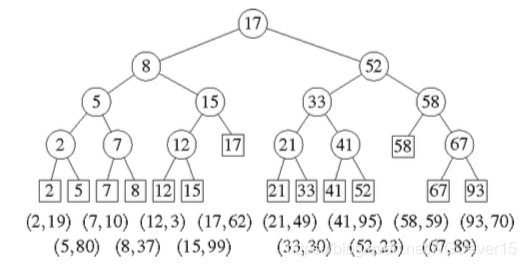
做过上述改动之后的区域树，称作层次化区域树;

下图分别对应于上图在(主)树中所关联节点的位置:最顶层的 那个数组对应于根节点;其下面的左侧的那个数组对应于根节点的左孩子;

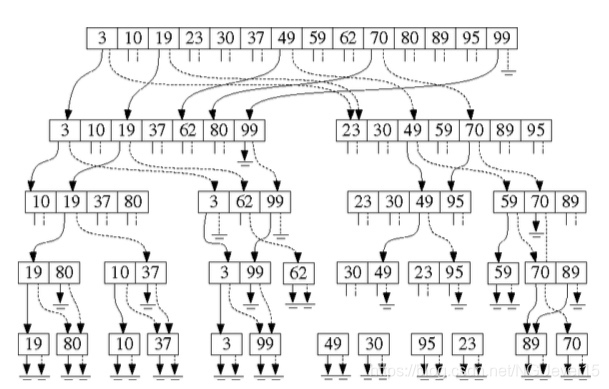
与主树中各节点相关联的数组:各数组所对应正则子集中的诸点，都按照y-坐 标排序(这里并没有画出所有的指针)

两个子数组内容是由树状结构中的点击对应的正则子集决定的，不管是左数组还是右数组，都指向第一个不小于自己的数

Theorem 5.11

Let P be a set of n points in d-dimensional space, with d 2. A layered range tree for P uses O(nlogd−1 n) storage and it can be constructed in O(nlogd−1 n) time. With this range tree one can report the points in P that lie in a rectangular query range in O(logd−1 n + k) time, where k is the number of reported points.

在 d(≥2)维空间中，给定由任意 n 个点构成的集合 P。总可以在 O(nlogd-1n)时间内，构造出一棵与 P 对应的层次化区域树，其占用的存储空间为 O(nlogd-1n)。借助于这棵区域树，可以在 O(logd-1n + k)时 间内，报告出 P 中落在某矩形待查询区域之内的所有点，其中 k 为实际被报告出来的点数。