java实现二叉树的构建以及3种遍历方法

二叉树的遍历
二叉树的遍历有三种方式，如下：
（1）前序遍历（DLR），首先访问根结点，然后遍历左子树，最后遍历右子树。简记根-左-右。
（2）中序遍历（LDR），首先遍历左子树，然后访问根结点，最后遍历右子树。简记左-根-右。
（3）后序遍历（LRD），首先遍历左子树，然后遍历右子树，最后访问根结点。简记左-右-根。
引用自：http://ocaicai.iteye.com/blog/1047397
1.树的构建方法

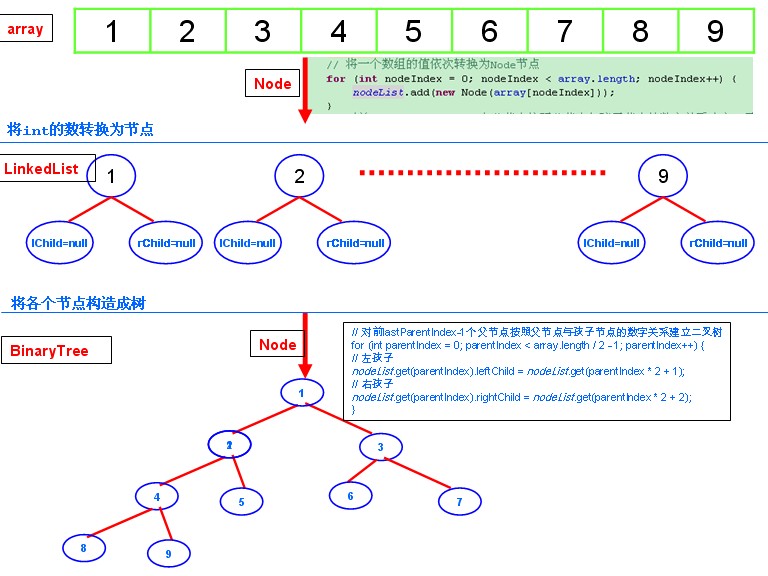
2.具体代码实现：

import java.util.LinkedList;
import java.util.List;

public class BinaryTree {
    private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };//数组长度至少为2
    private static List<Node> nodeList = null;

    // 静态内部类
    /*
     * The binary tree is built using this nested node class. Each node stores
     * one data element, and has left and right sub-tree pointer which may be
     * null. The node is a "dumb" nested class -- we just use it for storage; it
     * does not have any methods.
     */
    @SuppressWarnings("unused")
    private static class Node {
        Node leftChild;
        Node rightChild;
        int data;

        Node(int newData) {
            leftChild = null;
            rightChild = null;
            data = newData;
        }
    }

    /**
     * 
     * @description 初始化二叉树，把一个数组的值赋给一个二叉树
     * 
     */
    public void createBinaryTree() {
        nodeList = new LinkedList<BinaryTree.Node>();
        // 将数组中的值一次转换为Node节点，其left，right初始化为null
        for (int nodeIndex = 0; nodeIndex < array.length; nodeIndex++) {
            nodeList.add(new Node(array[nodeIndex]));
        }
        // 最后一个父节点的索引
        int lastParentIndex = array.length / 2 - 1;
        // 对前lastParentIndex-1个父节点按照父节点与孩子节点的数字关系建立二叉树
        /*
         * 关系分析： 
         *       数组下标：012345678 
         *       列举法： 
         *       数组下标是0(data=1) leftChild：数组下标1（data=2） rightChild:数组下标2（data=3）
         *       数组下标是1(data=2) leftChild：数组下标3（data=4） rightChild:数组下标4（data=5）
         *       数组下标是2(data=3) leftChild：数组下标5（data=6） rightChild:数组下标6（data=7）
         *       数组下标是3(data=4) leftChild：数组下标7（data=8） rightChild:数组下标8（data=9）
         *        。。。
         *       数组下标是n         leftChild:数组下标是2n+1       rightChild:数组下标是2n+2
         *       
         */
        for (int parentIndex = 0; parentIndex < lastParentIndex; parentIndex++) {
            // 设置左孩子节点
            nodeList.get(parentIndex).leftChild = nodeList
                    .get(parentIndex * 2 + 1);
            // 设置右孩子节点
            nodeList.get(parentIndex).rightChild = nodeList
                    .get(parentIndex * 2 + 2);
        }
        // 最后一个父节点:因为最后一个父节点可能没有右孩子，所以单独拿出来处理  
        // 左孩子  
        nodeList.get(lastParentIndex).leftChild = nodeList  
                .get(lastParentIndex * 2 + 1);  
        // 右孩子,如果数组的长度为奇数才建立右孩子  
        if (array.length % 2 == 1) {  
            nodeList.get(lastParentIndex).rightChild = nodeList  
                    .get(lastParentIndex * 2 + 2);  
        }  
    }
    /**
     *      
     * @description     先序遍历
     * @param node      遍历开始的节点
     *      
     *
     */
    public static void preOrderTraverse(Node node){
        if(node==null){
            return;
        }
        //先打印根节点
        System.out.print(node.data);
        if(node.leftChild!=null){
            preOrderTraverse(node.leftChild);
        }
        if(node.rightChild!=null){
            preOrderTraverse(node.rightChild);
        }
    }
    /**
     *      
     * @description     中序遍历
     * @param node      
     *      
     */
    public static void inOrderTraverse(Node node){
        if(node==null){
            return;
        }
        if(node.leftChild!=null){
            inOrderTraverse(node.leftChild);
        }
        //打印根节点
                System.out.print(node.data);
        if(node.rightChild!=null){
            inOrderTraverse(node.rightChild);
        }
    }

    /**
     *      
     * @description     后序遍历
     * @param node      
     *      
     */
    public static void postOrderTraverse(Node node){
        if(node==null){
            return;
        }
        if(node.leftChild!=null){
            postOrderTraverse(node.leftChild);
        }
        if(node.rightChild!=null){
            postOrderTraverse(node.rightChild);
        }
        //打印根节点
        System.out.print(node.data);
    }



    public static void main(String[] args) {
        BinaryTree bt=new BinaryTree();
        bt.createBinaryTree();
        // nodeList中第0个索引处的值即为根节点  
        Node root = nodeList.get(0);  
        System.out.println("pre order:");
        BinaryTree.preOrderTraverse(root);
        System.out.println(); 

        System.out.println("in order:");
        BinaryTree.inOrderTraverse(root);
        System.out.println(); 

        System.out.println("post order:");
        BinaryTree.postOrderTraverse(root);
    }
}

3：输出:

pre order:
124895367
in order:
849251637
post order:
894526731