论文阅读：Wasserstein GAN

贡献：

• 彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度
• 基本解决了collapse mode的问题，确保了生成样本的多样性
• 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高
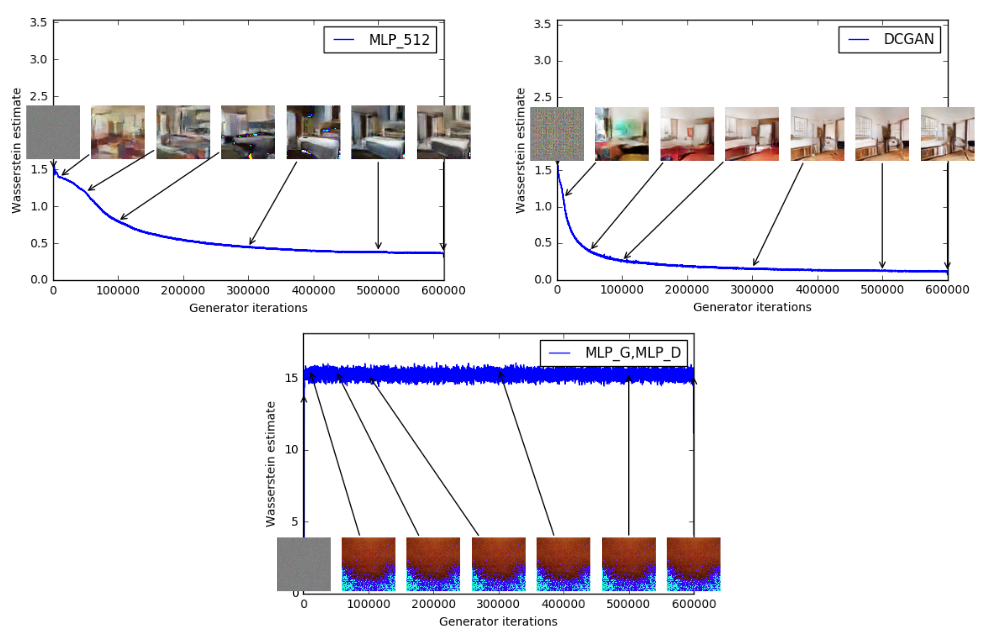
• 以上一切好处不需要精心设计的网络架构，最简单的多层全连接网络就可以做到

改进：

• 判别器最后一层去掉sigmoid
• 生成器和判别器的loss不取log
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
• 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

1. 原始GAN的问题

---

1.1 判别器越好，生成器梯度消失越严重

---

原始GAN训练有一个trick，就是别把判别器训练得太好，否则在实验中生成器会完全学不动（loss降不下去）。

根据原始GAN定义的判别器loss，可以得到最优判别器的形式；而在最优判别器的下，可以把原始GAN定义的生成器loss等价变换为最小化真实分布Pr与生成分布Pg之间的JS散度。
越训练判别器，它就越接近最优，最小化生成器的loss也就会越近似于最小化Pr和Pg之间的JS散度。
如果两个分布之间越接近，它们的JS散度越小，通过优化JS散度就能将Pg拉向Pr，最终以假乱真。

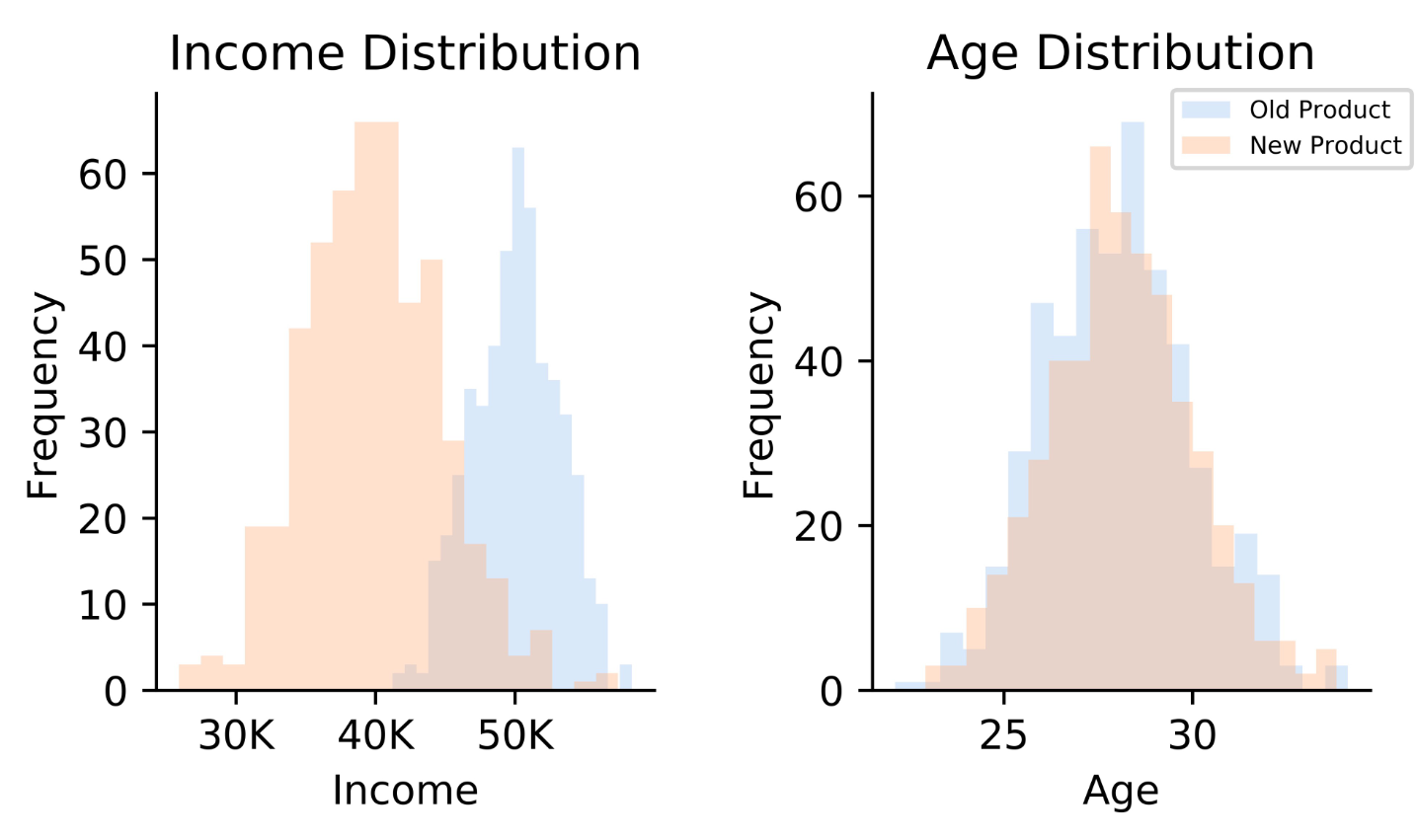
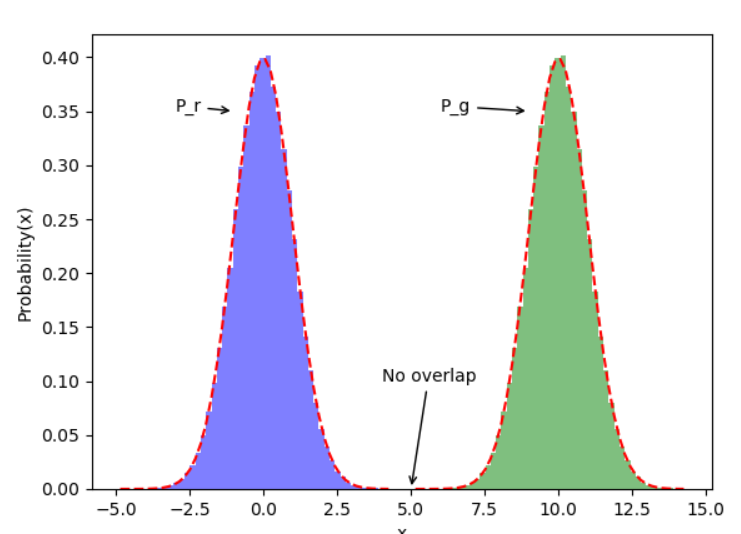
如果两个分布完全没有重叠的部分，或者它们重叠的部分可忽略，JS散度就固定是常数log⁡2，而这对于梯度下降方法意味着——梯度为0，梯度消失。

当Pr与Pg的支撑集（support）是高维空间中的低维流形（manifold）时，Pr与Pg重叠部分测度（measure）为0的概率为1。

• 支撑集（support）其实就是函数的非零部分子集，比如ReLU函数的支撑集就是(0,+∞)，一个概率分布的支撑集就是所有概率密度非零部分的集合。
• 流形（manifold）是高维空间中曲线、曲面概念的拓广，我们可以在低维上直观理解这个概念，比如我们说三维空间中的一个曲面是一个二维流形，因为它的本质维度（intrinsic dimension）只有2，一个点在这个二维流形上移动只有两个方向的自由度。同理，三维空间或者二维空间中的一条曲线都是一个一维流形。
• 测度（measure）是高维空间中长度、面积、体积概念的拓广，可以理解为“超体积”。
  因为一开始生成器随机初始化，所以Pg几乎不可能与Pr有什么关联，所以它们的支撑集之间的重叠部分要么不存在，要么就比Pr和Pg的最小维度还要低至少一个维度，故而测度为0。所谓”重叠部分测度为0“，就是“不重叠或者重叠部分可忽略”的意思。

结论：在（近似）最优判别器下，最小化生成器的loss等价于最小化Pr与Pg之间的JS散度，而由于Pr与Pg几乎不可能有不可忽略的重叠，所以无论它们相距多远JS散度都是常数log⁡2，最终导致生成器的梯度（近似）为0，梯度消失。

1.2 最小化第二种生成器loss函数，会等价于最小化一个不合理的距离衡量

---

导致两个问题，一是梯度不稳定，二是collapse mode即多样性不足。

公式推导后发现：等价最小化目标存在两个严重的问题。
第一，它同时要最小化生成分布与真实分布的KL散度，却又要最大化两者的JS散度，一个要拉近，一个却要推远！这在直观上非常荒谬，在数值上则会导致梯度不稳定，这是后面那个JS散度项的毛病。
第二，即便是正常的KL散度项也有毛病。 第一种错误对应的是“生成器没能生成真实的样本”，惩罚微小；第二种错误对应的是“生成器生成了不真实的样本” ，惩罚巨大。第一种错误对应的是缺乏多样性，第二种错误对应的是缺乏准确性。于是，生成器宁可多生成一些重复但是很“安全”的样本，也不愿意去生成多样性的样本，因为那样一不小心就会产生第二种错误，得不偿失。这种现象就是常说的collapse mode。

1.3 小结

---

在原始GAN的（近似）最优判别器下，第一种生成器loss面临梯度消失问题，第二种生成器loss面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚不平衡导致mode collapse这几个问题。

2. 前作解决方案

---

原始GAN问题的根源可以归结为两点：
一是等价优化的距离衡量（KL散度、JS散度）不合理；
二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。

前作针对第二点提出了一个解决方案：
对生成样本和真实样本加噪声，直观上说，使得原本的两个低维流形“弥散”到整个高维空间，强行让它们产生不可忽略的重叠。而一旦存在重叠，JS散度就能真正发挥作用，此时如果两个分布越靠近，它们“弥散”出来的部分重叠得越多，JS散度也会越小而不会一直是一个常数，于是梯度消失的问题就解决了。
在训练过程中，对所加的噪声进行退火（annealing），慢慢减小其方差，到后面两个低维流形“本体”都已经有重叠时，就算把噪声完全拿掉，JS散度也能照样发挥作用，继续产生有意义的梯度把两个低维流形拉近，直到它们接近完全重合。

加噪方案是针对原始GAN问题的第二点根源提出的，解决了训练不稳定的问题，不需要小心平衡判别器训练的火候，可以放心地把判别器训练到接近最优，但是仍然没能够提供一个衡量训练进程的数值指标。

本作就从第一点根源出发，用Wasserstein距离代替JS散度，同时完成了稳定训练和进程指标的问题。

3. Wasserstein距离

---

Wasserstein距离又叫Earth-Mover（EM）距离。
公式如下：
$$W(P_r,P_g)=\underset{\gamma \in \Gamma (P_r,P_g)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$

• $W(P_r,P_g)$：表示真实分布PrP_rPr​与生成分布PgP_gPg​之间的Wasserstein距离。
• ${\inf }_{\gamma \in \Gamma (P_r,P_g)}$：表示在所有可能的联合分布$\gamma$中，寻找使得距离最小的情况。这里的联合分布是指同时考虑两个分布的样本。
• ${\mathbb{E}}_{(x,y)\sim \gamma }$：表示对联合分布$\gamma$下的样本$(x,y)$的期望。
• $\Vert x-y\Vert$：表示样本点之间的距离，通常使用欧几里得距离。

这个公式的核心思想是，通过最小化从真实分布到生成分布的“运输成本”，来量化这两个分布之间的差异。

直观上可以把${\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$理解为在γ这个“路径规划”下把Pr这堆“沙土”挪到Pg“位置”所需的“消耗”，而W(Pr,Pg)就是“最优路径规划”下的“最小消耗”，所以才叫Earth-Mover（推土机）距离。

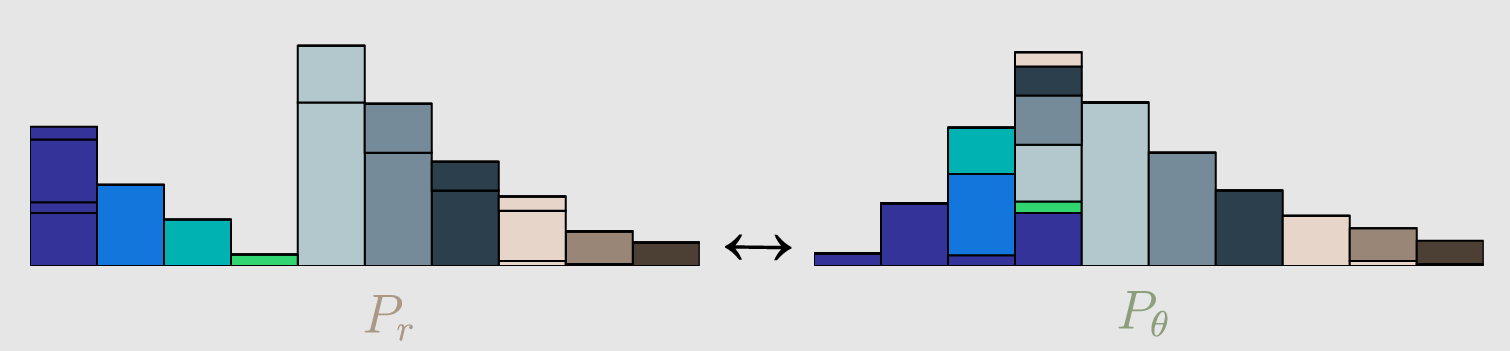
Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布没有重叠，Wasserstein距离仍然能够反映它们的远近。

Wasserstein距离是平滑的，梯度是有意义的。

4. WGAN

---

Wasserstein距离定义中的${\inf }_{\gamma \in \Gamma (P_r,P_g)}$没法直接求解，论文用了一个已有的定理把它变换为如下形式：
$$W(P_r,P_g)=\frac{1}{K}\underset{\Vert f{\Vert }_L\le 1}{\sup }{\mathbb{E}}_{x\sim P_r}[f(x)]-{\mathbb{E}}_{x\sim P_g}[f(x)]$$

• $W(P_r,P_g)$：表示真实分布$P_r$​与生成分布$P_g$​之间的Wasserstein距离。
• $\frac{1}{K}$：是一个常数，通常用于归一化。
• ${\sup }_{\Vert f{\Vert }_L\le 1}$：表示在所有满足某种约束（通常是Lipschitz连续性）的函数f中寻找上界。
• ${\mathbb{E}}_{x\sim P_r}[f(x)]$和${\mathbb{E}}_{y\sim P_g}[f(x)]$分别表示在真实分布和生成分布下的期望值。

理解为：在要求函数f的Lipschitz常数||f||L不超过K的条件下，对所有可能满足条件的f取到Ex∼Pr[f(x)]−Ex∼Pg[f(x)]的上界，然后再除以K。

可以用一组参数w来定义一系列可能的函数fw：
$$K\cdot W(P_r,P_g)\approx \underset{w:\Vert f{\Vert }_L<K}{\max }\left({\mathbb{E}}_{x\sim P_r}[f(x)]-{\mathbb{E}}_{x\sim P_g}[f(x)]\right)$$
理解为：把f用一个带参数w的神经网络来表示。

限制神经网络fθ的所有参数wi的不超过某个范围[−c,c]。

于是，可以构造一个含参数w、最后一层不是非线性激活层的判别器网络fw，在限制w不超过某个范围的条件下，使得
$$L={\mathbb{E}}_{x\sim P_r}[f(u(x))]-{\mathbb{E}}_{x\sim P_g}[f(w(x))]$$
尽可能取到最大，此时L就会近似真实分布与生成分布之间的Wasserstein距离（忽略常数倍数K）。

原始GAN的判别器做的是真假二分类任务，所以最后一层是sigmoid，但是现在WGAN中的判别器fw做的是近似拟合Wasserstein距离，属于回归任务，所以要把最后一层的sigmoid拿掉。

生成器要近似地最小化Wasserstein距离，可以最小化L，由于Wasserstein距离的优良性质，不需要担心生成器梯度消失的问题。再考虑到L的第一项与生成器无关，就得到了WGAN的两个loss。

算法流程：

5. 总结

---

分析原始GAN两种问题：

1. 由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性，使得生成器面临梯度消失的问题；
2. 在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度，又要最大化其JS散度，相互矛盾，导致梯度不稳定；KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性，导致collapse mode现象。

前作过渡方案：添加噪声

本作贡献：

• 引入Wasserstein距离，具有优越的平滑特性，理论上可以解决梯度消失问题；
• 将Wasserstein距离写成可求解的形式，可以近似Wasserstein距离；
• 在此近似最优判别器下优化生成器使得Wasserstein距离缩小，就能有效拉近生成分布与真实分布。

WGAN 从 GAN 的理论上深度剖析了 经典GAN loss 的劣势，并提出了释放GAN学习能力的方法， 重新用 Earth-Mover (EM) distance 或者说是 Wasserstein (W) distance 释放GAN的学习力，取得了非常好的效果。

参考资料

---

令人拍案叫绝的Wasserstein GAN