对于级数的概念,可以参考《泰勒级数及其应用》。在《高等数学》中,我们学习了傅立叶级数。傅立叶级数要求函数是周期的。对于非周期的函数,《复变函数与积分变换》中提出了傅立叶变换,使得傅立叶定理的适用范围更加大。前面的傅立叶级数和傅立叶变换都是针对连续函数,对于离散的情况,《数字图像处理与分析》中提出了离散傅立叶变换,使得傅立叶变换在图像处理中的得到广泛的应用。
傅立叶级数:法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),后世称为傅里叶级数(法文:série de Fourier,或译为傅里叶级数)一种特殊的三角级数。
三角级数是任何具有下述形式的级数:

当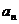
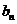
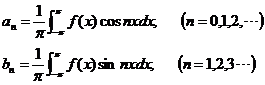
或者
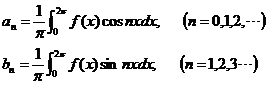
其中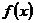
傅立叶级数的存在性:一个定义在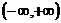
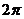
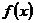
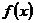
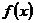
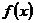
傅立叶级数收敛定理(Dirichlet定理):设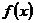
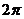
(1)在一个周期内连续,或者只有有限个第一类间断点,
(2)在一个周期内至多只有有限个极值点,
则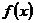
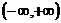
(1)当x是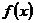
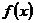
(2)当x是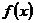
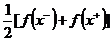
上面讨论的函数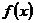
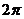
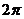
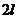
在《高等数学》中指出,只要作变量代换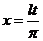
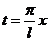
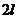
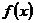
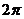
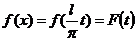
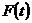
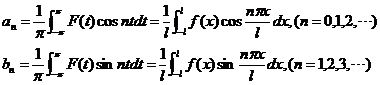
其实,在《复变函数与积分变换》中,指出了更为一般的形式:
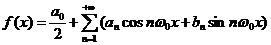
其中
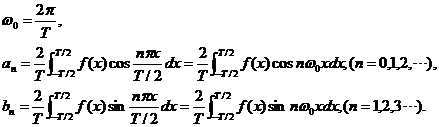
傅立叶级数复指数形式:在前面的讨论中,使用的都是三角函数的形式。在《复变函数与积分变换》中,给出了傅立叶级数的另外一种形式——复指数形式。通过复指数形式,可以将傅立叶级数推导至傅立叶变换。
欧拉公式如下所示:
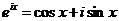
根据公式(7),可得:
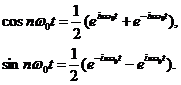
将式(8)代入式(5)得:
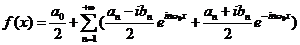
令
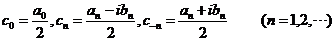
得
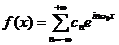
其中,根据式(10)可以得:
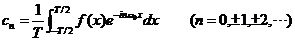
傅立叶级数工程应用:
在工程应用中,通常使用时间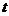
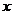
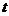
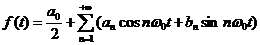
为了使得物理意义更加明显,令
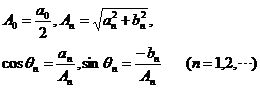
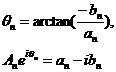
则式(13)改变为
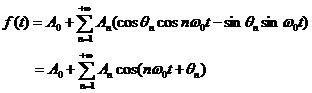
同理,将式(12))的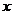
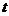
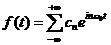
傅立叶级数物理意义:
式(16)说明,周期信号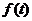
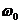
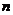
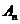
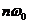
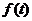
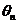
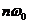
在《电路》的非正弦周期电流、电压、信号等的分析中,常常将其展开为傅立叶级数,也就是进行谐波分析。在《电路》中,将式(16)第一项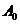
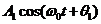
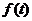
在《电路》中还指出,以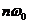
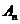
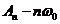
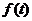
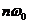
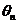
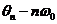
另外需要注意的是,时间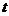
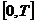
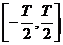
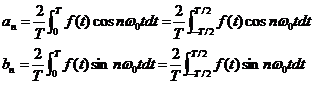
对于复指数形式,
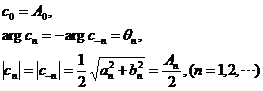
因此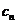
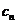
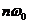
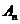
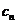
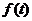
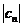
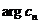
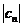
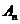
实例分析1
设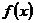
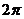
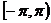
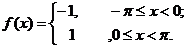
解:
由于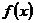
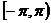
根据式(2)得
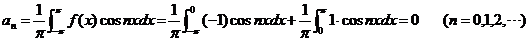
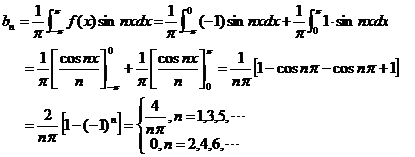
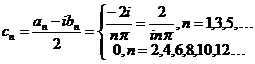
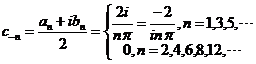
从而,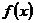
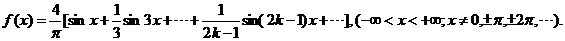
复指数形式为
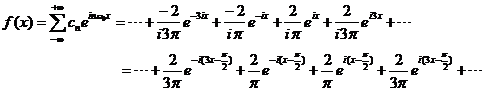
Matlab编程1:由于Matlab中没有专门的傅立叶级数函数,因此需要自己编程实现,如下所示。
%求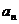
function an=fourieran(f,T,n)
syms x
w=2*pi/T;
an=2*int(f*cos(n*x),x,-T/2,T/2)/T;
%求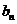
function bn=fourierbn(f,T,n)
syms x
w=2*pi/T;
bn=2*int(f*sin(n*w*x),x,-T/2,T/2)/T;
%求式(6)傅立叶级数展开的前15项
clear
clc
syms x n
f=x/abs(x); %式(13)的一种委婉表达
T=2*pi;
a0=fourieran(f,2*pi, 0); %先求a0,再求a1~a15
for n=1:15
a(n)=fourieran(f,T, n);
end
for n=1:15 %求b1~b15
b(n)=fourierbn(f,T, n);
end
求得结果:
a0=0
a=[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
b=[ 4/pi, 0, 4/(3*pi), 0, 4/(5*pi), 0, 4/(7*pi), 0, 4/(9*pi), 0, 4/(11*pi), 0, 4/(13*pi), 0, 4/(15*pi)]
结果分析:对比Matlab程序的运行结果和式(25),发现两者系数是一致的。这说明Matlab编程正确。
说明:本程序适合周期为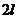
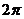
实例分析2
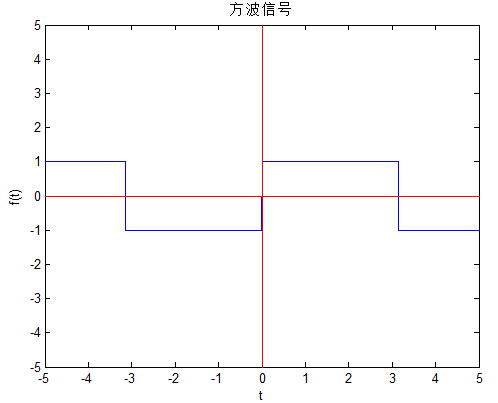
将实例分析1的函数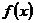
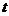
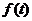
图1 方波函数
在实例分析1中,已经计算出了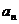
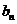
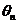
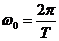
Matlab编程2
clear
clc
syms x n
% f=x^2+x^3
f=x/abs(x);
T=2*pi;
w0=2*pi/T;
t=[-5:0.01:5];
a0=fourieran(f,2*pi, 0);
for n=1:15
a(n)=fourieran(f,T, n);
end
for n=1:15
b(n)=fourierbn(f,T, n);
end
%计算相位
for n=1:15
g(n)=-atan(b(n)/a(n)); %由于b(n)/a(n)<0,因此g取负值,在前面加“-”。
end
%计算振幅
for n=1:15
A(n)=sqrt(a(n)*a(n)+b(n)*b(n));
end
figure(1)
f=A(1)*cos(1*w0*t+g(1))*0;
for n=1:2:15
fn=A(n)*cos(n*w0*t+g(n));
f=f+fn;
plot(t,fn);
hold on;
end
plot(t,f,'r');
% t=[-5:0.01:5];
hold on
plot(t,square(t));
plot(t,0,'k');
hold on
plot(0,t,'k');
set(gcf,'color','w');
xlabel('t')
ylabel('f(t)')
title('15次谐波合成曲线')
figure(2)
subplot(1,2,1);
bar(double(A))
title('幅度频谱')
ylabel('An');
xlabel('nw0');
subplot(1,2,2);
bar(double(g))
title('相位频谱')
ylabel('g');
xlabel('nw0');
set(gcf,'color','w');
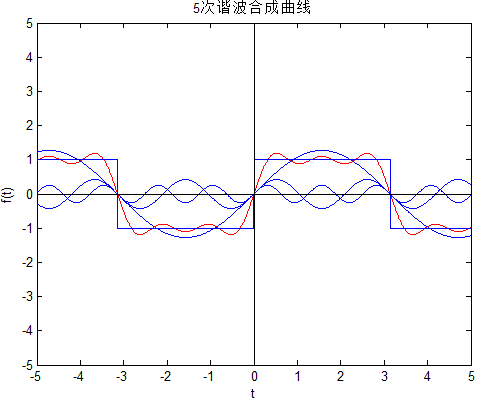
运行程序,得到图2、图3的结果:
图2 5次谐波合成曲线
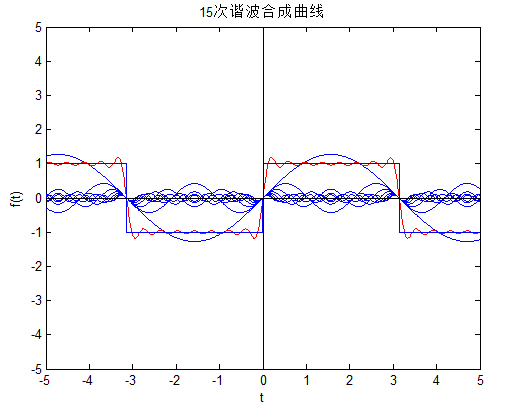
图3 15次谐波合成曲线
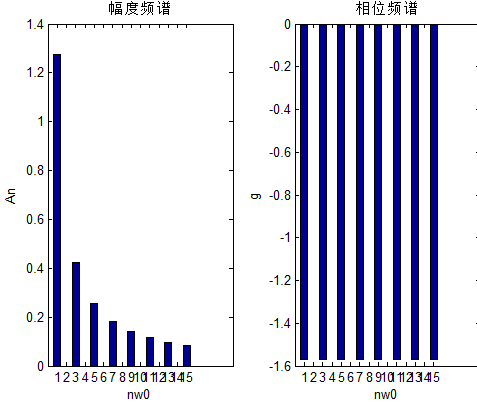
图4 矩形波频谱
在前面,我们讨论了周期函数的傅立叶级数,那么非周期函数应该怎样展开呢?
对于非周期函数,虽不能进行傅立叶级数展开,但是可以进行傅立叶变换!
为了表示周期函数与非周期函数的区别,用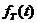
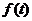
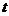
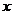
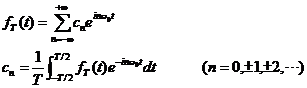
将非周期函数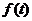
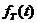
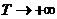
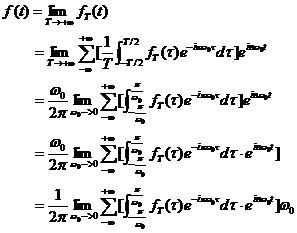
令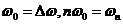
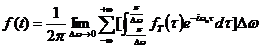
这是一个和式的极限,按照积分的定义,在一定条件下,式(29)可写为
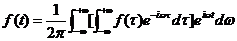
注意: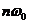
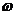
傅立叶积分定理:如果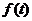
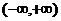
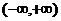
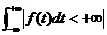
令式(30)中间的积分为
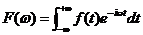
将式(31)代入式(30),得
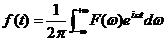
式(31)和式(32)就是传说中的傅立叶变换和傅立叶反变换!
傅立叶变换物理意义:
对比式(32)和式(27),由于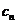
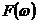
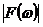
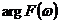
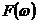
说明:由于式(32)和式(27)都是复数形式,因此其物理意义不明显,但是他们都是直接或者间接的源于式(16),因此具体的物理意义还要看回式(16)。通常我们需要求的是式(31),但它是一个复数结果,如果不明白它的物理意义,那么就不知如何对得到的结果进行合理的分析。
在《数字图像处理与分析》一书中,还提出了如下的傅立叶变换与反变换形式:
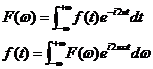
此外,还将一维函数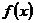
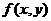
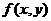
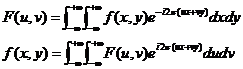
实例分析3
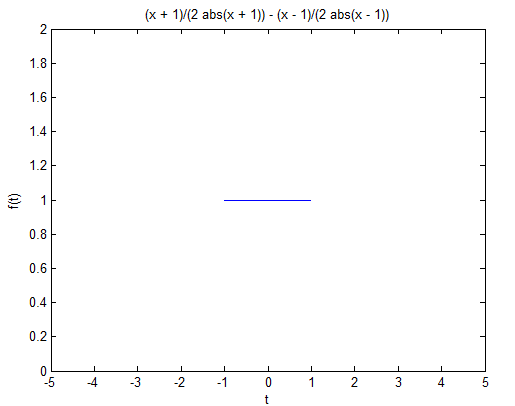
求矩形脉冲函数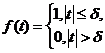
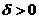
解:
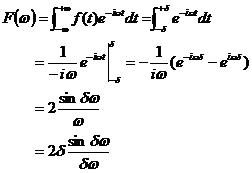
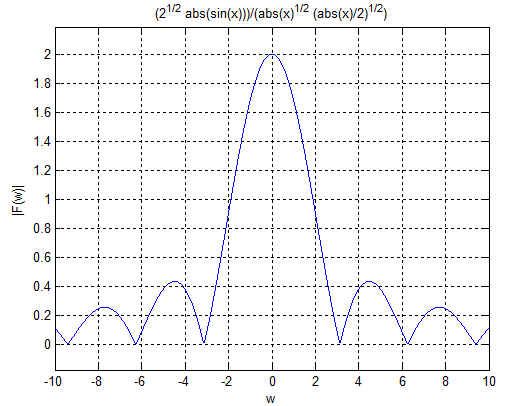
振幅频谱为
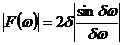
相位频谱为
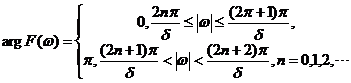
Matlab编程3
Matlab中没有直接傅立叶变换函数,因此需要自己编程实现。(注意:Matlab中自带了离散傅立叶变换的函数)
clear
clc
syms x t d
f=0.5*((x+1)/abs(x+1)-(x-1)/abs(x-1)); %题目中的模拟
F=exp(-i*x*t);%式(33)中第一行最右边一个积分中的积分函数
Fw=int(F,t,-1,1); %积分,这里设定积分区间为[-1,1]
figure(1)
ezplot(f) % 画原函数图
axis([-5 5 0, 2]);
ylabel('f(t)');
xlabel('t');
set(gcf,'color','w');
% figure(2)
ezplot(abs(Fw),-10,10) %画幅度频谱图
ylabel('|F(w)|');
xlabel('w');
grid on
set(gcf,'color','w');
运行结果:
图5 原函数图
图6 幅度频谱图
结果分析:对比图6和图4,可以发现图4是离散的,图6是连续的,傅立叶级数和傅立叶变换频谱的最大区别,其它的都一样。
上面讨论了连续的傅立叶变换,接下来就到了离散的傅立叶变换了!
在图像处理中,很少使用时间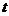
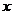
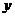
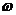
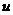
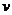
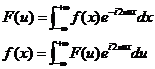
根据式(38),可以将连续的傅立叶变换转化为离散的傅立叶变换(DFT):
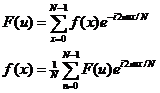
或者
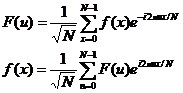
或者
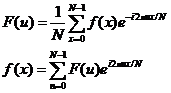
说明:
(1)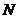
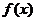
(2)关于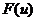
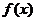
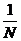
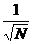
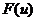
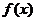
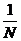
同理,对于根据式(34)可得二维的离散傅立叶变换和反变换为:
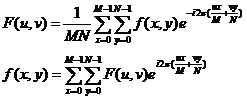
或者
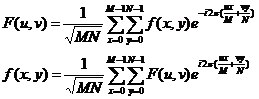
或者
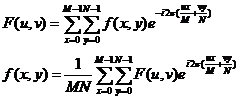
说明:
(1)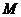
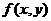
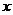
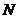
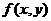
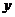
(2)关于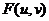
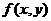
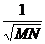
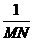
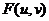
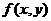
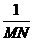
在《MATLAB数字图像处理》一书中,还给出了另外一种形式:
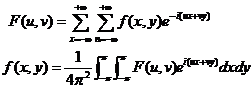
二维离散傅立叶变换物理意义:
式(42)、式(43)、式(44)以及式(45)中的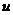
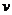
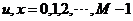
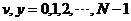
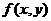
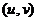
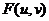
Matlab编程4
对于离散傅立叶变换,Matlab已经自带了函数fft、fft2。这里为了加深对离散傅立叶变换的理解,依据式(44)编写离散傅立叶变换程序如下。
clear
clc
I=imread('pic.jpg'); %二维离散傅立叶变换通常使用在图像分析中,因此这里使用图像来作为实例
imshow(I);
I=rgb2gray(I); %在进行二维离散傅立叶变换前,必须先进行灰度化
I=double(I);
[M,N]=size(I);
for u=1:M %以下就是根据式(44)进行编程。为什么是式(44)而不是式(42)呢?因为经过对比发现,式(44)的计算结果和fft2一致!
for v=1:N
temp=0; %一个临时变量,用于累加
for x=1:M
for y=1:N
temp=temp+I(x,y)*exp(-i*2*pi*((u-1)*(x-1)/M+(v-1)*(y-1)/N));
end
end
myfft(u,v)=temp;
end
end
结果分析:
经过测试,发现上述程序的结果和使用fft2函数得到的结果是一样的。但是,上面程序运行速度非常的慢,运行了30多分钟,还没有计算完毕!而使用fft2,计算过程是瞬间的事情。fft,就是快速傅立叶变换。
参考资料
《高等数学》_广东科技出版社
《复变函数与积分变换》_第三版_华中科技大学数学系_高等教育出版社
《数字图像处理与分析》_北京航空航天大学出版社
《电路》_第5版_高等教育出版社
《概率论》_第二版_中国农业出版社
《MATLAB数字图像处理》_第2版_机械工业出版社






















 9942
9942











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










