棋盘覆盖问题

题目描述：

          

   在一个2k´2k个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为特殊（残缺）方格，且称该棋盘为一特殊棋盘。

  根据特殊方格出现的位置，有种 4k不同的特殊棋盘。

  棋盘覆盖问题：用 4 种不同形态的 L 型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个 L 型骨牌不得重叠覆盖。

  

  

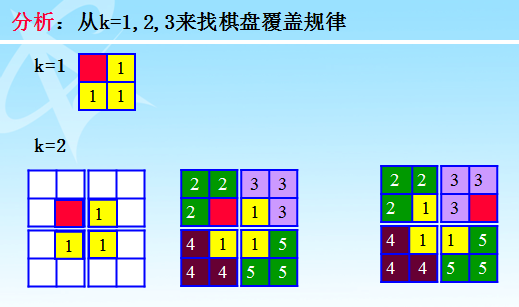
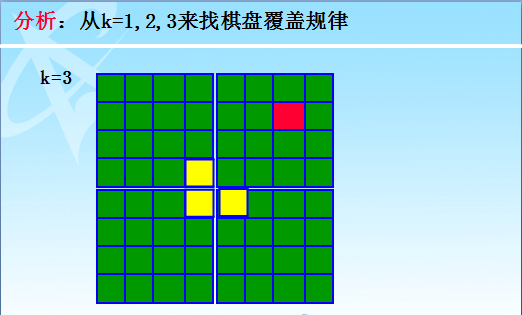
分治法：2k´2k棋盘覆盖问题--4个 2k-1´2k-1棋盘覆盖问题

将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘。特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为棋盘1×1。

int  tr;	// 棋盘左上角方格所在行号 
int  tc;	// 棋盘左上角方格所在列号 
int  dr;	//残缺方格所在行号 
int  dc;	//残缺方格所在列号 		
int  size;	// 棋盘行数列数 
int  s;		//子棋盘行列数 
int  t;		// 用于覆盖子棋盘交界处的格板编号 
全局变量：
int  tile；	//用于覆盖的 L 型三格板的编号 
int  B[n][n]；// 棋盘每个方格所覆盖的 L 型三格板的编号  
void tileboard(int tr, int tc, int dr, int dc, int size)
  {
     int t, s;
     if (size==1) return;
     tile = tile + 1;	t = tile;	
     s = size / 2;
     if ( (dr<tr+s)  &&  (dc<tc+s) )	   /* 处理左上象限 */
          tileboard(tr, tc,  dr, dc, s);	   /*残缺方格位于本象限,覆盖*/
     else {
        B[tr+s-1][tc+s-1] = t;       /*右下角方格置三格板t */
        tileboard(tr,  tc, tr+s-1, tc+s-1,  s);  /* 覆盖其余方格 */
    }
     if ((dr<tr+s) && (dc>=tc+s))	 /* 处理右上象限 */
        tileboard(tr,tc+s,dr,dc,s)  /*残缺方格位于本象限,覆盖*/
    else {
         B[tr+s-1][tc+s] = t;	/* 否则,左下角方格置三格板t */
         tileboard(tr,tc+s,tr+s-1,tc+s,s);        /* 覆盖其余方格 */
    }
    if ((dr>=tr+s) && (dc<tc+s))	       /* 处理左下象限 */
        tileboard(tr+s,tc,dr,dc,s);/*残缺方格位于本象限,覆盖*/
    else {
        B[tr+s][tc+s-1] = t;	/* 否则,右上角方格置三格板t */
        tileboard(tr+s,tc,tr+s,tc+s-1,s);     /* 覆盖其余方格 */
    }
  if ((dr>=tr+s) && (dc>=tc+s))	/* 处理右下象限 */
     tileboard(tr+s,tc+s,dr,dc,s); /*残缺方格位于本象限覆盖*/
  else {
         B[tr+s][tc+s] = t;		/* 否则,左上角方格置三格板t */
        tileboard(tr+s,tc+s,tr+s,tc+s,s);   /* 覆盖其余方格 */
    }
 }