动态规划基本概念
动态规划算法是经过拆分问题，定义问题的状态与状态之间的关系，使得问题可以以递推（或者说分治）的方式去解决。在学习动态规划以前须要明确掌握几个重要概念。java
阶段：对于一个完整的问题过程，适当的切分为若干个相互联系的子问题，每次在求解一个子问题，则对应一个阶段，整个问题的求解转化为按照阶段次序去求解。算法
状态：状态表示每一个阶段开始时所处的客观条件，即在求解子问题时的已知条件。状态描述了研究的问题过程当中的情况。数组
决策：决策表示当求解过程处于某一阶段的某一状态时，能够根据当前条件做出不一样的选择，从而肯定下一个阶段的状态，这种选择称为决策。性能
策略：由全部阶段的决策组成的决策序列称为全过程策略，简称策略。学习
最优策略：在全部的策略中，找到代价最小，性能最优的策略，此策略称为最优策略。优化
状态转移方程：状态转移方程是肯定两个相邻阶段状态的演变过程，描述了状态之间是如何演变的。
使用场景
能采用动态规划求解的问题通常要具备 如下3 个性质：
（1）最优化：若是问题的最优解所包含的子问题的解也是最优的，就称该问题具备最优子结构，即知足最优化原理。子问题的局部最优将致使整个问题的全局最优。换句话说，就是问题的一个最优解中必定包含子问题的一个最优解。it
（2）无后效性：即某阶段状态一旦肯定，就不受这个状态之后决策的影响。也就是说，某状态之后的过程不会影响之前的状态，只与当前状态有关，与其余阶段的状态无关，特别是与未发生的阶段的状态无关。io
（3）重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被屡次使用到。（该性质并非动态规划适用的必要条件，可是若是没有这条性质，动态规划算法同其余算法相比就不具有优点）
算法流程
（1）首先确认dp数组以及下标的含义：将问题的不一样阶段时期的不一样状态描述出来。确认dp数组以及下标的含义. 比如机器人走方格，我们定义dp[i][j],代表着i为多少行,j为多少列，dp[i][j]代表最后一共有多少到达终点的路径。再比如 最长回文子序列中，dp[i][j]代表了回文子序列的长度
（2）肯定决策并写出状态转移方程：根据相邻两个阶段的各个状态之间的关系肯定决策。要注意是否区分情况
（3）寻找初始化边界：通常而言，状态转移方程是递推式，必须有一个递推的边界条件。dp[i][j]是否要初始化true或者false，是否初始化为0
（4）for循环的遍历顺序。变量是从前往后遍历还是从后往前遍历，是从上到下遍历，还是从下到上遍历。这个判断的标准主要是dp[i][j]是依据谁来推导出来的。
实战练习
股票问题
只能买卖一次
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
若是你最多只容许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 由于卖出价格须要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种状况下, 没有交易完成, 因此最大利润为 0。这道题我们使用常规的解题思路来解决，因为我感觉使用动态规划步骤有点绕，但是这是一道动态规划的题目。
状态的含义
有 买入（buy） 和 卖出（sell） 这两种状态。
状态转移方程
对于买来讲，买以后能够卖出（进入卖状态），也能够再也不进行股票交易（保持买状态）。
对于卖来讲，卖出股票后不在进行股票交易（还在卖状态）。
只有在手上的钱才算钱，手上的钱购买当天的股票后至关于亏损。也就是说当天买的话意味着损失-prices[i]，当天卖的话意味着增长prices[i]，当天卖出总的收益就是 buy+prices[i] 。
因此咱们只要考虑当天买和以前买哪一个收益更高，当天卖和以前卖哪一个收益更高。
buy = max(buy, -price[i]) （注意：根据定义 buy 是负数）
sell = max(sell, prices[i] + buy)初始值
第一天 buy = -prices[0], sell = 0，最后返回 sell 便可。
function maxProfit(prices) {
if(prices.length <= 1)
return 0;
var buy = -prices[0];
var sell = 0;
for(var i = 1; i < prices.length; i++) {
buy = Math.max(buy, -prices[i]);
sell = Math.max(sell, prices[i] + buy);
}
return sell;
}可以买卖多次
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你能够尽量地完成更多的交易（屡次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉以前的股票）。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能得到利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能得到利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易>所能得到利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，以后再将它们卖出。
由于这样属于同时参与了多笔交易，你必须在再次购买前出售掉以前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种状况下, 没有交易完成, 因此最大利润为 0。dp状态
有 买入（buy） 和 卖出（sell） 这两种状态。
状态转移方程
对比上题，这里能够有无限次的买入和卖出，也就是说 买入 状态以前可拥有 卖出 状态，因此买入的转移方程须要变化。
buy = max(buy, sell - price[i])
sell = max(sell, buy + prices[i] )初始值
第一天 buy = -prices[0], sell = 0，最后返回 sell 便可。
function maxProfit(prices) {
if(prices.length <= 1)
return 0;
int buy = -prices[0], sell = 0;
for(int i = 1; i < prices.length; i++) {
sell = Math.max(sell, prices[i] + buy);
buy = Math.max( buy,sell - prices[i]);
}
return sell;
}最多买卖2次
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多能够完成 两笔 交易。
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉以前的股票）。
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能得到利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能得到利润 = 4-1 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能得到利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，以后再将它们卖出。
由于这样属于同时参与了多笔交易，你必须在再次购买前出售掉以前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这个状况下, 没有交易完成, 因此最大利润为 0。dp状态
有 第一次买入（fstBuy） 、 第一次卖出（fstSell）、第二次买入（secBuy） 和 第二次卖出（secSell） 这四种状态。
状态转移方程
这里能够有两次的买入和卖出，也就是说 买入 状态以前可拥有 卖出 状态，因此买入和卖出的转移方程须要变化。
fstBuy = max(fstBuy ， -price[i])
fstSell = max(fstSell，fstBuy + prices[i] )
secBuy = max(secBuy ，fstSell -price[i]) (受第一次卖出状态的影响)
secSell = max(secSell ，secBuy + prices[i] )初始值
一开始 fstBuy = -prices[0]
买入后直接卖出，fstSell = 0
买入后再卖出再买入，secBuy - prices[0]
买入后再卖出再买入再卖出，secSell = 0
最后返回 secSell 。
function maxProfit(prices) {
let fstBuy = -prices[0], secBuy = -prices[0];
let fstSell = 0, secSell = 0;
for(var i = 0; i < prices.length; i++) {
fstBuy = Math.max(fstBuy, -prices[i]);
fstSell = Math.max(fstSell, fstBuy + prices[i]);
secBuy = Math.max(secBuy, fstSell - prices[i]);
secSell = Math.max(secSell, secBuy + prices[i]);
}
return secSell;
}回文问题
首先要区分 子串和子序列的区别，回文子串是要连续的，回文子序列可不是连续的！回文子序列都是动态规划经典题目。
回文子串
给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。
示例 1：
输入："abc" 输出：3 解释：三个回文子串: "a", "b", "c"
示例 2：
输入："aaa" 输出：6 解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示：
输入的字符串长度不会超过 1000 。首先需要明确的一点是要求回文，即需要两个指针分别指向头和尾，所以需要i,j。我们按照上面步骤解释
确认dp[i][j]的含义
代表我们要求的结果即 字符串中有多少回文子串
确认递推公式，
主要看dp[i][j]是由什么得到的,这里我们需要判断str[i]是否等于str[j], 当单字符串a,以及aa字符串这是一种情况我们dp[i][j]我们设置为true.当我们的i和j相差大于1的时候，比如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
确定dp初始化
dp[i][j]初始化为false
确定遍历顺序
我们在分析递推公式的时候看到，我们的dp[i][j]是依据dp[i+1][j-1]得到，如果我们将i，j看做行列，那么可以想象dp[i+1][j-1]在dp[i][j]的左下角。为了保证我们dp[i][j]是由dp[i+1][j-1]推导出来的，所以我们从下到上，从左到右遍历。所以我们得到
const countSubstrings = (s) => {
const strLen = s.length;
let numOfPalindromicStr = 0;
let dp = Array.from(Array(strLen), () => Array(strLen).fill(false));
for(let j = 0; j < strLen; j++) {
for(let i = 0; i <= j; i++) {
if(s[i] === s[j]) {
if((j - i) < 2) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i+1][j-1];
}
numOfPalindromicStr += dp[i][j] ? 1 : 0;
}
}
}
return numOfPalindromicStr;
}最长回文子序列
给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1: 输入: "bbbab" 输出: 4 一个可能的最长回文子序列为 "bbbb"。
示例 2: 输入:"cbbd" 输出: 2 一个可能的最长回文子序列为 "bb"。
提示：
1 <= s.length <= 1000
s 只包含小写英文字母本题是求非连续的回文序列.首先我们还是先按解题的几步去解题
首先我们确定dp数组的含义
我们用dp[i][j]来表示[i,j]范围内的最长回文子序列的长度dp[i][j]
确定递推公式
相对于上一题的连续，非连续相对简单。我们只要思考dp[i][j]的规律，也就是我们常做的找规律，我们设想，头1和尾1字符串相等，那么我们就要对比头2和尾2，相应回想我们dp[i][j]数组含义代表数量，所以我们的递推公式为dp[i][j] = dp[i+1][j-1]+ 2。这是第一种情况，就是出现重复的情况。我们一直说动态规划要分情况。如果我们没有找到回文，那么我们可以头+1，或者尾+1.所以我们第二个递推公式是 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}确定初始化
首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
确定遍历顺序
从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出，dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j]，也就是从矩阵的角度来说，dp[i][j] 下一行的数据。所以遍历i的时候一定要从下到上遍历，这样才能保证，下一行的数据是经过计算的。我们的i其实代表的是第几行，j代表的是第几列，如果是方格的话，最终的结果就是右上角的值
const longestPalindromeSubseq = (s) => {
const strLen = s.length;
let dp = Array.from(Array(strLen), () => Array(strLen).fill(0));
for(let i = 0; i < strLen; i++) {
dp[i][i] = 1;
}
for(let i = strLen - 1; i >= 0; i--) {
for(let j = i + 1; j < strLen; j++) {
if(s[i] === s[j]) {
dp[i][j] = dp[i+1][j-1] + 2;
} else {
dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
}
}
}
return dp[0][strLen - 1];
};最长上升问题（连续 非连续）
最长上升子序列
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1： 输入：nums = [10,9,2,5,3,7,101,18] 输出：4 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
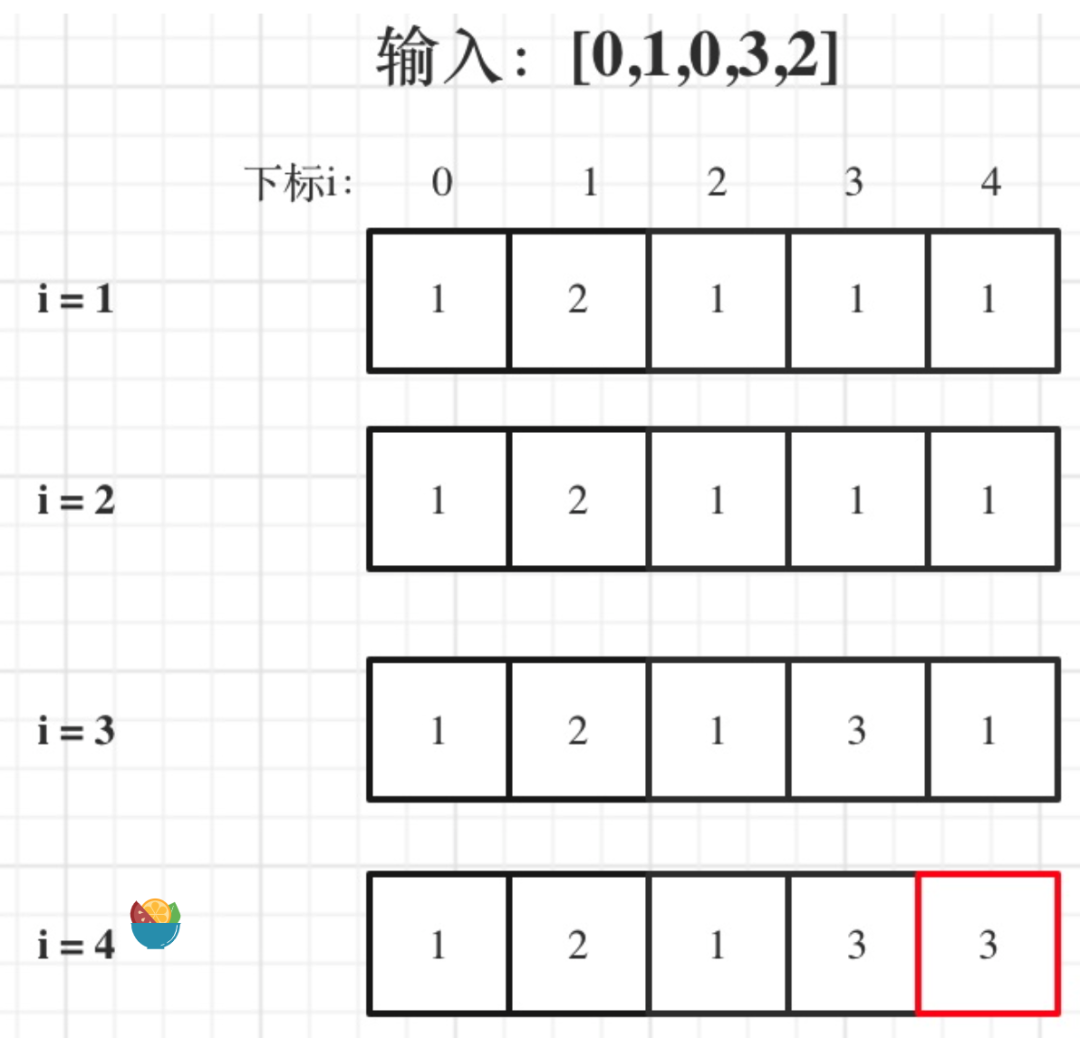
示例 2： 输入：nums = [0,1,0,3,2,3] 输出：4
示例 3： 输入：nums = [7,7,7,7,7,7,7] 输出：1
提示：
1 <= nums.length <= 2500
-10^4 <= nums[i] <= 104dp数组的含义
dp[i]表示i之前包括i的最长上升子序列的长度。
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
确认初始化
dp[i] 最长上升子序列起始大小至少为1
确认遍历顺序
dp[i] 是有0到i-1各个位置的最长升序子序列 推导而来，那么遍历i一定是从前向后遍历。j其实就是0到i-1，遍历i的循环在外层，遍历j则在内层，代码如下：
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
}
if (dp[i] > result) result = dp[i]; // 取长的子序列
}
const lengthOfLIS = (nums) => {
let dp = Array(nums.length).fill(1);
let result = 1;
for(let i = 1; i < nums.length; i++) {
for(let j = 0; j < i; j++) {
if(nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
result = Math.max(result, dp[i]);
}
return result;
};最长连续递增序列
给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1： 输入：nums = [1,3,5,4,7] 输出：3 解释：最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。
示例 2： 输入：nums = [2,2,2,2,2] 输出：1 解释：最长连续递增序列是 [2], 长度为1。
提示：
0 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9
#确认dp数组的含义
dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。
确定递推公式
如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度 一定等于 以i为结尾的数组的连续递增的子序列长度 + 1 。dp[i + 1] = dp[i] + 1;需要比较 num[i+1]以及num[i]。
dp数组如何初始化
以下标i为结尾的数组的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。dp[i]应该初始1;
确认遍历顺序
从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。从前到后 所以i一定是i++
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] > nums[i]) { // 连续记录
dp[i + 1] = dp[i] + 1; // 递推公式
}
}
const findLengthOfLCIS = (nums) => {
let dp = Array(nums.length).fill(1);
for(let i = 0; i < nums.length - 1; i++) {
if(nums[i+1] > nums[i]) {
dp[i+1] = dp[i]+ 1;
}
}
return Math.max(...dp);
};最长重复问题 (连续 非连续)
最长重复子数组
给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。
示例：
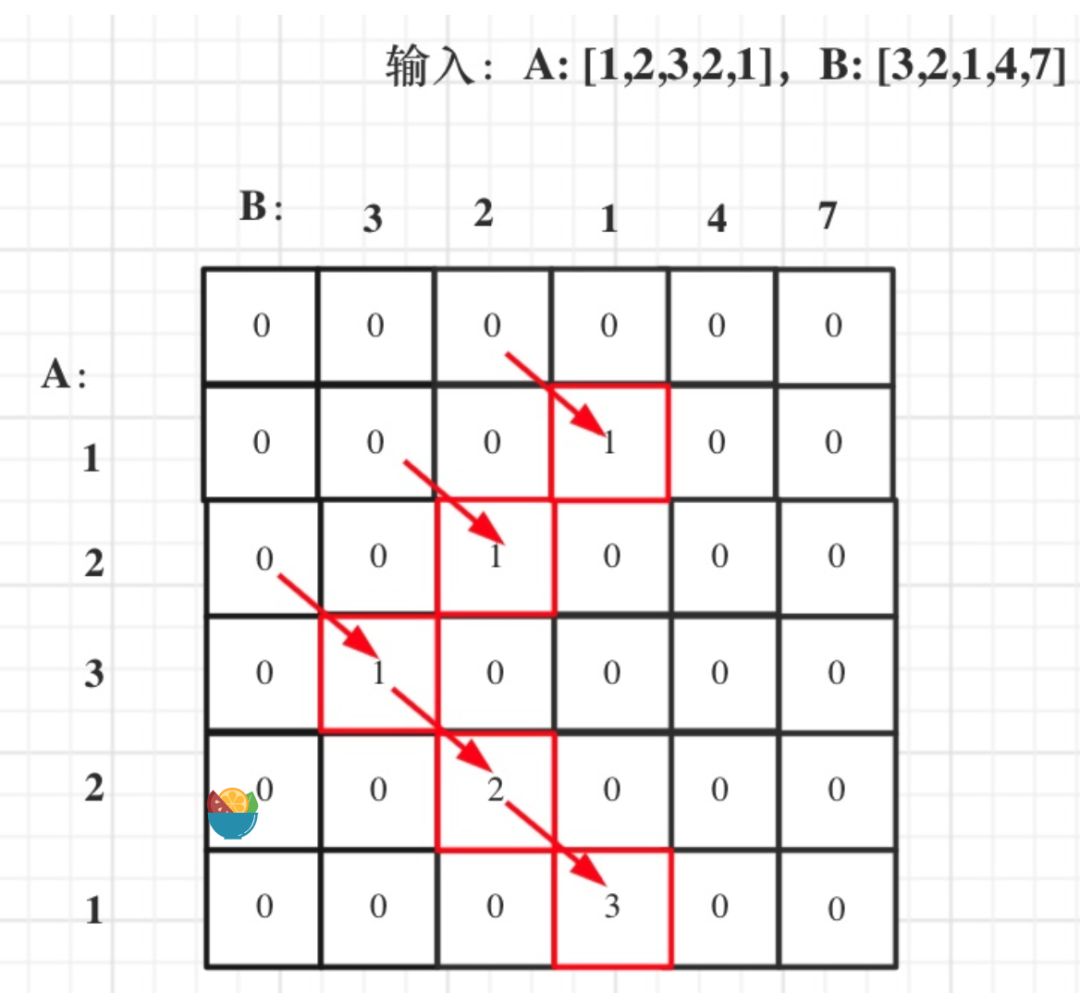
输入：A: [1,2,3,2,1] B: [3,2,1,4,7] 输出：3 解释： 长度最长的公共子数组是 [3, 2, 1] 。
提示：
1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100确定dp数组的含义
dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。
确定递推公式
根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。
即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;
根据递推公式可以看出，遍历i 和 j 要从1开始！
dp数组如何初始化
根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！
但dp[i][0] 和dp[0][j]要初始值，因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
确定遍历顺序
for (int i = 1; i <= A.size(); i++) {
for (int j = 1; j <= B.size(); j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
最长公共子序列
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列，则返回 0。
示例 1:
输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。
示例 2:
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。
示例 3:
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。
提示:
1 <= text1.length <= 1000
1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。确定dp数组（dp table）以及下标的含义
dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
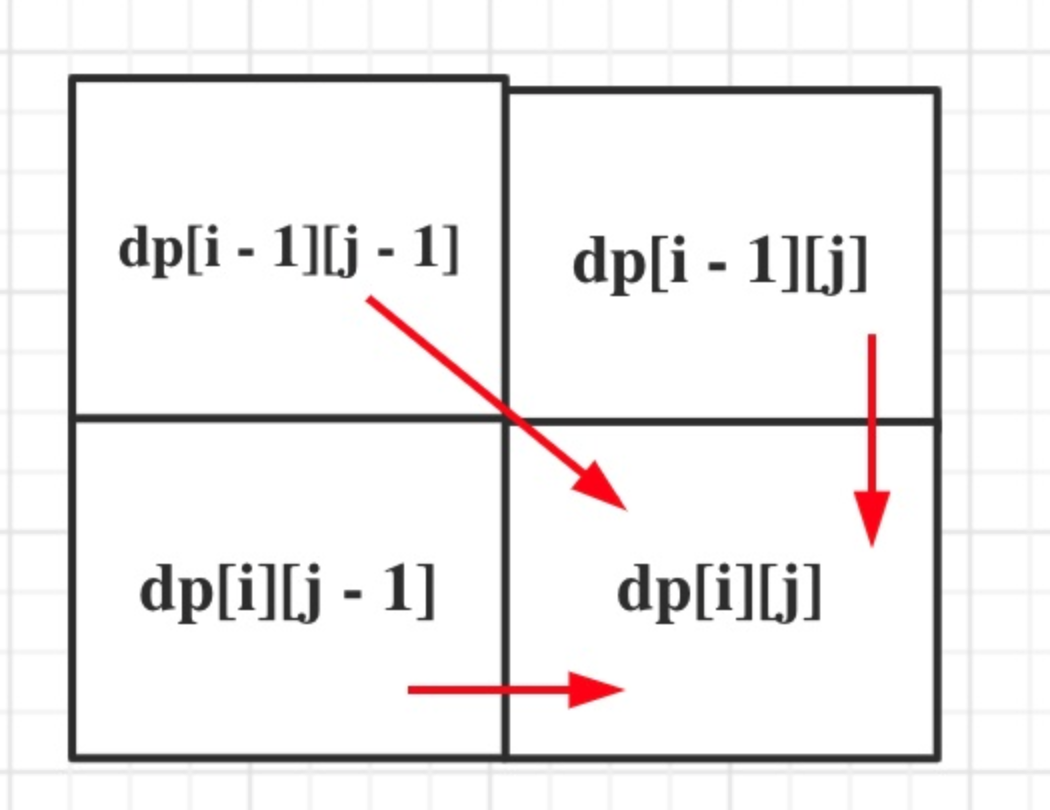
确定递推公式
text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
if (text1[i - 1] == text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}dp数组如何初始化
test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
同理dp[0][j]也是0。
其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。
确定遍历顺序
最大子序列和
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
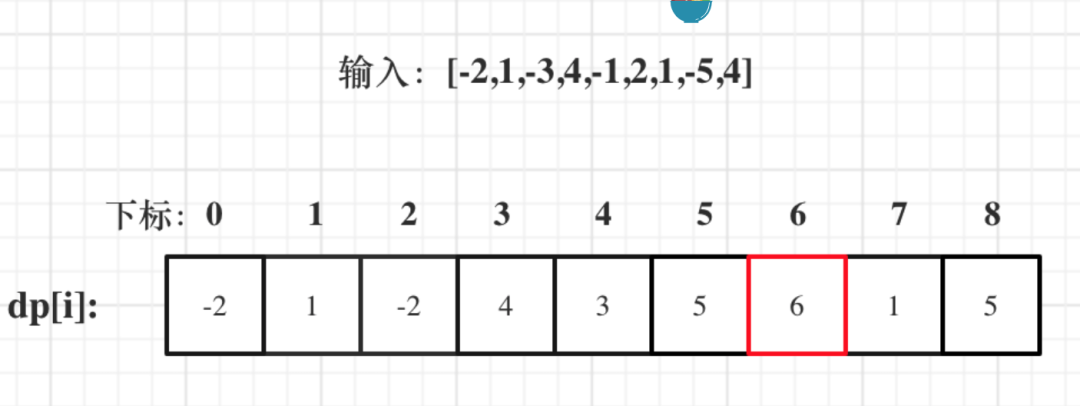
示例: 输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6确定dp数组（dp table）
dp[i]：包括下标i之前的最大连续子序列和为dp[i]。
确定递推公式
dp[i]只有两个方向可以推出来：dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和nums[i]，即：从头开始计算当前连续子序列和.一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。dp[0]应该是多少呢?根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。
确定遍历顺序
递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。
const maxSubArray = nums => {
// 数组长度，dp初始化
const len = nums.length;
let dp = new Array(len).fill(0);
// 最大值初始化为dp[0]
let max = dp[0];
for (let i = 1; i < len; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
// 更新最大值
max = Math.max(max, dp[i]);
}
return max;
};判断A是否是B子序列以及子序列个数
判断 子序列
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
示例 1： 输入：s = "abc", t = "ahbgdc" 输出：true
示例 2： 输入：s = "axc", t = "ahbgdc" 输出：false
提示：
0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。编辑距离的入门题目
确定dp数组（dp table）
dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。判断s是否为t的子序列。即t的长度是大于等于s的。
确定递推公式
if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1（如果不理解，在回看一下dp[i][j]的定义）if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];
dp数组如何初始化
dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。因为这样的定义在dp二维矩阵中可以留出初始化的区间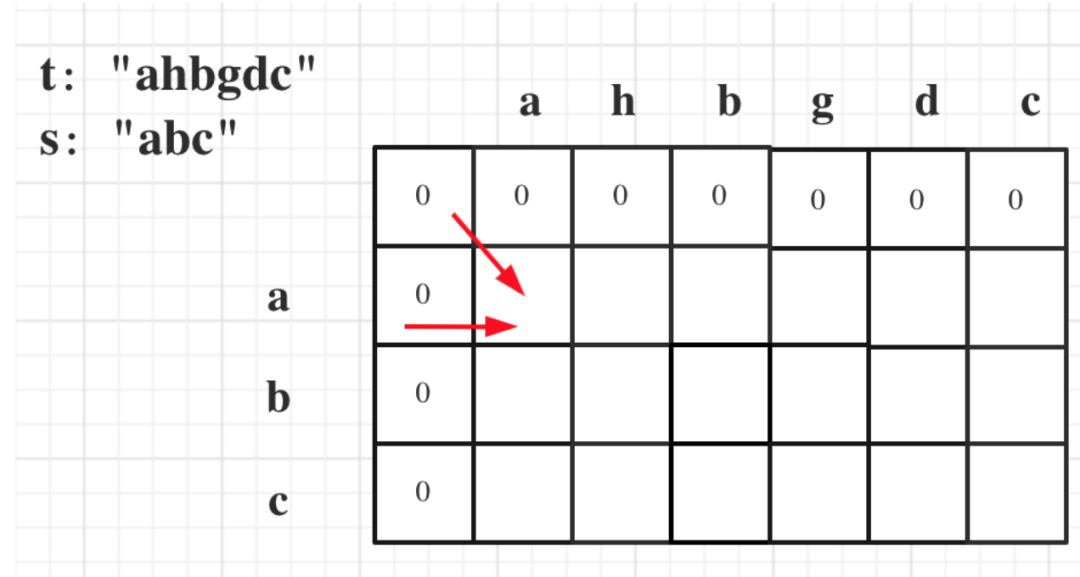
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。其实这里只初始化dp[i][0]就够了，但一起初始化也方便，所以就一起操作了
确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右
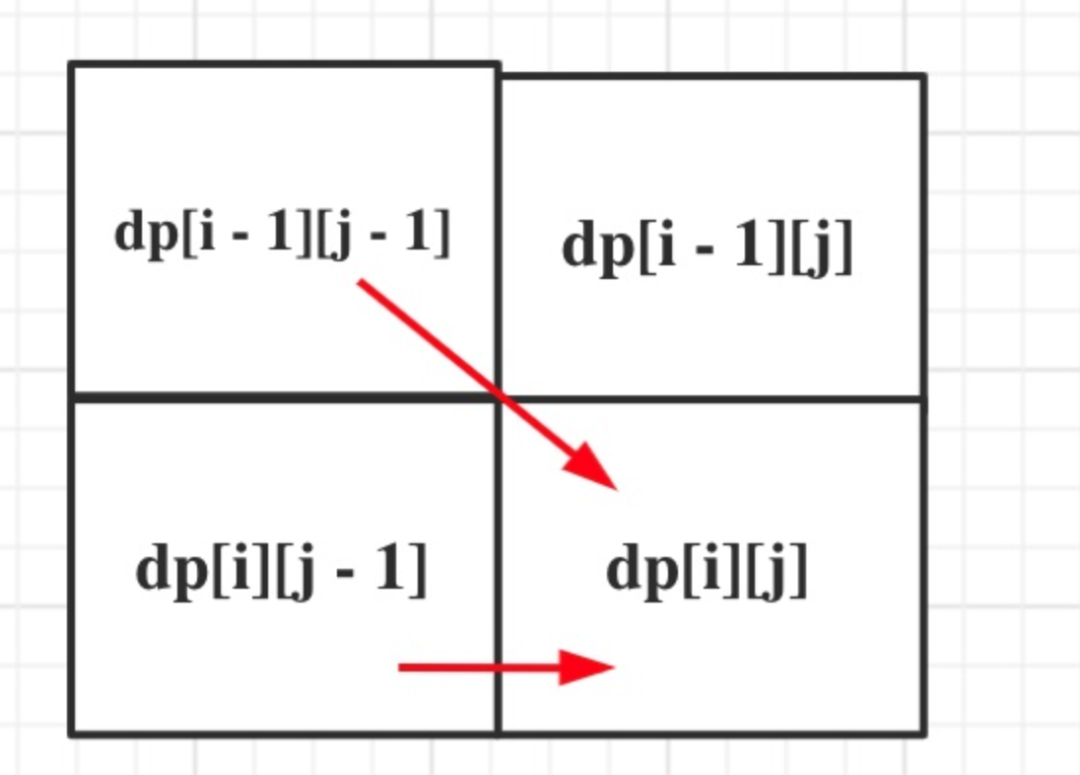
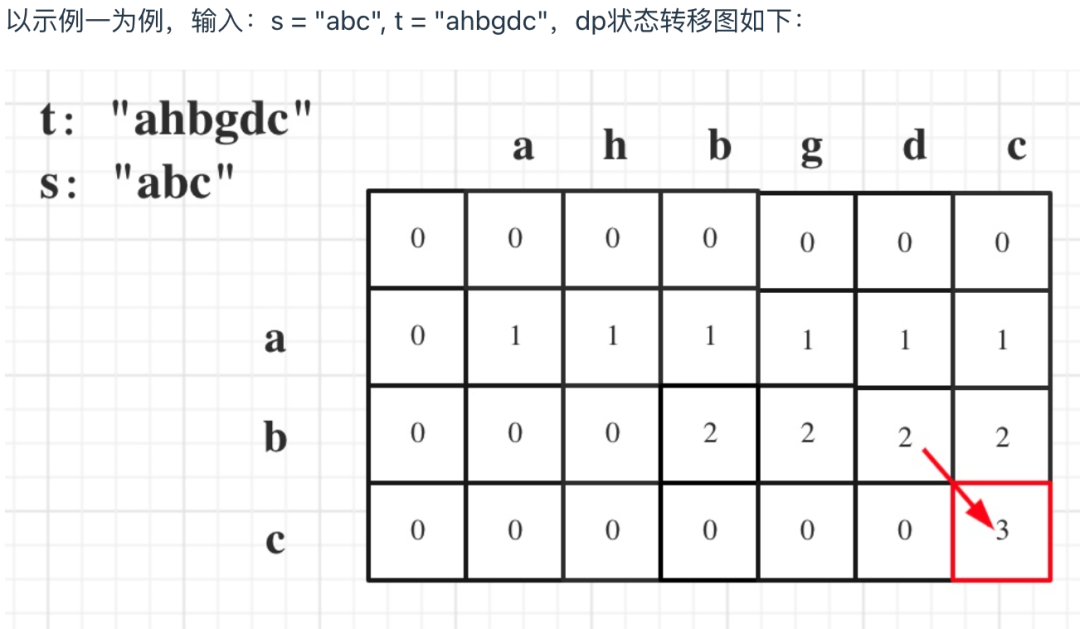dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3， 而s.size() 也为3。所以s是t 的子序列，返回true。
const isSubsequence = (s, t) => {
// s、t的长度
const [m, n] = [s.length, t.length];
// dp全初始化为0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 更新dp[i][j]，两种情况
if (s[i - 1] === t[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
// 遍历结束，判断dp右下角的数是否等于s的长度
return dp[m][n] === m ? true : false;
};背包问题
01背包问题- 分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200
示例 1: 输入: [1, 5, 11, 5] 输出: true 解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2: 输入: [1, 2, 3, 5] 输出: false 解释: 数组不能分割成两个元素和相等的子集.
提示：
1 <= nums.length <= 200
1 <= nums[i] <= 100背包问题，大家都知道，有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。要注意题目描述中商品是不是可以重复放入。即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法还是不一样的。要明确本题中我们要使用的是01背包，因为元素我们只能用一次。
回归主题：首先，本题要求集合里能否出现总和为 sum / 2 的子集。那么来一一对应一下本题，看看背包问题如果来解决。只有确定了如下四点，才能把01背包问题套到本题上来。
背包的体积为sum / 2
背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
背包如果正好装满，说明找到了总和为 sum / 2 的子集。
背包中每一个元素是不可重复放入。
确定dp数组以及下标的含义
01背包中，dp[j] 表示：容量为j的背包，所背的物品价值可以最大为dp[j]。套到本题，dp[j]表示 背包总容量是j，最大可以凑成j的子集总和为dp[j]。
确定递推公式
01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
dp数组如何初始化
从dp[j]的定义来看，首先dp[0]一定是0。
确定遍历顺序
如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}01背包相对于本题，主要要理解，题目中物品是nums[i]，重量是nums[i]，价值也是nums[i]，背包体积是sum/2。
var canPartition = function(nums) {
const sum = (nums.reduce((p, v) => p + v));
if (sum & 1) return false;
const dp = Array(sum / 2 + 1).fill(0);
for(let i = 0; i < nums.length; i++) {
for(let j = sum / 2; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
if (dp[j] === sum / 2) {
return true;
}
}
}
return dp[sum / 2] === sum / 2;
};完全背包问题
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5] 输出: 4 解释: 有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1
示例 2: 输入: amount = 3, coins = [2] 输出: 0 解释: 只用面额2的硬币不能凑成总金额3。
示例 3: 输入: amount = 10, coins = [10] 输出: 1
注意，你可以假设：
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数本题和纯完全背包不一样，纯完全背包是能否凑成总金额，而本题是要求凑成总金额的个数！注意题目描述中是凑成总金额的硬币组合数，为什么强调是组合数呢？
例如示例一：
5 = 2 + 2 + 1
5 = 2 + 1 + 2这是一种组合，都是 2 2 1。如果问的是排列数，那么上面就是两种排列了。组合不强调元素之间的顺序，排列强调元素之间的顺序
确定dp数组以及下标的含义
dp[j]：凑成总金额j的货币组合数为dp[j]
确定递推公式
dp[j] （考虑coins[i]的组合总和） 就是所有的dp[j - coins[i]]（不考虑coins[i]）相加。所以递推公式：dp[j] += dp[j - coins[i]];求装满背包有几种方法，一般公式都是：dp[j] += dp[j - nums[i]];
dp数组如何初始化
首先dp[0]一定要为1，dp[0] = 1是 递归公式的基础。从dp[i]的含义上来讲就是，凑成总金额0的货币组合数为1。下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
确定遍历顺序
因为纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！而本题要求凑成总和的组合数，元素之间要求没有顺序。所以纯完全背包是能凑成总和就行，不用管怎么凑的。本题是求凑出来的方案个数，且每个方案个数是为组合数。那么本题，两个for循环的先后顺序可就有说法了。我们先来看 外层for循环遍历物品（钱币），内层for遍历背包（金钱总额）的情况。
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}假设：coins[0] = 1，coins[1] = 5。那么就是先把1加入计算，然后再把5加入计算，得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。所以这种遍历顺序中dp[j]里计算的是组合数！如果把两个for交换顺序，代码如下：
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}背包容量的每一个值，都是经过 1 和 5 的计算，包含了{1, 5} 和 {5, 1}两种情况。此时dp[j]里算出来的就是排列数！
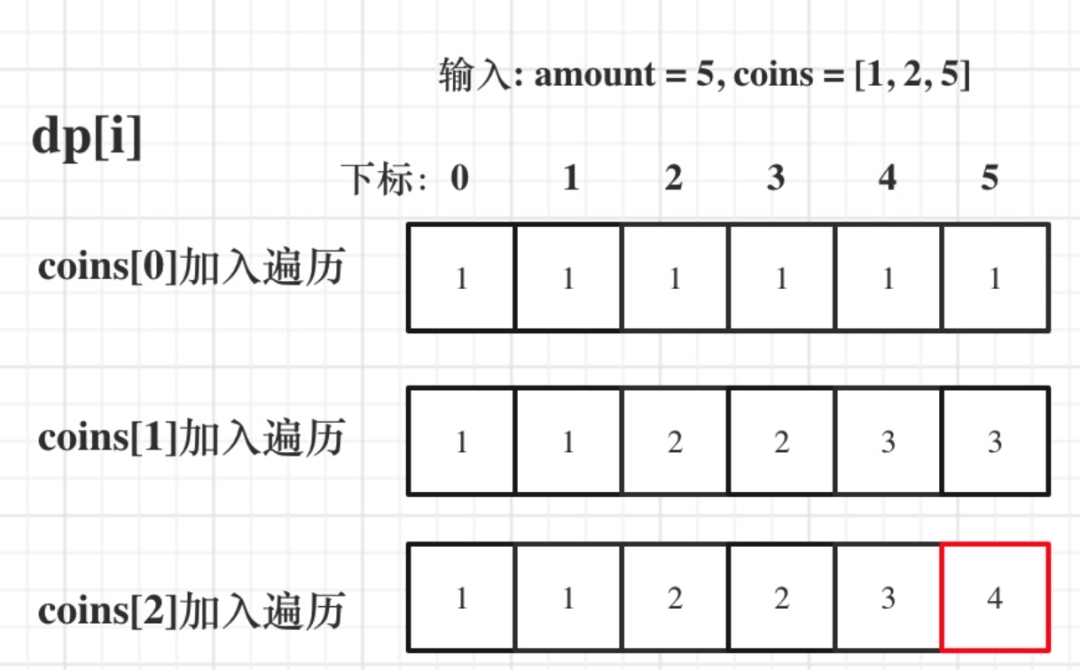
const change = (amount, coins) => {
let dp = Array(amount + 1).fill(0);
dp[0] = 1;
for(let i =0; i < coins.length; i++) {
for(let j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}不同路径问题
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？
输入：m = 3, n = 7
输出：28
示例 2：
输入：m = 2, n = 3
输出：3
解释： 从左上角开始，总共有 3 条路径可以到达右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
示例 3：
输入：m = 7, n = 3
输出：28
示例 4：
输入：m = 3, n = 3
输出：6
提示：
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
确定dp数组（dp table）以及下标的含义
dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
确定递推公式
想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。
dp数组的初始化
如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。
for (let i = 0; i < m; i++) dp[i][0] = 1;
for (let j = 0; j < n; j++) dp[0][j] = 1;确定遍历顺序
这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
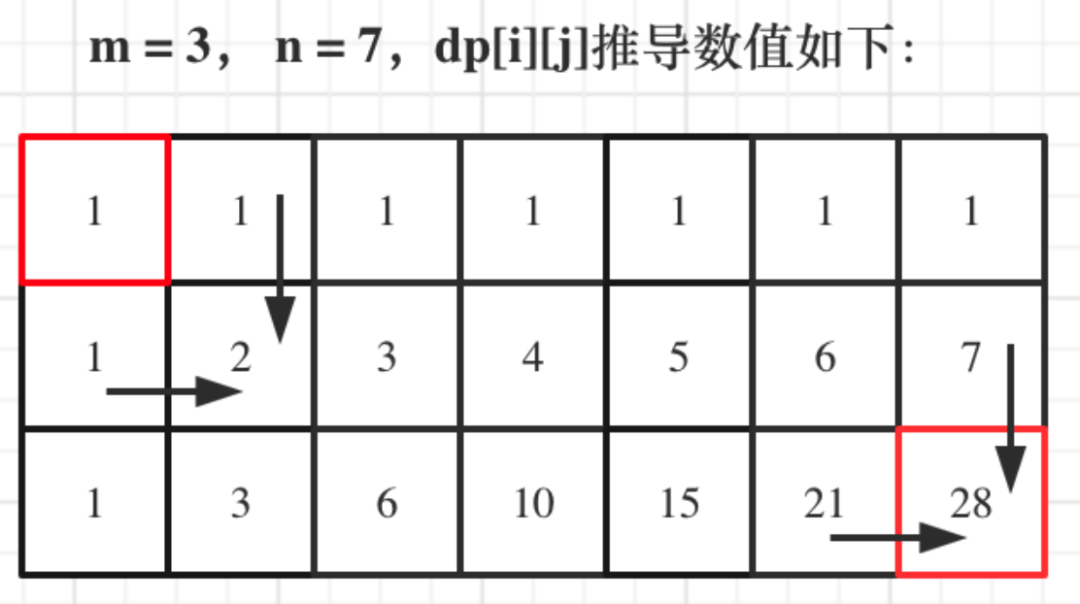
var uniquePaths = function(m, n) {
const dp = Array(m).fill().map(item => Array(n))
for (let i = 0; i < m; ++i) {
dp[i][0] = 1
}
for (let i = 0; i < n; ++i) {
dp[0][i] = 1
}
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
};爬楼梯问题
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。
示例 1：
输入：2
输出：2
解释： 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2：
输入：3
输出：3
解释： 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶确定dp数组以及下标的含义
dp[i]：爬到第i层楼梯，有dp[i]种方法
确定递推公式
如果可以推出dp[i]呢？从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！所以dp[i] = dp[i - 1] + dp[i - 2] 。在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性！
dp数组如何初始化
在回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]中方法。那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但都基本是直接奔着答案去解释的。例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶。但总有点牵强的成分。那还这么理解呢：我就认为跑到第0层，方法就是0啊，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0.其实这么争论下去没有意义，大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1。从dp数组定义的角度上来说，dp[0] = 0 也能说得通。需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。所以本题其实就不应该讨论dp[0]的初始化！我相信dp[1] = 1，dp[2] = 2，这个初始化大家应该都没有争议的。所以我的原则是：不考虑dp[0]如果初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。
确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的
var climbStairs = function(n) {
// dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
// dp[i] = dp[i - 1] + dp[i - 2]
let dp = [1 , 2]
for(let i = 2; i < n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n - 1]
};最后, 送人玫瑰，手留余香，觉得有收获的朋友可以点赞，关注一波 ，我们组建了高级前端交流群，如果您热爱技术，想一起讨论技术，交流进步，不管是面试题，工作中的问题，难点热点都可以在交流群交流，为了拿到大Offer，邀请您进群，入群就送前端精选100本电子书以及下方前端精选资料 添加 下方小助手二维码就可以进群。让我们一起学习进步.
推荐阅读
（点击标题可跳转阅读）
[面试必问]-你不知道的 React Hooks 那些糟心事
[面试必问]-全网最全 React16.0-16.8 特性总结
[架构分享]- 微前端qiankun+docker+nginx自动化部署
[架构分享]-石墨文档 Websocket 百万长连接技术实践
觉得本文对你有帮助？请分享给更多人
关注「React中文社区」加星标，每天进步
点个赞👍🏻，顺便点个 在看 支持下我吧
981
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
