目录
1. 均方误差(Mean Squared Error, MSE)
2. 平均绝对误差(Mean Absolute Error, MAE)
1. 交叉熵损失(Cross-Entropy Loss, CEL)
(1)二分类交叉熵(Binary Cross-Entropy, BCE)
(2)多分类交叉熵(Categorical Cross-Entropy, CCE)
1. Wasserstein距离(Wasserstein Distance)
引言
损失函数(Loss Function),又称代价函数(Cost Function)或目标函数(Objective Function,注:目标函数有时泛指最大化/最小化目标,损失函数是其用于“最小化误差”的子类),是机器学习与深度学习中衡量模型预测结果与真实标签(Ground Truth)之间差异程度的核心数学工具。其值越小,代表模型的预测越接近真实情况;模型训练的本质,就是通过优化算法(如梯度下降)不断最小化损失函数的过程。
一、损失函数的核心作用
损失函数是连接“模型预测”与“优化目标”的桥梁,其核心作用可归纳为三点:
-
量化误差:将“预测准不准”这一主观判断,转化为可计算的数值(如预测房价与真实房价的差值、预测“猫”却输出“狗”的概率偏差)。
-
指导优化:为模型参数更新提供方向——通过计算损失函数对参数的梯度(Gradient),确定参数应“增大”还是“减小”以降低损失。
-
定义目标:不同的损失函数对应不同的优化目标(如“最小化绝对误差”“最大化分类正确率对应的概率”),直接决定模型的学习偏好。
二、损失函数的分类框架
根据机器学习任务的核心目标(预测连续值/离散类别/概率分布),损失函数可分为三大类:回归任务损失函数、分类任务损失函数、分布匹配损失函数。各类别下又包含多个常用函数,适用场景与数学特性差异显著。
下面的概括偏数学,读者可以结合我的另一篇博客中第六点损失函数与对应ppt更加通俗易懂地理解损失函数和损失函数的应用,附文:
(一)回归任务损失函数
回归任务的目标是预测连续型数值(如房价、温度、销售额),损失函数主要衡量“预测值与真实值的数值偏差”。
1. 均方误差(Mean Squared Error, MSE)
别名:L2损失(因基于L2范数)、平方损失。
数学公式:
单个样本:
批量样本:
其中,y是真实标签,y^是模型预测值,N是样本数量。
核心特性:
-
对异常值敏感:误差被平方放大,异常值(如真实房价100万,模型预测1000万)会产生极大损失,主导参数更新方向。
-
可导性好:函数连续且一阶、二阶导数均存在,便于使用梯度下降、牛顿法等优化算法。
适用场景:
数据中无明显异常值的回归任务(如普通商品价格预测、身高体重预测);深度学习中线性回归、神经网络回归输出层的默认损失(如预测图片中物体的坐标)。
2. 平均绝对误差(Mean Absolute Error, MAE)
别名:L1损失(因基于L1范数)、绝对损失。
数学公式:
单个样本:
批量样本:
核心特性:
-
对异常值鲁棒:误差未被平方,异常值的影响被限制,更关注多数样本的拟合效果。
-
不可导点:在y^=y处(误差为0)导数不存在(左导数=-1,右导数=1),可能影响优化效率(需用次梯度等方法处理)。
适用场景:
数据中存在较多异常值的回归任务(如极端天气下的用电量预测、包含错误记录的销售额数据)。
3. MSE与MAE的对比
| 对比维度 | 均方误差(MSE) | 平均绝对误差(MAE) |
|---|---|---|
| 异常值敏感性 | 高(平方放大误差) | 低(绝对误差无放大) |
| 可导性 | 全区间可导,优化平滑 | 在误差=0处不可导,需次梯度 |
| 最优解特性 | 偏向“最小化平方和”,易受极端值影响 | 偏向“中位数”,更稳健 |
| 适用数据 | 无异常值、正态分布误差的数据 | 有异常值、误差分布不对称的数据 |
4. 其他回归损失函数
-
Huber损失:结合MSE和MAE的优点,误差小时用MSE(平滑优化),误差大时用MAE(抗异常值),公式为:
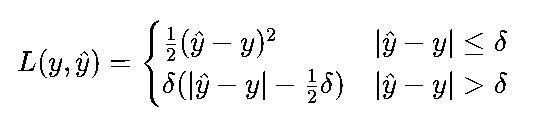
其中δ为阈值(通常取1.0),适用于需要平衡“平滑优化”与“抗异常值”的场景(如自动驾驶中的距离预测)。
-
Log-Cosh损失:用双曲余弦函数的对数近似MSE,具有MSE的平滑性,同时对异常值的敏感度低于MSE,公式为:
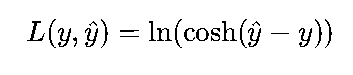
适用于深度学习中对异常值有一定容忍度的回归任务。
(二)分类任务损失函数
分类任务的目标是预测离散类别标签(如“猫/狗”二分类、“苹果/香蕉/橙子”多分类),损失函数主要衡量“预测类别概率分布与真实类别分布的差异”。
1. 交叉熵损失(Cross-Entropy Loss, CEL)
交叉熵源于信息论,衡量两个概率分布(真实分布p与预测分布q)的“不相似程度”,是分类任务中最核心的损失函数。
(1)二分类交叉熵(Binary Cross-Entropy, BCE)
适用场景:任务输出仅两个类别(如“正/负”“患病/健康”),模型输出层通常用Sigmoid函数(或其他非线性映射函数)将预测值映射到[0,1]区间(代表“属于正类的概率”)。
数学公式:
单个样本:
批量样本:
其中,y∈{0,1}(真实标签,0为负类,1为正类),p^是模型预测的“正类概率”,1−p^是“负类概率”。
核心逻辑:
-
若真实标签y=1(正类),损失简化为−ln(p^):p^越接近1,损失越小(如p^=1时损失=0);p^越接近0,损失越大(如p^=0时损失→+∞)。
-
若真实标签y=0(负类),损失简化为−ln(1−p^):逻辑与上述相反。
(2)多分类交叉熵(Categorical Cross-Entropy, CCE)
适用场景:任务输出多个互斥类别(如“数字0-9”“动物猫/狗/鸟”),模型输出层通常用Softmax函数将预测值映射为“各类别概率”(所有类别概率和为1),真实标签需用独热编码(One-Hot Encoding)表示(如“猫”对应[1,0,0],“狗”对应[0,1,0])。
数学公式:
单个样本(C为类别数):
批量样本:
其中,yc∈{0,1}(真实标签的独热编码,仅目标类别为1,其余为0),p^c是模型预测的“类别c的概率”。
核心逻辑:
由于独热编码中仅目标类别![]() 的
的![]() =1,其余为0,损失可简化为
=1,其余为0,损失可简化为![]() ——本质是“惩罚模型对目标类别预测概率过低的情况”。例如,真实类别是“猫”,若模型预测“猫”的概率为0.9,损失=-ln(0.9)≈0.105;若预测概率为0.1,损失=-ln(0.1)≈2.303,惩罚显著。
——本质是“惩罚模型对目标类别预测概率过低的情况”。例如,真实类别是“猫”,若模型预测“猫”的概率为0.9,损失=-ln(0.9)≈0.105;若预测概率为0.1,损失=-ln(0.1)≈2.303,惩罚显著。
2. Hinge损失(Hinge Loss)
适用场景:主要用于支持向量机(SVM)等最大间隔分类模型,目标是“找到一个超平面,使两类样本到超平面的间隔最大”,对异常值的鲁棒性较强。
数学公式(二分类):
单个样本:
其中,y∈{−1,1}(真实标签,区分正负类),f(x)是模型的“原始输出”(未经过Sigmoid/Softmax映射的得分,如SVM中的决策函数值)。
核心逻辑:
-
若y⋅f(x)≥1(样本被正确分类且位于“安全间隔”内),损失=0,模型无需更新。
-
若y⋅f(x)<1(样本分类错误或位于“间隔内”),损失=1 - y⋅f(x),误差越大,损失越大。
特点:不关注预测概率的绝对值,仅关注“样本是否在间隔外被正确分类”,适合对“分类边界稳定性”要求高的场景(如文本分类中的垃圾邮件检测)。
3. 其他分类损失函数
-
Focal Loss:针对“类别不平衡”问题(如癌症检测中,患病样本仅1%,正常样本99%),通过降低“易分类样本”的权重,聚焦“难分类样本”(如模糊的患病样本),公式为:
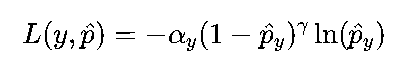
其中αy平衡类别比例,γ调节难样本权重(通常取2),广泛用于目标检测(如RetinaNet)。
-
KL散度损失(Kullback-Leibler Divergence):又称相对熵,衡量“预测分布与真实分布的信息差异”,公式为:
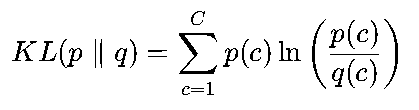
与交叉熵的关系为
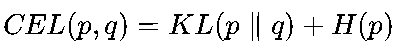 (H(p)是真实分布的熵,为常数),因此在分类任务中,最小化交叉熵与最小化KL散度等价,KL散度更常用于“分布对齐”场景(如生成对抗网络GAN)。
(H(p)是真实分布的熵,为常数),因此在分类任务中,最小化交叉熵与最小化KL散度等价,KL散度更常用于“分布对齐”场景(如生成对抗网络GAN)。
(三)分布匹配损失函数
主要用于衡量“模型生成的分布”与“真实数据分布”的差异,常见于生成模型(如GAN、VAE)、自监督学习等场景。
1. Wasserstein距离(Wasserstein Distance)
别名:Earth-Mover(EM)距离,形象理解为“将一堆土(真实分布)搬运成另一堆土(生成分布)所需的最小工作量”。
数学意义:对于两个分布P(真实)和Q(生成),Wasserstein距离定义为:
其中Π(P,Q)是所有将P映射到Q的运输计划集合,∣∣x−y∣∣是样本x和y的距离。
优势:
-
相比KL散度、JS散度(Jensen-Shannon Divergence),Wasserstein距离即使在两个分布无重叠时也能平滑反映差异(KL/JS散度此时为无穷大或常数,无法指导优化)。
-
生成模型(如WGAN)使用Wasserstein损失时,训练更稳定,不易出现模式崩溃(Mode Collapse)。
2. 对比损失(Contrastive Loss)
适用场景:自监督学习中的“相似性学习”(如人脸识别、图片检索),目标是“让相似样本(正样本对)的特征距离更近,不相似样本(负样本对)的特征距离更远”。
数学公式:
对于样本对(x1,x2),标签y(y=1表示相似,y=0表示不相似),特征向量h1,h2:
其中m是“边界阈值”(如2.0),确保负样本对的距离至少大于m时无损失。
核心逻辑:相似样本对的损失随特征距离增大而增大,不相似样本对的损失仅在距离小于m时存在,强制其远离。
三、损失函数的选择原则
选择合适的损失函数是模型设计的关键步骤,需结合任务类型、数据特性、模型输出形式三大因素综合判断,核心原则如下:
匹配任务类型
-
回归任务(预测连续值):优先选择MSE(无异常值)、MAE(有异常值)、Huber损失(平衡需求)。
-
分类任务(预测离散类别):二分类用BCE+Sigmoid,多分类用CCE+Softmax,类别不平衡用Focal Loss,最大间隔分类用Hinge Loss。
-
生成任务(匹配分布):用Wasserstein损失(GAN)、KL散度(VAE),自监督相似性学习用Contrastive Loss。
考虑数据特性
-
异常值:回归任务避免用MSE,优先MAE/Huber;分类任务可用Focal Loss降低异常样本的影响。
-
类别不平衡:二分类可对BCE加入类别权重(如
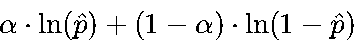 ,α为正类样本占比的倒数),多分类可用加权CCE,或直接用Focal Loss。
,α为正类样本占比的倒数),多分类可用加权CCE,或直接用Focal Loss。 -
标签类型:多分类若标签是“类别索引”(如0,1,2)而非独热编码,需用“稀疏交叉熵损失(Sparse Categorical Cross-Entropy)”,避免独热编码的内存浪费。
结合模型输出
-
模型输出为“概率”:分类任务需搭配BCE/CCE(Sigmoid/Softmax已将输出转为概率)。
-
模型输出为“原始得分”(无概率映射):SVM用Hinge Loss,生成模型用Wasserstein Loss。
四、常见误区与注意事项
“损失越小,模型越好”的局限性
损失函数最小化仅代表“模型在训练数据上的误差最小”,但可能伴随过拟合(训练损失小,测试损失大)。需结合泛化能力指标(如测试集准确率、MAE)评估模型,而非单一依赖训练损失。
损失函数与激活函数的匹配
-
二分类任务:BCE损失必须搭配Sigmoid激活函数(将输出映射到[0,1],确保概率意义)。
-
多分类任务:CCE损失必须搭配Softmax激活函数(确保输出概率和为1)。
-
若模型输出无激活函数(如回归),则直接使用MSE/MAE,无需额外映射。
数值稳定性问题
-
交叉熵损失中,若p^接近0或1,ln(p^)会趋近于−∞或0,可能导致数值溢出。实际实现中(如PyTorch的
nn.BCELoss、nn.CrossEntropyLoss)会内置数值稳定处理(如Clip操作,将p^限制在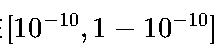 区间),避免直接计算ln(0)或ln(1)。
区间),避免直接计算ln(0)或ln(1)。 -
计算Softmax+CCE时,通常合并为“Softmax交叉熵损失”(如TensorFlow的
tf.keras.losses.CategoricalCrossentropy、PyTorch的nn.CrossEntropyLoss),通过对数恒等变换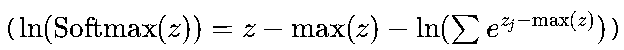 避免指数项ezj因zj过大导致的数值爆炸。
避免指数项ezj因zj过大导致的数值爆炸。
五、损失函数与优化器的协同关系
损失函数定义了“优化目标”,而优化器(如梯度下降、Adam)定义了“如何实现目标”,二者需协同适配,核心关联点如下:
梯度特性匹配
-
若损失函数可导且梯度平滑(如MSE、BCE),可使用收敛速度快的自适应优化器(如Adam、RMSprop),这类优化器能动态调整学习率,适应梯度变化。
-
若损失函数存在不可导点(如MAE、Hinge Loss),建议使用梯度下降(SGD)配合动量(Momentum),或通过次梯度(Subgradient)方法处理不可导点,避免优化器因梯度突变陷入震荡。
损失尺度影响
-
部分损失函数(如MSE)的数值尺度会随样本特征尺度变化(如预测房价时,损失值可能达
 量级),需先对特征标准化(Standardization)或归一化(Normalization),否则优化器可能因梯度过大导致参数更新幅度过大,难以收敛。
量级),需先对特征标准化(Standardization)或归一化(Normalization),否则优化器可能因梯度过大导致参数更新幅度过大,难以收敛。 -
交叉熵损失因基于对数概率,数值尺度相对稳定(通常在0∼10区间),对特征尺度的敏感度低于MSE。
批量大小适配
-
批量损失函数(如批量MSE、批量BCE)的梯度是单样本梯度的平均,批量越大,梯度估计越稳定,优化器(如SGD)收敛越平滑;批量较小时,建议使用Adam等自适应优化器,降低梯度噪声对收敛的影响。
六、典型应用场景的损失函数选择案例
通过具体场景示例,进一步明确损失函数的选择逻辑:
| 应用场景 | 任务类型 | 数据特性 | 推荐损失函数 | 搭配激活函数/优化器 |
|---|---|---|---|---|
| 房价预测 | 回归 | 无明显异常值,误差正态分布 | MSE | 无激活函数 + Adam |
| 极端天气用电量预测 | 回归 | 存在极端值(如台风天用电激增) | Huber Loss(δ=1.5) | 无激活函数 + SGD+Momentum |
| 二分类垃圾邮件检测 | 分类 | 类别平衡(垃圾邮件占比40%) | BCE | Sigmoid + Adam |
| 多分类手写数字识别(MNIST) | 分类 | 类别平衡(10类各占10%) | CCE | Softmax + Adam |
| 癌症影像检测 | 分类 | 类别极不平衡(患病占比1%) | Focal Loss(α=0.25,γ=2) | Sigmoid + Adam |
| 人脸识别(特征相似度学习) | 自监督 | 样本对含相似/不相似标签 | Contrastive Loss(m=1.0) | 特征嵌入层 + Adam |
| 生成对抗网络(WGAN)生成人脸 | 生成 | 真实与生成分布无重叠 | Wasserstein Loss | 生成器/判别器无激活(输出得分) + RMSprop |
七、总结
损失函数是机器学习模型的“核心目标导向”,其选择直接决定模型的学习方向、抗干扰能力与最终性能。核心结论可归纳为三点:
-
任务优先:回归任务聚焦“数值偏差”,分类任务聚焦“分布差异”,生成任务聚焦“分布匹配”,先根据任务类型锁定损失函数大类。
-
数据适配:异常值、类别不平衡、标签类型等数据特性,是从大类中筛选具体损失函数的关键依据(如异常值→MAE/Huber,类别不平衡→Focal Loss)。
-
协同优化:需结合损失函数的梯度特性、数值尺度,搭配适配的激活函数与优化器,避免因“目标与方法不匹配”导致训练失败或收敛缓慢。
理解损失函数的数学本质与适用边界,是从“调参工程师”向“模型设计者”进阶的核心基础。





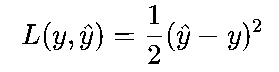

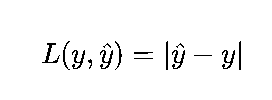
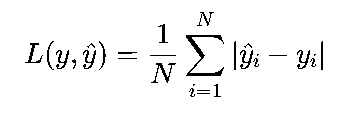
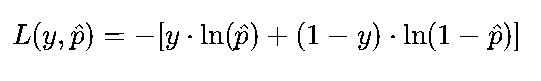
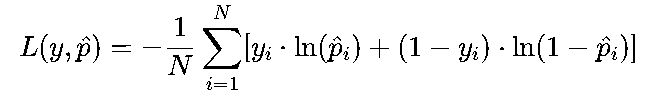
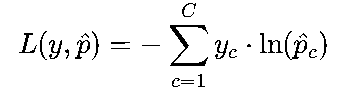
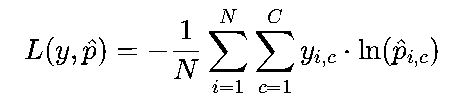
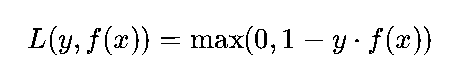
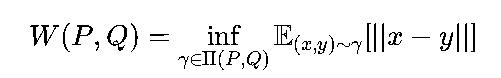
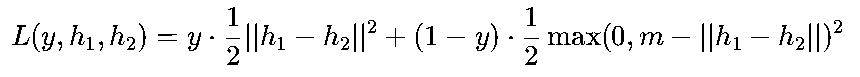
















 1841
1841

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








