字符串匹配算法

转自:http://kofsky.javaeye.com/blog/283247

 

字符串匹配定义：文本是一个长度为n的数组T[1…n], 模式是以个长度m<=n的数组P[1…m]
P和T的元素都是有限字母表∑中的字符

１.字符串朴素匹配
也就是蛮力匹配，每次移动一个步长，然后匹配，时间复杂度O((n-m+1)m)

２.Rabin-Karp算法
Rabin-Karp算法的思想是将模式串P表达为一个值，这样每次进行串匹配的时候，只需要比较这个值就可以了，而不需要对m个字符串进行m次比较。
核心思想是用 一个值 来代替 整个字符串 来参与比较
比如以十进制为例，文本串为'1234567'，模式串为'234'(其值为234),当搜索指针指向第一个字符'1'时,计算出串'123'的值为123，直接与模式串的值234进行比较，不匹配，那么就表明此时模式串匹配失败，将搜索指针移向下一个字符。
如何用　值　来代表　字符串？
想象一下将字符串转换为数值的情形
计算串"123"的值：1*100+2*10+3*1 = 123
    串"6789"的值：6*1000+7*100+8*10+9*1 = 6789
                 
十进制字母表只有0-9，因此选取基数10可以完成的表述整个串
对于Ascii字母表，则可以选取基256。
因此，将一个串表述成一个值是可行的，其时间复杂度为O(m)，其中m为串的长度。
对于文本串T[1…n]，可以在O(m)的时间复杂度计算出前m个字符T[1…m]的值。
而T[2…m+1],T[3…m+2],...T[n-m+1…n]的值，可以在O(n-m)的时间计算出来（动态规划）。
新的问题：值太大，溢出？
通过一个值来表述一个串以后，如果串比较长，那么这个表述串的这个值自然会比较大，而且，可能会溢出。很自然的解决办法是对这个值取模，将它限制到一个固定的范围内。
那么问题又来了，模运算是多对一映射，比如，55和66对11取模后都是0，但是它们的值并不相等。
因此，取模运算会导致一个新的问题，就是伪命中。也就是，模运算匹配，但串本身并不匹配。
可以显式的检查T[i…m+i]与P[1…m]是否相等。
假设计算的值对q取模，倘若q够大，那么T[i…m+i]的值与P[1…m]的值发生伪命中的几率就会比较低，那么额外的测试时间就足够低了。

这样看来，对字符串求值，通过值来进行串的匹配，更像一个启发式的思想，对文本串进行一次过滤，然后在进行逐字匹配。

由于每次在判定模式串是否匹配时，只需要进行一次比较，因此匹配过程中的期望时间复杂度为O(n-m+1)，这个时间没有加上对模式串求值的时间O(m)。最坏是时间复杂度也为O((n-m+1)m)，也就是每一次唯一产生的值都与串的值取模相等，但实际情况下比蛮力匹配要快许多。

3.FA
针对模式串，构造一个有穷自动机，那么，有穷自动机接收的语言就是该模式串匹配的句子。
对于每个模式串，都存在一个字符串匹配自动机，必须在预处理阶段，根据模式构造出相应的自动机后，才能利用它来搜索字符串。构造自动机的核心是构造其状态转移函数。
这种方法功能比较强大，因为它可以搜索以正则式表达的模式串。而其他算法则不能。

4.KMP
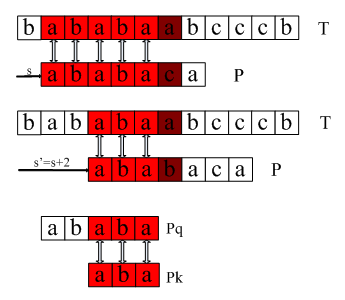
先看一个例子。文本串T为bababaabcccb,模式P为ababaca

。

如图所示。此时，红色的5个字符ababa已经匹配，

从字符c开始不匹配。这时候开始移动模式P。到底该移动几个字符呢？朴素的字符串匹配移动一位，然后重新开始比较。但是根本模式本身的信息，移动s'=s+1是无效的，s'=s+2才有可能导致一个成功的匹配。因为模式P的前5个字符里，ababa的前面三个字符aba同时也是ababa的后缀。也就是说，P的最长前缀同时也是P5的的一个真后缀。这些信息是可以被预先计算的，用前缀函数π来表示。在位移s处有q个字符成功匹配，那下一个可能有效的位移为s'=s+(q-π[q]).

首先假定文本串从第s个位置开始与模式匹配，共匹配q个字符，匹配第q+1个字符时失败，即满足：P[1…q]=T[s+1…s+q]，那么，我们的目标就是，寻找一个位移s'，使得移动1,2,..s'-1都是不可能导致与模式P匹配成功，只有移动s'，才有可能使得与模式P匹配成功。那该怎么寻找这个位移呢？关键就在这个模式本身了。

如果P[1…q]已经匹配成功，在q+1处匹配失败，倘若已知P[1…k]=P[q-k+1…q]（k<q）且k是满足如上等式条件的最大的k,那么，直接移动q-k个位置就可以使得前面的k个字符相匹配。

这个k就包含了模式串本身的信息。它预先被计算，被定义为前缀函数。定义如下：
 
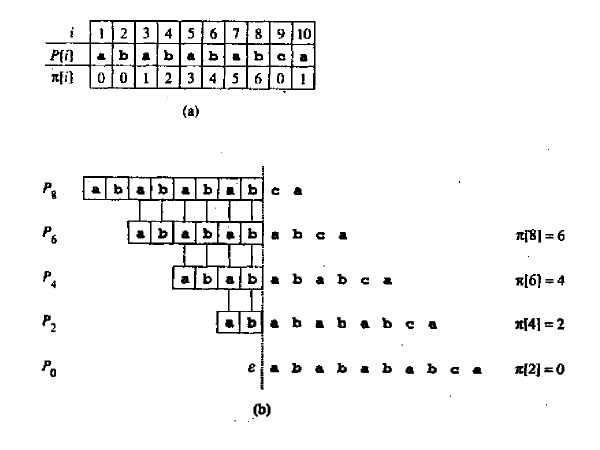
模式P的前缀函数是函数π(0,1,2,...,m-1}→{0,1,2,..,m-1}并满足
π[q]=max{k:k<q且Pk是Pq的后缀,即P[1…k]=P[q-k+1…q]},
π[q]是Pq的真后缀P的最长前缀的长度。

下面是前缀函数的一个计算例子。

计算前缀函数本身就是一个模式串“自我匹配”的过程。KMP的核心也在于通过前缀函数来减少不必要的比较而加快字符串的匹配速度。前缀函数里面包含了模式串的部分匹配信息，也就是当把模式串的前面部分字符移动一段位移后在模式中重复出现，那么这个部分匹配信息就可以用在串匹配中。

也可以看这个，写的还比较详细：
http://jpkc.nwu.edu.cn/datastr/study_online/newsite/pluspage/kmp.htm

5.BM
BM算法有几个要点
1.从右向左进行比较，也就是比较次序为P[m],P[m-1]...
2.当某趟比较中出现不匹配的字符时，BM采用两条启发式规则计算模式串移动的距离，即bad character

shift rule坏字符和good suffix shift rule好后缀规则。
坏字符与好后缀的定义
Index:    0 1 2 3 4 5 6 7 8 9 10 11
Text:     k s e a b c d e f a b c a
Pattern: d e c a b c
           
从右往左进行匹配，第一个mismatch的字符c就是坏字符，后面已经成功匹配的字串abc就是好后缀。
如果字符没有在模式串中

1) 坏字符规则
   P中的某个字符与T中的某个字符不相同时使用坏字符规则右移模式串P，P右移的距离可以通过delta1函数

计算出来。delta1函数的定义如下:
    delta1(x) = 如果字符x在P中未出现，则为 m(模式长度); 否则 m-k, j是最大的整数使得P[k]=字符x，

用数学表达式则为：m - max{k|P[k] = x, 1 <= k <= m};

解释一下，如果字符x在模式P中没有出现，那么从字符x开始的m个文本显然不可能与P匹配成功，直接全部跳

过该区域即可。如果x在模式P中出现，则以该字符进行对齐。

2) 好后缀规则
   P中的某一子串P[j-s+1..m-s]与已比较部分P[j+1..m]相同，可让P右移s位。
   delta2的定义如下：
   delta2（j）= {s|P[j+1..m]=P[j-s+1..m-s])&&(P[j]≠P[j-s])(j>s)}
   （这部分还看得晕乎晕乎的，下次在来完善）

贴个BM例子

 

移动的时候，取两者较大值作为位移值移动。

BM算法在字母表很大，模式串很长时尤其适用，能够显著提高匹配速度。
实际应用中，BM算法比同样具有O(m+n)时间复杂度的KMP算法效率高出3-5倍。具体来说，BM算法的预处理阶段的时间空间复杂性是O(m+n)，查找阶段的时间复杂性是O(mn)，最好情况下的性能是O(n/m)。

参考：
前面几个算法主要参考《算法导论》
BM算法参考
http://www.cs.utexas.edu/users/moore/best-ideas/string-searching/index.html
http://www-igm.univ-mlv.fr/~lecroq/string/node14.html

 

 

 

 

 

 

 

当问题的有效子串只有一个的时候，用KMP：给出1个单词，再给出一段包含m个字符的文章，让你找出这个单词是否在文章里出现过。

有效子串有一大堆的时候，可以用AC自动机（Aho-Corasick automation）：给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。

比较新的，还有一个Sunday算法。比较简单，而且快。

同时，这里有一篇相关介绍论文《一种可做特殊用途的字符串匹配算法》（纪福全 朱战立），可供参考：

字符串匹配就是在一个字符串中查找模式串的一个或所有出现。字符串匹配用途很广泛。例如，在拼写检查、语言翻译、数据压缩、搜索引擎、网络入侵检测、计算机病毒特征码匹配以及DNA序列匹配等应用中，都需要进行字符串匹配。已经提出了许多字符串匹配算法。传统的有BF算法[2,3]、KMP算法[2,3]等，最近提出的有BM算法[2,4]、Sunday算法[2,3]等。

相关算法分析    字符串模式匹配的含义是：在主串S中，从位置start开始查找是否存在模式串（也称作模式串）T，如在主串S中查找到一个与模式串T相同的模式串，则模式串与主串匹配；如在主串S中未查找到一个与模式串T相同的模式串，则不匹配 [1] 。首先作如下假设：

主串S：S[1…N]，长度为N；模式串T：T[1…M]，长度为M；N≥M；

BF算法     BF（Brute Force）算法核心思想是：首先S[1]和T[1]比较，若相等，则再比较S[2]和T[2]，一直到T[M]为止；若S[1]和P[1]不等，则T向右移动一个字符的位置，再依次进行比较。如果存在k，1≤k≤N，且S[k+1…k+M]=T[1…M]，则匹配成功；否则失败。该算法最坏情况下要进行M*(N-M+1)次比较，时间复杂度为O(M*N)。

KMP算法    KMP（Knuth-Morris-Pratt）算法核心思想是：在发生失配时，主串不需要回溯，而是利用已经得到的“部分匹配”结果将模式串右移尽可能远的距离，继续进行比较。这里要强调的是，模式串不一定向右移动一个字符的位置，右移也不一定必须从模式串起点处重新试匹配，即模式串一次可以右移多个字符的位置，右移后可以从模式串起点后的某处开始试匹配。
假设发生失配时，S[i]≠T[j]，1≤i≤N，1≤j≤M。则下一轮比较时，S[i]应与T[next[j]]对齐往后比较：

如T=“abaabcac”，则

BM算法    对于给出的长度为m的模式串T=T&&05;···Tm和主串S=S&&05;···Sn，实现BM算法需要一个辅助数组bm[ ]。它用字符值作为数组的下标，数组的大小依赖于可能出现的字符多少，与模式串的大小无关。对于需要进行中文关键字的匹配，需要扩充ASCII字符集，数组大小则为256。对于任意x属于集合Σ→{1，2，···，256}，bm[x]的值为：

该数组每个字符对应的项记录着该字符在模式串中最后一次出现的位置。BM算法思想是：假如在执行主串位置i起“返前”的一段与模式串T从右向左的字符匹配中，如果模式串T全部字符匹配，则匹配成功；否则需要右移，开始新的一轮匹配，假设匹配不成功发生在模式串中的位置j，由主串匹配不成功字符Si-m+j查找辅助数组得到该字符在模式串T中的最后出现的位置值bm[Si-m+j]。如果bm[Si-m+j]等于零，表示字符Si-m+j不在模式串T中，则模式串跳过该字符，在该字符下一个位置对齐；如果bm[Si-m+j]大于j，表示这个字符在模式串中最后出现的位置在j的左边，则模式串T右移对齐字符Si-m+j；如果bm[Si-m+j]小于j，表示这个字符在模式串中最后出现的位置在j的右边，模式串不能左移，就右移一格。移动量为shift=max(1，m-bm[i-m+j])。

Sunday算法    Sunday算法是Daniel M.Sunday于1990年提出的一种比BM算法搜索速度更快的算法。其核心思想是：在匹配过程中，模式串并不被要求一定要按从左向右进行比较还是从右向左进行比较，它在发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。
假设在发生不匹配时S[i]≠T[j]，1≤i≤N，1≤j≤M。此时已经匹配的部分为u，并假设字符串u的长度为L。如图1。明显的，S[L+i+1]肯定要参加下一轮的匹配，并且T[M]至少要移动到这个位置(即模式串T至少向右移动一个字符的位置)。

图1 Sunday算法不匹配的情况    分如下两种情况：
(1) S[L+i+1]在模式串T中没有出现。这个时候模式串T[0]移动到S[T+i+1]之后的字符的位置。如图2。

图2 Sunday算法移动的第1种情况
(2)S[L+i+1]在模式串中出现。这里S[L+i+1]从模式串T的右侧，即按T[M-1]、T[M-2]、…T[0]的次序查找。如果发现S[L+i+1]和T中的某个字符相同，则记下这个位置，记为k，1≤k≤M，且T[k]=S[L+i+1]。此时，应该把模式串T向右移动M-k个字符的位置，即移动到T[k]和S[L+i+1]对齐的位置。如图3。

图3 Sunday算法移动的第2种情况
依次类推，如果完全匹配了，则匹配成功；否则，再进行下一轮的移动，直到主串S的最右端结束。该算法最坏情况下的时间复杂度为O(N*M)。对于短模式串的匹配问题，该算法执行速度较快。

实验结果     为了评测该算法的性能，随机的抽取一段文本和模式串，并在同一台计算机上用不同的算法进行匹配。测试文本主串S="From automated teller machines and atomic clocks to mammograms and semiconductors,innumerable products and services rely in some way on technology,measurement,and standards provided by the National Institute of Standards and Technology"，模式串T="products and services"。分别用BF算法、KMP算法、BM算法、Sunday算法和ZZL算法在同一台计算机上进行匹配计算，并统计每种算法匹配时总的字符匹配次数。测试结果如表1。
表1 匹配算法实验结果算法：
                                                BF KMP BM Sunday ZZL
一次匹配的总的字符匹配次数 116 95    108 110         23

ZZL是该文作者提出的一个算法：先预处理查找模式串首字符在主串中的所有出现位置，并将其保存在一个数组中。字符串匹配算法就可以从查找到的模式串在主串中的位置开始，匹配模式串首字母之后的其余部分。此时，采用BF算法即可，并可设置一个计数器，记录匹配次数。对于频繁使用的要匹配的主串和模式串来说，由于预先保存了模式串在主串中的所有存储位置，所以ZZL算法的匹配速度会非常快。（前提是已经进行过预处理）