图形学入门学习-GAMES101课程（2）

图形学中几个常用的例子：犹他茶壶、斯坦福兔子、斯坦福龙、康奈尔box。

第十次课

纹理的应用：

In modern GPUs, texture = memory + range query (filtering)
• Environment lighting (用四个面记录、用一个球记录、用一个立方体记录)
• Store microgeometry 微分几何
• Procedural textures 过程纹理
• Solid modeling 实物造型
• Volume rendering 体渲染
纹理可以记录任何属性，可以不是颜色，比如高度、法向量等。
复杂表面需要更多的Triangle，也可以使用纹理解决（模型不够贴图凑）。
Bump / normal mapping 凹凸/法线贴图，通过高度贴图计算法向量，伪造几何表面。

Displacement mapping 位移贴图，按照高度贴图移动了点的位置，真实地改变了面的凹凸性。

介绍了很多隐式几何的例子

两种表达：implicit geometry和explicit geometry。
隐式几何：algebraic surface(方程式)； level sets(水平集)； distance functions(距离函数)；Constructive Solid Geometry(构造实体几何)。
显式几何：point cloud； polygon mesh； subdivision。
各种方法有不同的优点，适应性不同。

第十一次课

几何的显式表示例子：explicit representations：
curve：Bezier curves; De Casteljau’s algorithm; B-splines.
surfaces: Bizier surfaces; Triangles & quads (subdivision, simplification, regularization).

point cloud

列举物体表面的点，是最简单的表示方式，可以表示任意物体；适用于大数据集；经常转换为多边形网格；在下采样的地方很难画出来。

polygon mesh

需要存储点和多边形，需要复杂的数据结构；易于对网格进行细分、简化和规范化。
不同的存储方式对应了不同的文件，例如.obj, .off, .mesh, .stl等。

curve

贝塞尔曲线：包含n个控制点，例如上图就是一个三次方贝塞尔曲线，p0和p3分别为起点和终点，定义一个参数$t\in [0,1]$，在向量$p_0{p}_1,p_1{p}_2,p_2{p}_3$上分别取t处的点，连接后得到两条线段，继续取t出的点，连接之后就得到了参数t对应的点。可以理解为使用线性插值的方法去电，递归操作。
三次方贝塞尔曲线的表达式：$$B(t)=(1-t{)}^3{P}_0+3(1-t{)}^{2}t{P}_1+3(1-t)t^2{P}_2+t^3{P}_3,t\in [0,1]$$
该公式通过给定的控制点的坐标计算出了曲线上参数t对应的点的坐标。其中每个控制点的系数就是伯恩斯坦多项式(Bernstein polynomials)，其伯恩斯坦形式图形如下：
$$B^n(t)=\sum _{i=0}^n{B}_i^n{P}_i,t\in [0,1],n是控制点的个数,B_i^n是伯恩斯坦多项式$$

矢量字体就是使用贝塞尔曲线和绘图指令表示的。
贝塞尔曲线的性能：

1. 起点和终点的坐标和切线方向是确定的；
2. 各项系数之和为1
3. 对称性和递归性
4. 仿射变换性质：可以通过控制点来变换曲线，在几何上对贝塞尔曲线做仿射变换相当于对其控制点做仿射变换再求对应的贝塞尔曲线；
5. 凸包属性(曲线在控制点的凸包内)。

分段贝塞尔曲线 Piecewise Bezier Curves
$n$非常大的贝塞尔曲线很难控制，所有就需要分段了。那怎么分段呢？为了段和段之间平滑过渡，前一段的终点和后一段的起点保证切向量一致。
关于连续性G1 G2 G3的区别
描述曲线、曲面的连续方式，以及平滑程度。
G0：曲线无断点，曲面无缝隙无孔洞；
G1：一阶导数$dy/dx$连续；
G2：曲率(单位弧段上切线转过的角度大小)$d\alpha /ds$连续；对曲线做曲率分析，曲率曲线连续无断点，对曲面做斑马线分析，斑马线平滑无尖角。
G3：曲率相切连续；对曲线做曲率分析，曲率曲线连续且平滑无尖角，即一阶导数连续。

C0、C1、C2连续应该是指0-1-2阶导数连续。
关于光顺性

样条：可控的曲线
B样条：可以理解为对贝塞尔曲线的扩展，贝塞尔曲线如果其中一个控制点移动了，整个曲线都改变了。我们需要一种较好的局部性质。

贝塞尔曲面

http://netclass.csu.edu.cn/NCourse/hep089/Chapter3/CG_Txt_3_019.htm
四条贝塞尔曲线，分别通过参数$u$确定四个点，然后以这四个点为控制点确定一条贝塞尔曲线，好多曲线就构成了一个曲面。

第十二次课

Mesh Subdivision 网格细分

增加点，产生更多的三角形，改变新增点和原有点的位置。
Loop Subdivision
Split each triangle into four；Assign new vertex positions according to weights New / old vertices updated differently。
内部新点和边界新点的位置计算：

旧点中内部点和边界点的位置更新：

Catmull-Clark Subdivision
Loop Subdivision 只能细分三角形网格，而 Catmull subdivision 可以对一般的网格细分。


经过一次操作之后，奇异点的个数加倍；之后的操纵不会影响奇异的的个数。

Mesh Simplification 网格简化

Collapsing An Edge
将一个面简化为一个point：每个face计算一个Quadric Error Metrics (二次度量误差)，通过这个数的大小判断这个face是否要简化。

Mesh Regularization 网格标准化

Shadow Mapping

判断某个点是否为影子：观察两次，第一次从eye视角看，每个点记录depth，通过变换把这个depth转换为光源视角下的depth，和实际光源视角下的该点的depth比较，如果前者更大那么该点为影子。

Visualizing Shadow Mapping
问题：实际光源不是点光源，影子是软阴影。

• Hard shadows (point lights only)
• Quality depends on shadow map resolution (general problem with
  image-based techniques)
• Involves equality comparison of floating point depth values means
  issues of scale, bias, tolerance

第十三次课

光栅化对一些全局属性不友好，例如软阴影、光的反射不止一次。
光栅化比较快，但是质量低；光线追踪计算量很大，很慢，多用于离线渲染。
Rasterization: real-time, ray tracing: offline。

Recursive (Whitted-Style) Ray Tracing：光线是可逆的，从眼睛或者相机向每一个像素方向发射一束光线，经过物体的反射/折射到达光源。

那么如何求光线和三角形的交点呢？
光线的表示：$r(t)=o+td,0<t<1。o表示起点，d是单位向量，t表示传播时间$
与三角形求交点可以转化为和平面求交点，然后判断该点是否在三角形里面。

有没有更快的求解方法呢？

关键问题是这样做计算量非常大，如何加速计算？
用一个Bounding Volumes(包围盒)把物体框起来，这样如果光线没有穿过包围盒就不用判断里面的三角形。
常用的是Axis-Aligned Bounding Box (AABB)(轴对⻬包围盒)，便于计算。那么如何计算光线是否经过包围盒呢？
将一个立方体看成三个对面的交集，先计算光线与每个对面的交点得出三对$t_{min}和t_{max}$(光线进出一个对面的时间)，然后求交集就是光线在包围盒里面的时间。
$t_{enter}=max(t_{min}),t_{exit}=min(t_{max})$
当且仅当$t_{enter}<t_{exit}并且t_{exit}>0$，光线穿过AABB形包围盒。（如果$t_{enter}<0并且t_{exit}>0$则光线的起点在包围盒内）
下图是一个二维的例子：

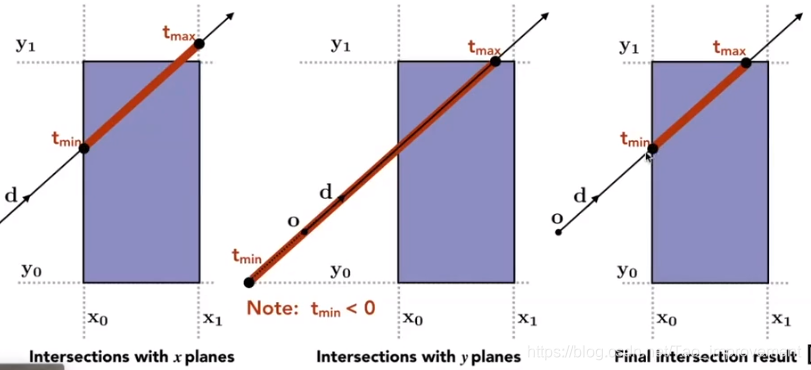
第十四次课 加速求交

思想：将一个大的包围盒(包含好多物体)划分成很多小的包围盒；如果均匀划分，由于某些区域物体稀疏而某些区域物体密集，加速效果并不好，另外一个物体可能会处在不同的几个包围盒中，这也不太好；于是就基于物体个数，每次划分尽量使得两部分包含的物体个数一致。

Uniform Grids 均匀网格

缺点：
网格划分多少合适呢？根据经验，$cells=C\ast objs(物体个数),C\approx 27in3D$
对于物体均分分布的画面效果不错，但是对于物体分布某处很密集而某处很稀疏的画面效果很不好。采用空间划分方法解决这个问题，Spatial Partitioning Examples：Oct-Tree, KD-Tree, BSP-Tree.

Oct-Tree

上图其实是一个二维空间的四叉树结构。三维空间才是一个八叉树，那么$n$维空间就是$2^n$叉树，太复杂了。

BSP-Tree

三维空间需要用一个平面切分，不容易处理。

KD-Tree

依次划分每个维度(沿着x轴一分为二，沿着y轴一分为二，…x,y,…)，结果就类似于二叉树。与光线求交，先判断光线与A是否相交，若相交，判断与1是否相交(若相交，判断光线与1中每个物体是否相交)，然后递归B。
问题：一个物体可能处在多个盒子中，那么一个三角形也可能处在多个盒子中，这时候就三角形和光线是否相交就很难(例如：Triangle的三个顶点都不在盒子中，但是它和盒子相交)。

Object Partitions & Bounding Volume Hierarchy (BVH) 物体划分BVH

BVH是目前广泛使用的结构，通过物体个数划分，依次划分每个维度。二维情况如图：

找到一个包围盒，递归将其分成两个子集并重新计算子集的包围盒，在某一条件下停止。所有的物体都处在叶子节点中。
划分子集的时候，最好是两个子集包含的物体个数尽量相同，保证是一个平衡树。做法是计算每个三角形的重心，然后找出中位数。快速选择算法。

第十五次课

Radiometry 辐射度量学

还记得在Blinn-Phong模型中的 light intensity $I$, 它没有单位。
Measurement system and units for illumination
Accurately measure the spatial properties of light
New terms: Radiant flux, intensity, irradiance, radiance

intensity, irradiance, radiance

单位时间单位立体角的能量；单位面积的能量；单位立体角单位面积的能量。
https://www.bilibili.com/read/cv6938495/

Bidirectional Reflectance Distribution Function (BRDF) 双向反射分布函数

represents how much light is reflected into each outgoing direction $w_r$ from each incoming direction



对反射方程的理解：

人眼看到的 = 物体自身发光量 + 每个面光源经过物体反射的光量

另一种理解方式：经过复杂的简化推导，人眼看到的 = 物体自身发光量 + 一次弹射的光 + 二次弹射的光 + …
类似于泰勒展开，实际上不需要计算那么多分量就可以近似。

第十六次课

对于定积分，某些函数很难计算，采用蒙特卡洛积分近似。对自变量进行采样，然后求和；采样可以是均匀的，也可以不是，有很多研究。下面式子中的$p$表示概率密度函数。

Whitted-Style Ray Tracing 存在的问题：对于光滑镜面和磨砂镜面都是执行了镜面反射；没有考虑光线弹射。


假设每个pixel采样100个点，计算直接光照需要100次计算，而计算间接光照(二次弹射)需要10000次，这样计算量就很大。

于是 路径追踪(Path Tracing) 应用而生

如果只考虑一条光线，计算量就不会翻倍。这就是Path Tracing。
而对于递归的终止条件我们采用俄罗斯轮盘赌(Russian Roulette (RR))思想，其实就是以一定概率终止。
只考虑一条光线，每次随机方向，那么势必有很大的噪声。而每次随机选择一个方向进行path tracing，会造成很大一部分ray打在空旷的地方而浪费计算量。我们之前考虑的是采样一个pixel，如果采样光源呢？

假设光源是一个面光源，建立$dw和dA$之间的换算关系，就可以将之前的着色方程用到光源上。

以前我们说的 Ray Tracing 就是指 Whitted-style ray tracing；而现在的光线追踪包含了一般的light transport、path tracing、photon mapping、Metropolis light transport、VCM / UPBP…
没有讲到的问题：
如何采样一个函数？
蒙特卡洛积分选择哪种概率密度函数(pdf)更好？importance sampling
随机数的产生方法有没有好坏之分呢？low discrepancy sequences
采样pixel的半球面和采样光源两种方法能否结合？multiple imp. sampling
从pixel发出的不同path，得到radiance，为什么取平均？要不要加权？(pixel reconstruction filter
如何将radiance换算成颜色？gamma correction, curves, color space

第19次课 cameras、lenses、light fields

一幅图像的来源可能是synthesis或者capture，而capture的主要设备是相机。

成像原理

相机的原理就是小孔成像。如果这个孔太大，成像平面的一个点就会是来自物体不同位置的多个光子的叠加，像就很模糊，甚至无法成像。如果孔太小，通过的光线就会少，像的亮度也会降低。而且孔太小还会发生衍射等反应，这也会对成像有影响。

相机成像使用的是透镜，根据高斯成像公式$1/u+1/v=1/f$，就有了下图。
物体上的一个点的光子通过任意方向穿过透镜之后会在成像平面汇聚到同一个点。
照片上的每一个像素记录的是irradiance信息。

相机的构成：镜头、光圈、快门、感光元件sensor。

视场 Field of View（FOV）

$FOV=2arctan(\frac{h}{2f})$

视场角同时受胶片大小和焦距的影响，为了方便表示，通常使用35mm(36 x 24mm) 格式的胶片为基准，那么焦距越大，视场角就越小。17mm焦距对应的正好是水平视角。
通常我们说手机相机的焦距是28mm，意思是保持视场角大小不变，将底片大小缩放为35mm对应的焦距是28mm。

曝光度

$Exposure=time\ast irradiance$
time 由快门(shutter speed)决定， irradiance 由光圈(aperture size)大小决定。另外，后期可以通过感光度(ISO gain)调节亮度。


shutter speed、aperture size、ISO gain分别会引起上图所示的问题。

• 光圈太大会引起景深，背景模糊现象。
• 快门太慢会引起运动模糊，即运动速度大于快门速度。
• 感光度太大，会放大噪声。
• 对于机械快门，打开有一个过程，太慢会导致一些扭曲现象，如图中的螺旋桨。
  这里光圈大小使用了F-number表示，F数是光圈直径的倒数。
  
  

高速摄影和长曝光摄影(延迟摄影)都很有意思。所谓高速摄影就是调小快门时间，调大光圈。所谓延迟摄影就是调大快门时间，曝光一段时间。

弥散圆Circle of Confusion (CoC)

假设前景在focal plane的位置，成像就在sensor plane，很清晰，而背景object成像之后是一个圆形区域，不是一个点，这个圆形区域就称为Circle of Confusion。COC大小的计算公式如图，COC受光圈大小的影响。

第20次课 Color and Perception

Light Field / Lumigraph

The Plenoptic Function（全光函数）

简单来说，光场描述空间中任意一点向任意方向的光线的强度。而完整描述光场的全光函数是一个7维函数，包含任意一点的位置$(Vx,Vy,Vz)$，任意方向(极坐标中的$\theta ,\varphi$)，波长($\lambda$)和时间($t$)。


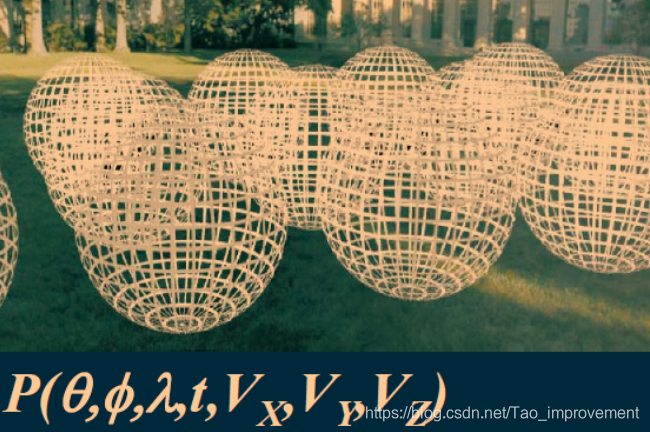
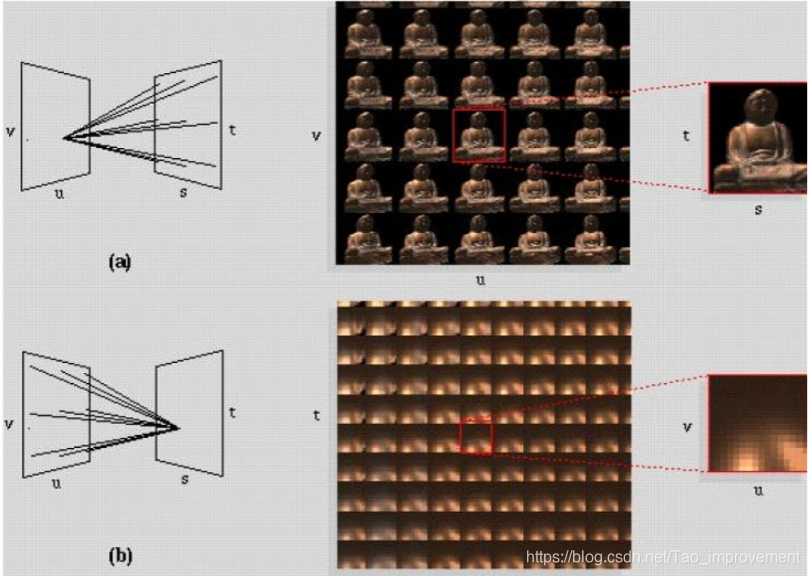
实际上，颜色和时间通常是由RGB和帧来表示，我们只关注位置和方向，此时可以简单地使用两个平面表示光场。
使用这两个平面上的两个点就可以包含位置和方向信息，只是限制于平面的大小，描述的光场范围有限。我们使用相机阵列记录光场，其原理仍然是传统的成像系统，只是在各个位置$(u,v)$拍摄朝向每一个$(s,t)$的颜色信息，然后组织起来。图b可以看成是记录了radiance信息，即从不同位置看向同一个$(s,t)$。

光场照相机Lytro

在传感器表面覆盖一层透镜阵列，把原本的一个像素(irradiance)分开成多个像素(radiance)记录下来。Each pixel (irradiance) is now stored as a block of pixels (radiance) 。这样拍下来的全光照片可以后期调整焦距等参数。

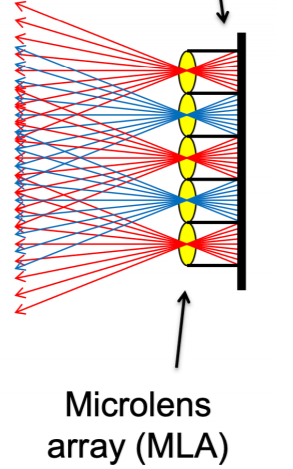
缺点是这样做增加角度分辨率的同时损失了像素分辨率；微透镜的涉及很复杂，所以成本很高。

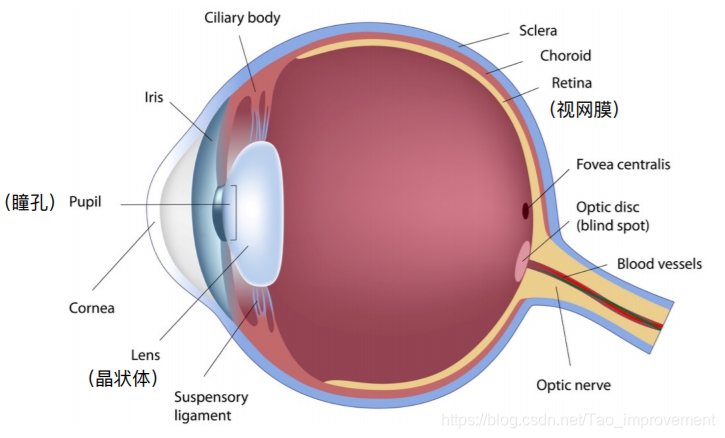
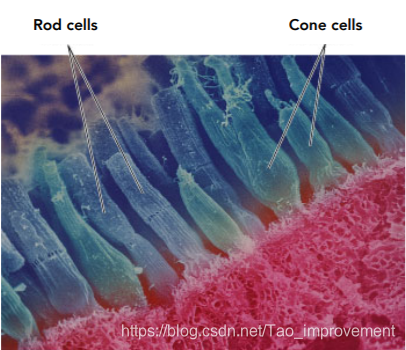
Physical Basis of Color

光线按波长分开，用功率谱密度函数Spectral Power Distribution (SPD)表示各个波长的分量。物质发射、吸收或散射的不同波长的情况用光谱表示，那么物体的光谱和打在它上面的光的SPD共同决定了我们看到的颜色。由于不同个体的感光细胞数量不一样，不同的动物所看到的颜色是不同的，不同的人所感受到的颜色也是不同的。

加色系统、加色匹配实验

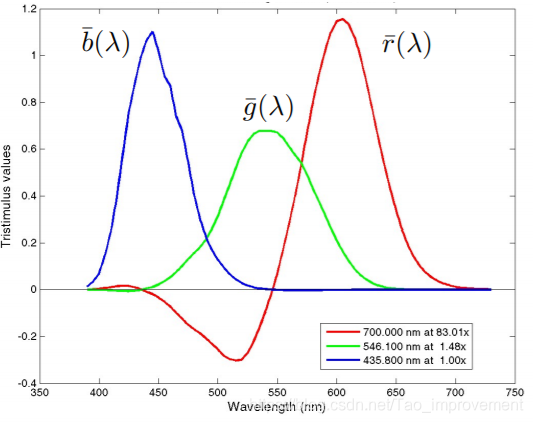
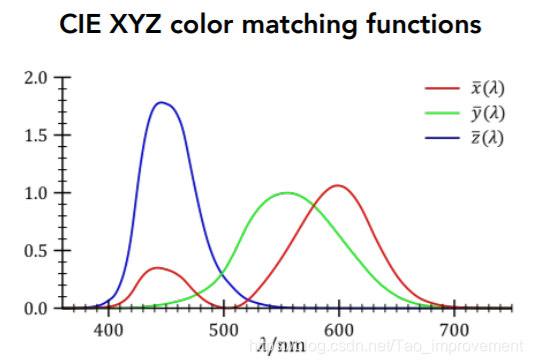
CIE RGB Color Matching Functions
通过实验测试得到了这个颜色匹配函数，即RGB分量按比例叠加以模拟不同的波长。之所以存在负数是因为某些波长对应的颜色叫加不出来，需要做减法。

对于任意物体，有了它的光谱之后，就可以使用下面的积分计算出它的RGB颜色分量。

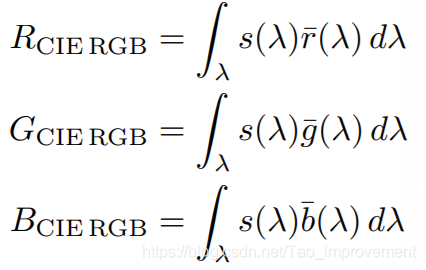
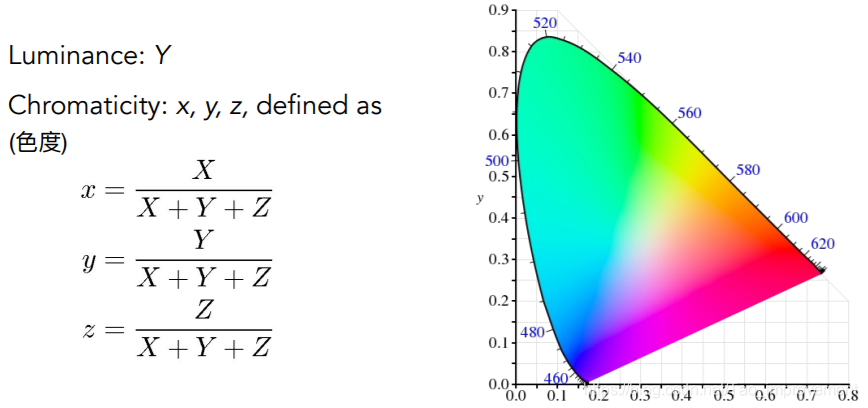
Color Spaces

上面其实已经介绍了sRGB。
更通用的XYZ颜色空间。x和z就可以表示该空间的所有颜色，y表示的是亮度信息。便于展示色域。


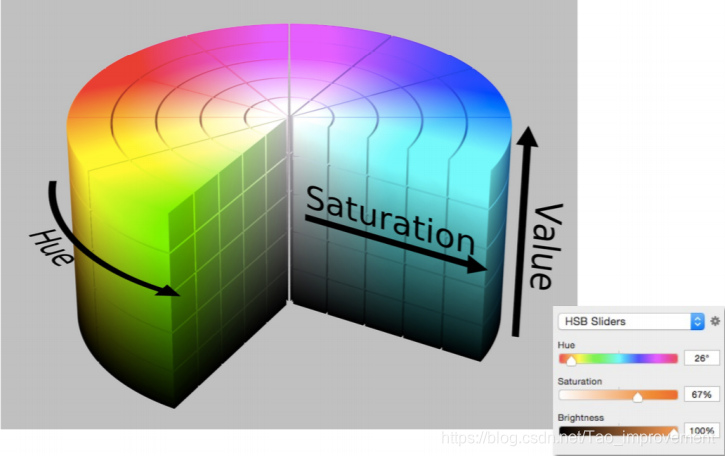
HSV颜色空间，很容易理解。颜色拾取器就是用的这个。
Hue色调，saturation饱和度，value亮度。

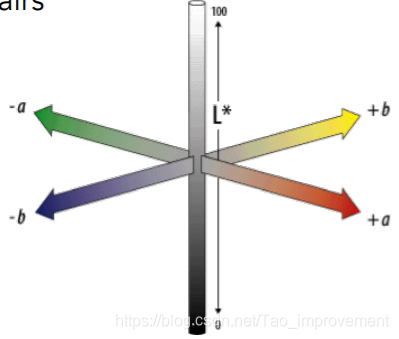
还有Lab颜色空间，利用了互补色。

CMYK减色系统，用于打印，中间是黑色。
虽然CMY可以表示K，但是因为黑色很常用而且混合成本高就保留了。

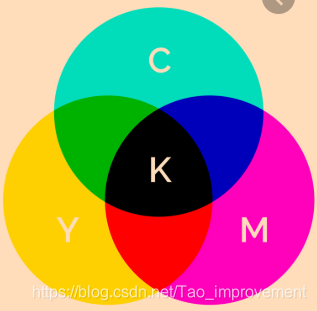
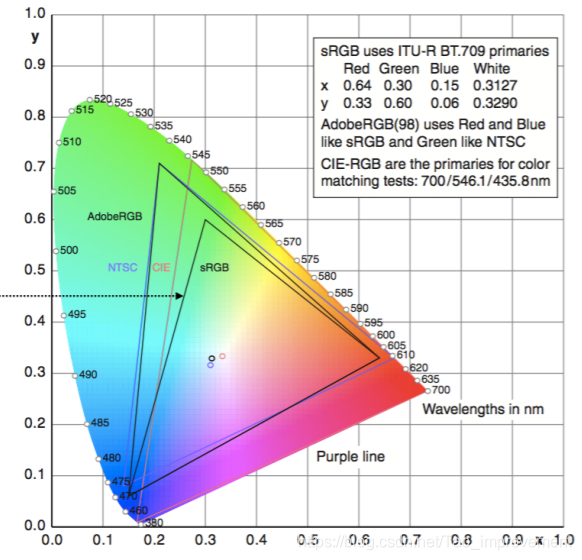
色域Gamut

不同颜色系统的色域不同，边缘是纯色，中心是白色。