吴恩达Deeplearning.ai之1-3:浅层神经网络

这篇笔记主要是关于浅层神经网络的，包含以下内容：

目录

1. 神经网络的表示(Neural Network Represetation):

2. 计算神经网络的输出(Computing a Neural Network's Output):

3. 多样本的向量化(Vectorizing across multiple example):

4. 向量化实现的解释(Explanation for vectorized implementation):

5. 激活函数(Activation functions):

6. 为什么需要非线性激活函数(Why  do you need non-linear activation function):

7. 神经网络的梯度下降法(Gradient Descent for neural network):

8. 随机初始化(Random Initialization):

1. 神经网络的表示(Neural Network Represetation):

单个神经元的结构可以看成是一个逻辑回归模型，如下：

                                                                 

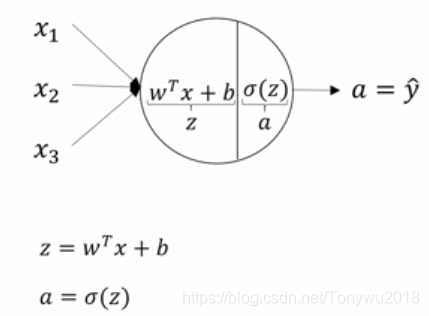
   一个简单的双层神经网络如下：

                                                    

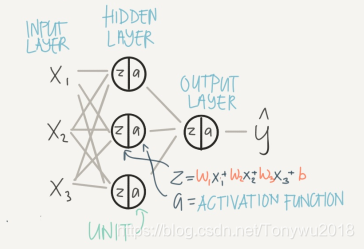
其中所在的层为输入层，通常输入层不计入神经网络层数的数目，第一层为隐藏层，在这一层有3个神经元(节点)，每个神经元中都有一个激活函数，第二层为输出层只包含一个神经元，用来对最后结果进行预测。

神经网络中前一层为输入，后一层为输出，两层之间需要用参数连接计算。

输入层和隐藏层之间的参数矩阵为：

：其中[]上标表示第几层的参数，此处为第一层的参数，第一个3为隐藏层的神经元的个数；第二个3为为输入层神经元的个数

:第一个数为隐藏层的神经元的个数，第二个数为1。

隐藏层和输出层之间的参数矩阵为：

：1为输出层的神经元数，3为隐藏层的神经元数。

：1为输出层的神经元数。

2. 计算神经网络的输出(Computing a Neural Network's Output):

                

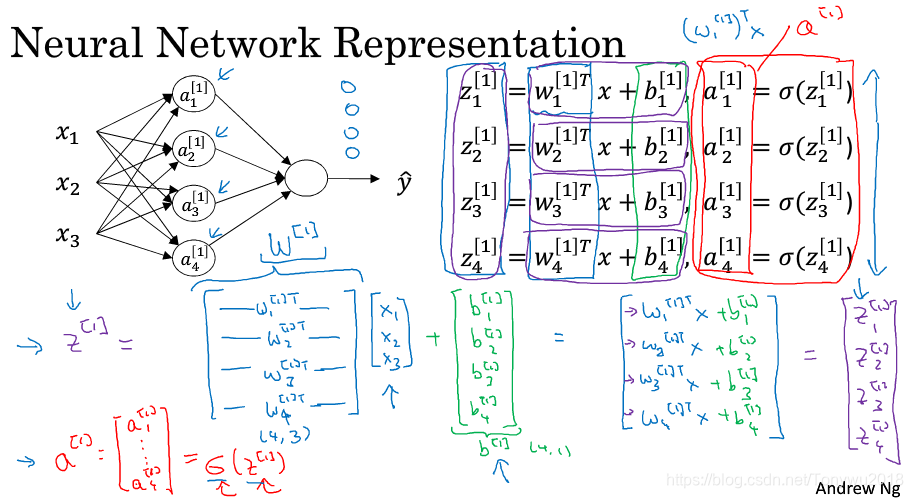
:其中上标表示第层，下标表示第个神经元，向量化后的表达式如下：

                 

3. 多样本的向量化(Vectorizing across multiple example):

上一小节是讲述的单个样本的向量化，本小节是m样本的向量化。

                 

类比于逻辑回归中的形式，可以对m个样本按行进行堆叠，从而避免了使用for循环。

4. 向量化实现的解释(Explanation for vectorized implementation):

向量化的证明如下：

                 

               

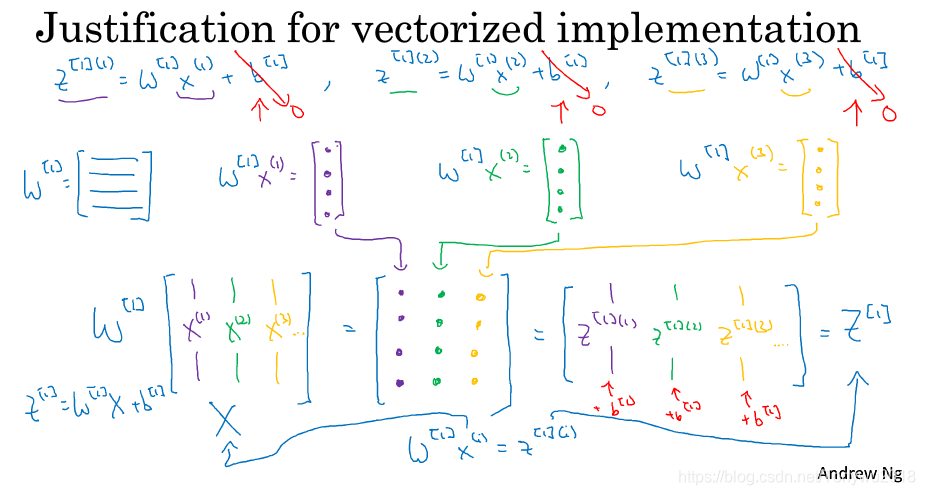
最终上图中左上角的两层神经网络可以被向量化为右下角的四个式子。

5. 激活函数(Activation functions):

前面的章节中使用的激活函数都是Sigmoid函数，实际上很多情景下使用Sigmoid函数作为激活函数并不是最优的，在本小节将会介绍其他的常用的激活函数。其它常用的激活函数如下：

                    

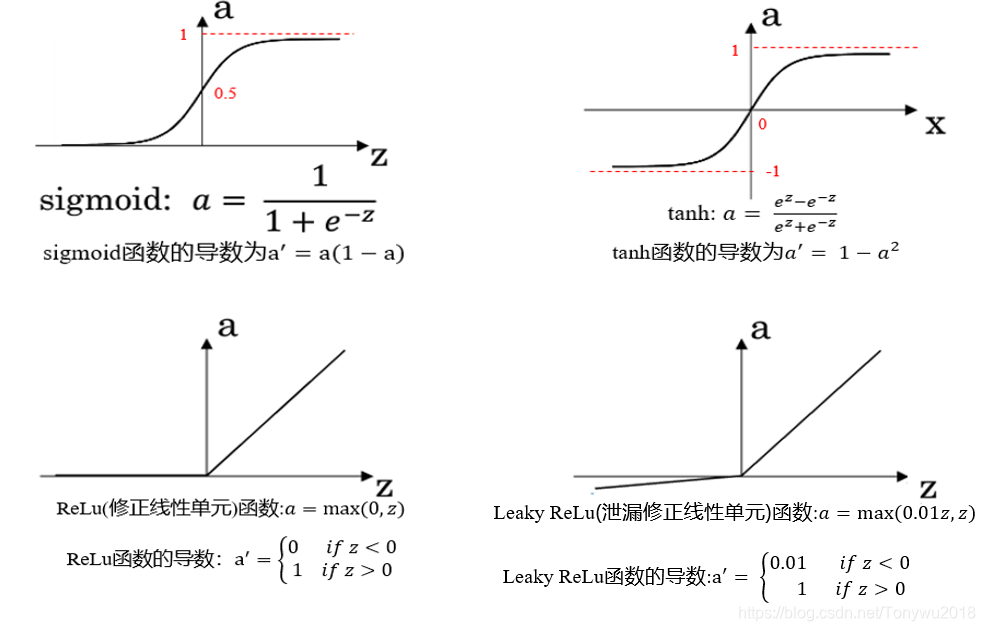
对于这几种激活函数，该如何选择呢。

sigmoid函数和tanh函数：

从图像中可以看到，sigmoid函数值域为[0,1]，而tanh函数的值域为[-1,1]，所以sigmoid函数的分布的均值在0.5附近，而tanh函数的分布的均值在0附近，这就类似于归一化，所以tanh函数作为激活函数比sigmoid函数有更好的效果。也不是说不会用到sigmoid，通常在二分类问题中，sigmoid函数一般作为输出层的激活函数。

ReLu函数：

可以看到，无论是sigmiod函数还是tanh函数，当比较大的时候，函数切线的斜率都比较小，这就大大降低了梯度下降的速度，ReLu函数就很好的弥补了这一点，当z的取值大于0时，函数切线的斜率始终为1，当z的取值小于0时，切线的斜率始终为0，这可以一定程度上让网络变的稀疏，防止过拟合的现象发生。由于ReLu函数在z大于0时的导数始终为1，这使得ReLu函数作为激活函数不会产生梯度消失的现象，同时也使得在反向传播求误差导数时，计算变的更加简单。

Leaky ReLu函数：

Leaky ReLu函数在ReLu函数上做了微小的修改，即在z小于0时，函数不为0，而是有很小的斜率。

既然ReLu函数有这么好的性质，那我们为何不让z小于0时，斜率也为1，即用线性函数作为激活函数，这将在下一小节进行说明。 

6. 为什么需要非线性激活函数(Why  do you need non-linear activation function):

上面提到为什么不用线性函数作为各层的激活函数。实际上如果用线性函数作为激活函数的话，那么线性函数的线性组合还是线性函数(只是前面的系数不同而已)，所以无论你的神经网络有多少层，它的效果是和一个线性分类器是一样的，显然这是不可取的。尽管可以在神经网络的输出层使用线性函数作为激活函数，但是通常不会这么做。

激活函数的非线性是多层神经网络的基础，其保证了多层网络不会退化成单层线性网络。有关激活函数的更多的相关知识，可以参考这篇文章。

7. 神经网络的梯度下降法(Gradient Descent for neural network):

神经网络的反向传播的推导如下：

                        

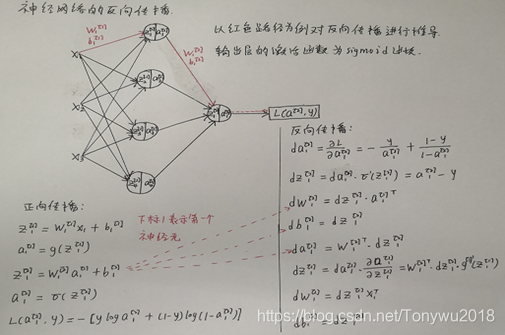
将单样本的反向传播向量化得到m个样本的反向传播：

                    

8. 随机初始化(Random Initialization):

在进行训练网络之前，通常要初始化权重矩阵和偏置向量，那么权重矩阵的初始值怎么设置就成为了一个关键的问题。在逻辑回归中，可以将权重矩阵初始化为全0矩阵，但是在神经网络中，这是不可取的。以下面的网络为例进行说明：

                                                                    

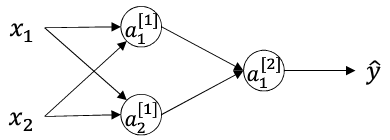
有上面的网络可以得知权重矩阵的维度为(2,2)，若将其初始化为：

                                                                               

那么、，由于同层的激活函数是一样的，所以有，结果发现，同一层的两个神经元做的是完全相同的计算，效果是和单个神经元是一样的。实际上，不仅仅是权重矩阵初始化为全0矩阵时会产生这种现象，初始化为全1矩阵，全0.1矩阵等等都会导致这一层的神经元进行相同的计算。

所以在神经网络中，通常会对权重矩阵进行随机初始化，用python语句表示如下：

import numpy as np
W = np.random.rand((2,2))*0.01   # 随机生成服从高斯分布的2*2的矩阵

为什么在随机数矩阵后*0.01，这是因为激活函数sigmoid和tanh在较大时具有饱和性，即较大时函数的导数很小，以至于使梯度下降的速度变的很慢，为了避免发生这种情况，通常使用较小的值对权重矩阵进行随机初始化。