动态规划相信大家都知道,动态规划算法也是新手在刚接触算法设计时很苦恼的问题,有时候觉得难以理解,但是真正理解之后,就会觉得动态规划其实并没有想象中那么难。网上也有很多关于讲解动态规划的文章,大多都是叙述概念,讲解原理,让人觉得晦涩难懂,即使一时间看懂了,发现当自己做题的时候又会觉得无所适从。我觉得,理解算法最重要的还是在于练习,只有通过自己练习,才可以更快地提升。话不多说,接下来,下面我就通过一个例子来一步一步讲解动态规划是怎样使用的,只有知道怎样使用,才能更好地理解,而不是一味地对概念和原理进行反复琢磨。
首先,我们看一下这道题(此题目来源于北大POJ):
数字三角形(POJ1163)
在上面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可,不必给出具体路径。 三角形的行数大于1小于等于100,数字为 0 - 99
输入格式:
5 //表示三角形的行数 接下来输入三角形
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
要求输出最大和
接下来,我们来分析一下解题思路:
首先,肯定得用二维数组来存放数字三角形
然后我们用D( r, j) 来表示第r行第 j 个数字(r,j从1开始算)
我们用MaxSum(r, j)表示从D(r,j)到底边的各条路径中,最佳路径的数字之和。
因此,此题的最终问题就变成了求 MaxSum(1,1)
当我们看到这个题目的时候,首先想到的就是可以用简单的递归来解题:
D(r, j)出发,下一步只能走D(r+1,j)或者D(r+1, j+1)。故对于N行的三角形,我们可以写出如下的递归式:
根据上面这个简单的递归式,我们就可以很轻松地写出完整的递归代码:
对于如上这段递归的代码,当我提交到POJ时,会显示如下结果:
对的,代码运行超时了,为什么会超时呢?
答案很简单,因为我们重复计算了,当我们在进行递归时,计算机帮我们计算的过程如下图:
就拿第三行数字1来说,当我们计算从第2行的数字3开始的MaxSum时会计算出从1开始的MaxSum,当我们计算从第二行的数字8开始的MaxSum的时候又会计算一次从1开始的MaxSum,也就是说有重复计算。这样就浪费了大量的时间。也就是说如果采用递规的方法,深度遍历每条路径,存在大量重复计算。则时间复杂度为 2的n次方,对于 n = 100 行,肯定超时。
接下来,我们就要考虑如何进行改进,我们自然而然就可以想到如果每算出一个MaxSum(r,j)就保存起来,下次用到其值的时候直接取用,则可免去重复计算。那么可以用n方的时间复杂度完成计算。因为三角形的数字总数是 n(n+1)/2
根据这个思路,我们就可以将上面的代码进行改进,使之成为记忆递归型的动态规划程序:
当我们提交如上代码时,结果就是一次AC
虽然在短时间内就AC了。但是,我们并不能满足于这样的代码,因为递归总是需要使用大量堆栈上的空间,很容易造成栈溢出,我们现在就要考虑如何把递归转换为递推,让我们一步一步来完成这个过程。
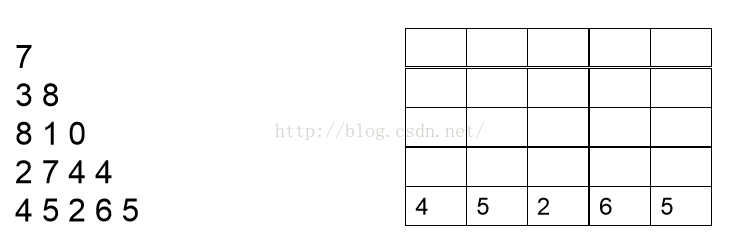
我们首先需要计算的是最后一行,因此可以把最后一行直接写出,如下图:
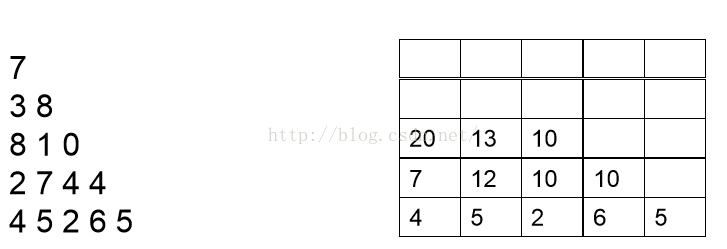
现在开始分析倒数第二行的每一个数,现分析数字2,2可以和最后一行4相加,也可以和最后一行的5相加,但是很显然和5相加要更大一点,结果为7,我们此时就可以将7保存起来,然后分析数字7,7可以和最后一行的5相加,也可以和最后一行的2相加,很显然和5相加更大,结果为12,因此我们将12保存起来。以此类推。。我们可以得到下面这张图:
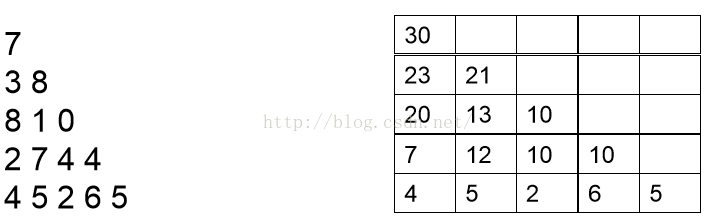
然后按同样的道理分析倒数第三行和倒数第四行,最后分析第一行,我们可以依次得到如下结果:
上面的推导过程相信大家不难理解,理解之后我们就可以写出如下的递推型动态规划程序:
我们的代码仅仅是这样就够了吗?当然不是,我们仍然可以继续优化,而这个优化当然是对于空间进行优化,其实完全没必要用二维maxSum数组存储每一个MaxSum(r,j),只要从底层一行行向上递推,那么只要一维数组maxSum[100]即可,即只要存储一行的MaxSum值就可以。
对于空间优化后的具体递推过程如下:
接下里的步骤就按上图的过程一步一步推导就可以了。进一步考虑,我们甚至可以连maxSum数组都可以不要,直接用D的第n行直接替代maxSum即可。但是这里需要强调的是:虽然节省空间,但是时间复杂度还是不变的。
依照上面的方式,我们可以写出如下代码:
接下来,我们就进行一下总结:
递归到动规的一般转化方法
递归函数有n个参数,就定义一个n维的数组,数组的下标是递归函数参数的取值范围,数组元素的值是递归函数的返回值,这样就可以从边界值开始, 逐步填充数组,相当于计算递归函数值的逆过程。
动规解题的一般思路
1. 将原问题分解为子问题
- 把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题都解决,原问题即解决(数字三角形例)。
- 子问题的解一旦求出就会被保存,所以每个子问题只需求 解一次。
2.确定状态
- 在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状 态”。一个“状态”对应于一个或多个子问题, 所谓某个“状态”下的“值”,就是这个“状 态”所对应的子问题的解。
- 所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。
整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次,且在每个状态上作计算所花的时间都是和N无关的常数。
3.确定一些初始状态(边界状态)的值
以“数字三角形”为例,初始状态就是底边数字,值就是底边数字值。
4. 确定状态转移方程
定义出什么是“状态”,以及在该“状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
数字三角形的状态转移方程:
能用动规解决的问题的特点
1) 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的,我们就称该问题具有最优子结 构性质。
2) 无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
在我的上一篇文章中已经详细讲解了动态规划的原理和如何使用动态规划解题。本篇文章,我将继续通过例子来让大家更加熟练地使用动态规划算法。
话不多说,来看如下例题,也是在动态规划里面遇到过的最频繁的一个题,本题依然来自于北大POJ:
最长公共子序列(POJ1458)
给出两个字符串,求出这样的一个最长的公共子序列的长度:子序列中的每个字符都能在两个原串中找到, 而且每个字符的先后顺序和原串中的先后顺序一致。
Sample Input
abcfbc abfcab
programming contest
abcd mnp
Sample Output
4
2
0
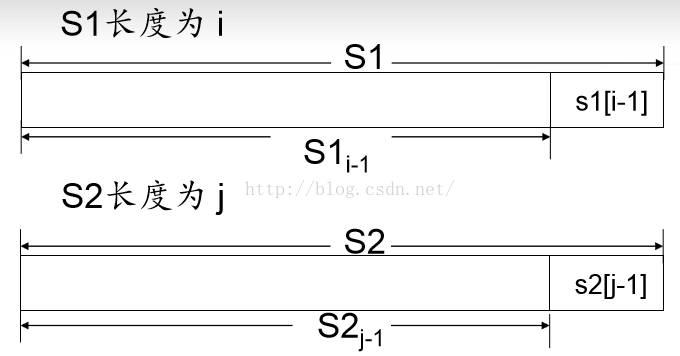
解题思路:设输入的两个串为s1,s2, 设MaxLen(i,j)表示::s1的左边i个字符形成的子串,与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0 开始算),则MaxLen(i,j) 就是本题的“状态” (如果还不懂“状态”是什么意思,可以参考我上一篇文章)
假定 len1 = strlen(s1),len2 = strlen(s2),那么题目就是要求 MaxLen(len1,len2)
显然:
MaxLen(n,0) = 0 ( n= 0…len1)
MaxLen(0,n) = 0 ( n=0…len2)
于是,我们可以得到如下的递推公式:
时间复杂度O(mn) m,n是两个字串长度
S1[i-1]!= s2[j-1]时,MaxLen(S1,S2)不会比MaxLen(S1,S2j-1) 和MaxLen(S1i-1,S2)两者之中任何一个小,也不会比两者都大。
通过上面的分析,我们很简单就可以写出如下的代码:
然后提交我们的代码,一次AC。
接下来我们再来看一道典型的例题:
最长上升子序列(百练2757)
一个数的序列ai,当a1 < a2 < ... < aS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, ..., aN),我们可以得到一些上升的子序列(ai1, ai2, ..., aiK),这里1 <= i1 < i2 < ... < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8), 有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8).。
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
输入数据
输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000。
输出要求
最长上升子序列的长度。
输入样例
7
1 7 3 5 9 4 8
输出样例
4
解题思路
1.找子问题
“求序列的前n个元素的最长上升子序列的长度”是个子问题,但这样分解子问题,不具有“无后效性”,因为假设F(n) = x,但可能有多个序列满足F(n) = x。有的序列的最后一个元素比 an+1小,则加上an+1就能形成更长上 升子序列;有的序列最后一个元素不比an+1小……以后的事情受如何达到状态n的影响,不符合“无后效性” ,因此我们必须换一种思路来解决此问题。
“求以ak(k=1, 2, 3…N)为终点的最长上升子序列的长度”,一个上升子序列中最右边的那个数,称为该子序列的 “终点”。虽然这个子问题和原问题形式上并不完全一样,但是只要这N个子问题都解决了,那么这N个子问题的解中, 最大的那个就是整个问题的解。
2.确定状态
子问题只和一个变量—— 数字的位置相关。因此序列中数的位置k就是“状态”,而状态 k 对应的“值”,就是以ak做为“终点”的最长上升子序列的长度。 状态一共有N个。
3.找出状态转移方程
maxLen (k)表示以ak做为“终点”的
最长上升子序列的长度那么:
初始状态:maxLen (1) = 1
maxLen (k) = max { maxLen (i):1<=i < k 且 ai < ak且 k≠1 } + 1 若找不到这样的i,则maxLen(k) = 1
maxLen(k)的值,就是在ak左边,“终点”数值小于ak ,且长度最大的那个上升子序列的长度再加1。因为ak左边任何“终点”小于ak的子序列,加上ak后就能形成一个更长的上升子序列。
有了这个思路,我们就可以很轻松地写出代码了。然而,即使到了这里,我们依然还能从两个方向解决这道题,我们可以将它们分别称为“人人为我”递推型动归和“我为人人”递推型动归 。请看下面的讲解:
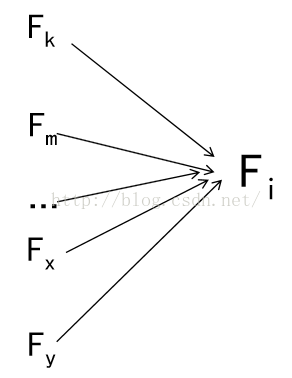
“人人为我”递推型动归
状态i的值Fi由若干个值 已知的状态值Fk,Fm,..Fy 推出,如求和,取最大值
根据这个方向,我们不难写出如下代码:
下面是我这段代码的提交结果:
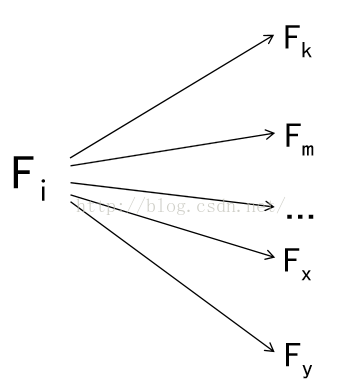
“我为人人”递推型动归
状态i的值Fi在被更新(不一定是 最终求出)的时候,依据Fi去更 新(不一定是最终求出)和状态i 相关的其他一些状态的值 Fk,Fm,..Fy
根据这个方向,我们又可以写出如下代码:
下面是我这段代码的提交结果:
接下来,就要进行一个总结了:
动规的三种形式
1)记忆递归型
优点:只经过有用的状态,没有浪费。递推型会查看一些 没用的状态,有浪费。
缺点:可能会因递归层数太深导致栈溢出,函数调用带来额外时间开销。总体来说,比递推型慢。
2) “我为人人”递推型
没有什么明显的优势,有时比较符合思考的习惯。个别特殊题目中会比“人人为我”型节省空间。
3)“人人为我”递推型
在选取最优备选状态的值Fm,Fn,…Fy时, 有可能有好的算法或数据结构可以用来显 著降低时间复杂度。



















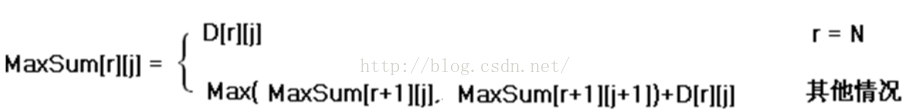
















 2291
2291











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








