关于高维超正体（cross-polytope）的性质及其应用

关于高维空间，有一个非常反直觉的事实，但是却很重要，特别是对于理解压缩感知理论以及LASSO都是及其重要的！

首先，我们从低维空间的一个很直观的事实说起——任何一条直线（二维空间）或者平面（三维空间）都必定会与坐标轴相交。但是一个平面会不会在四维空间中与坐标轴相交呢？答案是否定的，这就相当于你把直线放到三维空间中一样，这条直线不一定会和坐标轴相交。所以，一般对于一个N维空间而言，只有维度为(N-1)的子空间才有可能和坐标轴相交。

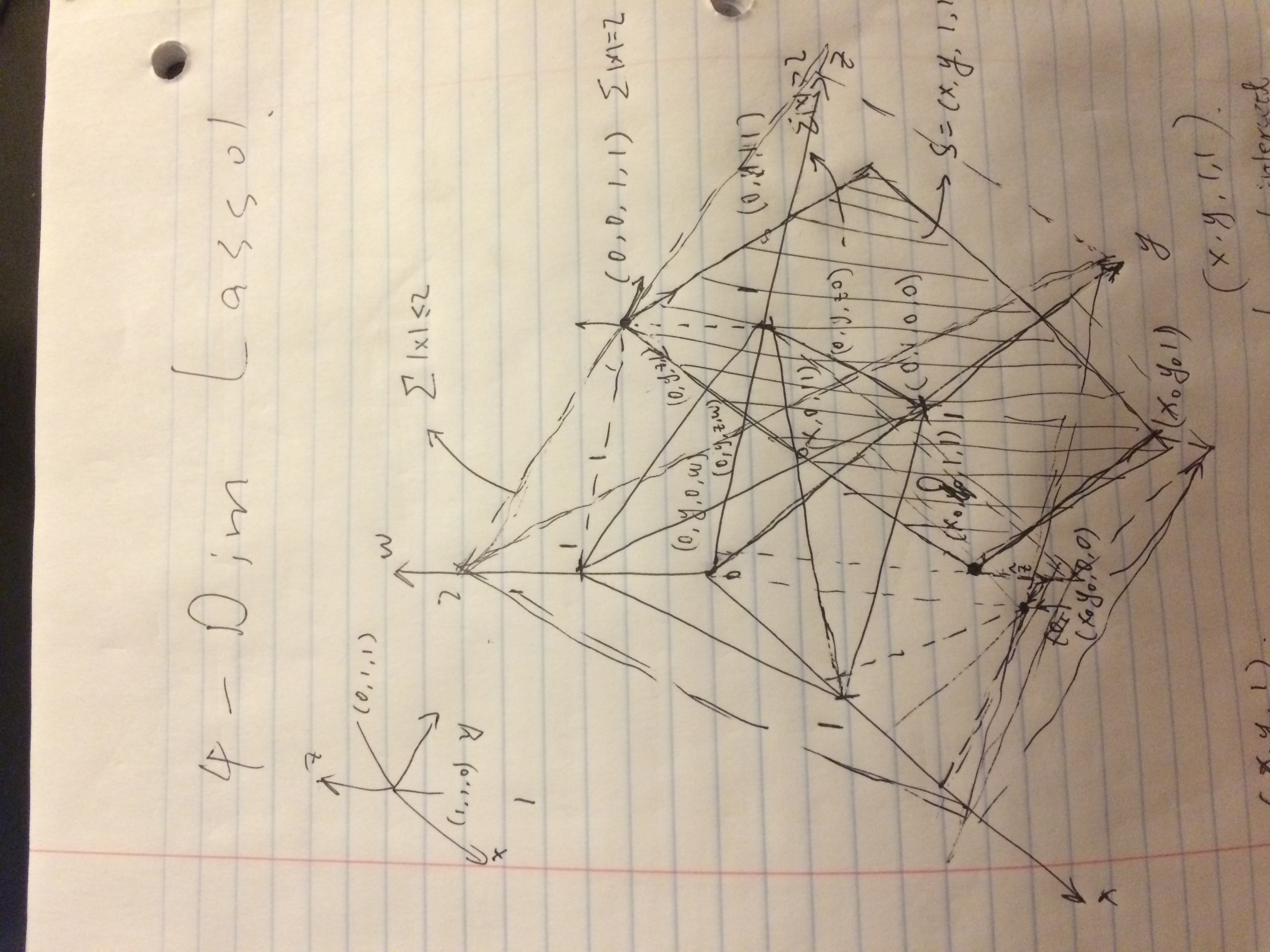
那么，一个高维超正体（cross-polytope）又有什么性质呢？毕竟，这个是压缩感知理论以及LASSO的核心：

观察后发现一个很重要的属性，那就是超正体的棱和坐标轴总是会围成一个三维的正四面胞体，每个胞体都是独立存在的，超正体就是由所有各个维度组合小的胞体共同构成的。这样，当超正体开始生长时，其实是在每个正交的三维子空间中独立的扩展胞体。假设我们在超正体外面一定距离内套一个超球面，那么随着超正体的生长，我们可以清晰的看到是哪一部分先抵达超球面，哪一部分后抵达。所以最先抵达的一定是顶点，其次是棱，而后是棱和坐标轴构成的二维平面，然后是单个的胞体构成的三维空间，然后是两个胞体的坐标轴组合构成的四维空间，然后是三个胞体的坐标轴组合构成的五维空间，依此类推。。。所以，最后通过的是超正体的中心部分，那是一个N维空间，N是超正体所处空间的维度。

超正体的这一性质非常好，为什么？因为它允许我们在由低到高的维度层面上一级级的筛选所需要的信息。所以，当我们做优化时，假如用了LASSO，那么实际上我们是在试图用一个高维的目标函数去侵入超正体，由于侵入区域的维度增长是由低到高的，所以首先出现的交点必定是维度最低的，最后的结果就是找到一个维度最低且最靠近最优解的解，这就是为什么LASSO可以用来做feature selection。

在压缩感知理论中，同样使用了L1范数优化，其目的是模拟L0优化从而获取稀疏解。为什么L1可以用来模拟L0？因为二者的本质实际上都是尽可能的降低维度的，在可行解空间中那个维度最低的解就是我们要求的稀疏解。但是与LASSO不同的是，我们并不是用一个对象去侵入一个已知的超正体，相反，我们从原点开始生长一个高维超正体，然后找首先碰到可行解空间的那个交点。

所以对于这个生长过程，一个重要的事实是：在高维空间中，解空间很难与预期高维超正体的内部相交，这点很重要，因为你可以想象一下如果超正体在生长的过程中首先接触到解空间的部分的维度如果高于预期的维度会怎么样？这时候L0就不再和L1等价了！这种情况是有可能的，为了简化思想，你可以把超正体想象成一个正八面体，然后解空间是一条直线，那么这条直线可以和坐标轴相交的同时还穿过预期的超正体，这就意味着超正体的生长并不能达到预期程度，可能在一个棱接触到直线的时候就停止了，这时候的交点就必定是处于一个二维平面中的，而非预期的坐标轴上。那么为什么在高维空间中我们不用担心因为解空间穿过预期超正体而导致交点出现在比预期更高维的空间中？因为维度诅咒（这里其实是祝福了^_^）:

高维空间中，超正体的大部分“体积”都集中在坐标轴附近，因为你可以想象它的每一个顶点对应的“底面积”都非常非常的小（V(n)=2^n/n!），这就导致它看上去很尖很尖，你完全可以想象高维超正体就是一个“海胆”，但是身子特别小，然后在各个坐标轴上都布满了等长的刺。所以，你要穿过预期超正体就意味着你得几乎和坐标轴相交，你可以想象在三维空间中一条任意的直线和坐标轴相交的概率是相当小的（即那个反直觉的事实）。所以，无论如何，出现因为解空间穿过预期超正体而导致交点出现在比预期更高维的空间中的概率几乎是0，而且空间维度越高，这种可能性就越小。。。