1、主成分分析(PCA)介绍
主成分分析(Principal Component Analysis,PCA),是一种统计方法。
在处理实际问题中,多个变量之间可能存在一定的相关性,当变量的个数较多且变量之间存在复杂的关系时,增加了问题分析的难度。
主成分分析是一种数学降维的方法,该方法主要将原来众多具有一定相关性的变量,重新组合成为一种新的相互无关的综合变量。
例如,当选择第一个线性组合即第一个综合变量为F1,希望F1能够反映更多的信息,因此F1在所有线性组合中的方差是最大的,此时F1为第一主成分。如果F1作为第一主成分,不足以代表原来P个变量的信息,则继续选择F2作为第二个线性组合,为了更加有效的反映最初的信息,F1已经具有的信息不需要再次反映在F2中,那么要求此时Cov(F1,F2)=0,则F2可以称之为第二主成分。以此类推,可以构造出多个主成分。
2、主成分分析的主要步骤
(1)对原始数据进行标准化处理
若样本数据矩阵如下:
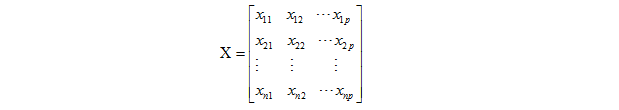
对原始数据进行标准化处理:
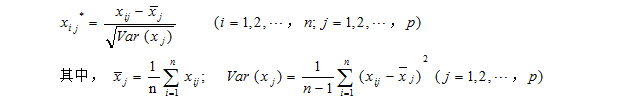
matlab代码如下:
%数据的标准化处理:由矩阵A得到标准化后的矩阵SA
a=size(A,1);
b=size(A,2);
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));
end
(2)计算样本相关系数矩阵
(注意这里假设原始数据标准化后仍用X表示,后面给出的计算该系数矩阵元素值的方法中设计到的Xi和Xj并不是原始数据矩阵X,而是标准化后的矩阵元素,这是这里依旧用了X表示而已!)
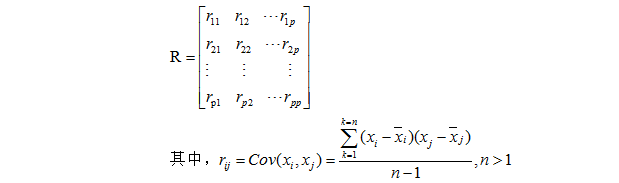
matlab代码:
%计算系数矩阵:CM
CM=corrcoef(SA);
(3)计算相关系数矩阵R的特征值和相应的特征向量:
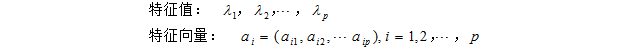
%计算CM的特征值和特征向量
[V,D]=eig(CM);
(4)选择重要的主成分:
由主成分分析可以得到P个主成分,根据前面的介绍,主成分F1包含的信息大于F2,且可以以此类推,因此各个主成分的方差也是递减的,包含的信息量也是递减的,所以实际使用该方法的时候不在选取所有的P个主成分,而是根据各个主成分累计贡献的大小选取前面K个主成分。这里的贡献率是指某个主成分的方差占据全部主成分方差的比重,也就是某个特征值占据全部特征值和的比重,即:
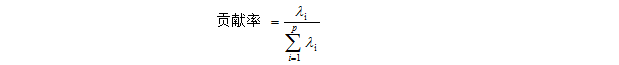
%将特征值按降序排列到DS中
for j=1:b
DS(j,1)=D(b+1-j,b+1-j);
end
%计算贡献率
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));%单个贡献率
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率
end
某个主成分的贡献率越大说明该主成分包含的原始信息量越大,主成分K值的选取,主要依据主成分 累计贡献率来决定,一般来说当累计贡献率达到85%以上时,可以认为这K个主成分包含了原始信息绝大多数的信息。
(5)计算主成分得分
其形式如下:
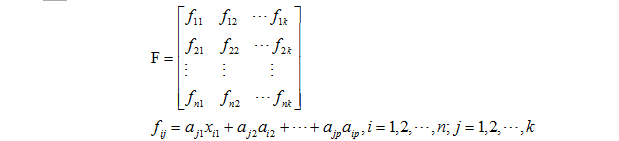
%假定主成分的信息保留率
T=0.9;
for k=1:b
if DS(k,3) >= T
com_num=k;
break;
end
end
%提取主成分的特征向量
for j=1:com_num
PV(:,j)=V(:,b+1-j);
end
%计算主成分得分
new_score=SA*PV;
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
%强主成分得分与总分放到同一个矩阵中
result_report=[new_score,total_score];
%按总分降序排列
result_report=sortrows(result_report,-4);
%输出结果
disp('特征值、贡献率、累计贡献率:')
DS
disp('信息保留率T对应的主成分数与特征向量:')
com_num
PV
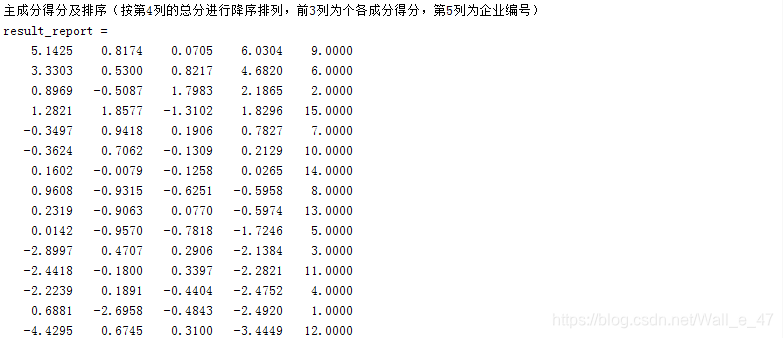
disp('主成分得分及排序(按第4列的总分进行降序排列,前3列为个各成分得分,第5列为企业编号)')
result_report
(6)根据主成分得分的数据对问题进行后续的分析和建模。
案例
数据:对15家企业通过8个不同指标数据进行评估。
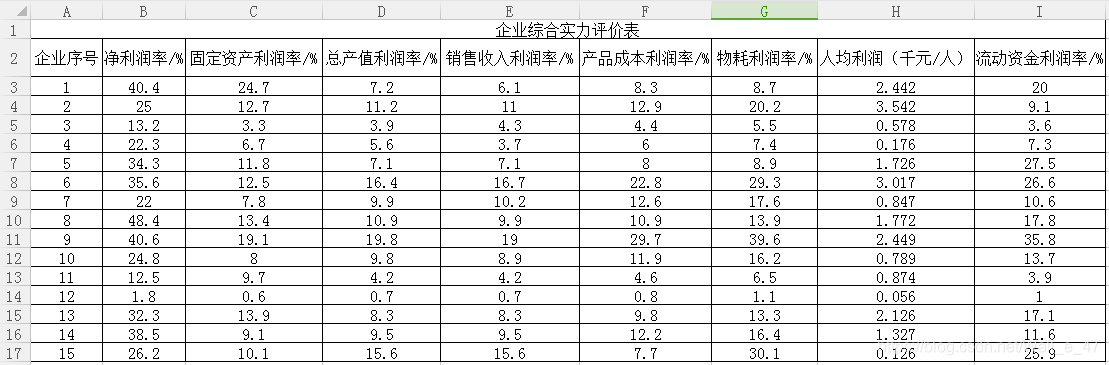
Matlab代码:
clc
clear all
A=xlsread('D:\资料库区\大三上\HUAWEI\MATLAB\主成分分析.xls','B3:I17');
%得到的数据矩阵的行数和列数
a=size(A,1);
b=size(A,2);
%数据的标准化处理:得到标准化后的矩阵SA
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));
end
%计算系数矩阵:CM
CM=corrcoef(SA);
%计算CM的特征值和特征向量
[V,D]=eig(CM);
%将特征值按降序排列到DS中
for j=1:b
DS(j,1)=D(b+1-j,b+1-j);
end
%计算贡献率
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));%单个贡献率
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率
end
%假定主成分的信息保留率
T=0.9;
for k=1:b
if DS(k,3) >= T
com_num=k;
break;
end
end
%提取主成分的特征向量
for j=1:com_num
PV(:,j)=V(:,b+1-j);
end
%计算主成分得分
new_score=SA*PV;
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
%强主成分得分与总分放到同一个矩阵中
result_report=[new_score,total_score];
%按总分降序排列
result_report=sortrows(result_report,-4);
%输出结果
disp('特征值、贡献率、累计贡献率:')
DS
disp('信息保留率T对应的主成分数与特征向量:')
com_num
PV
disp('主成分得分及排序(按第4列的总分进行降序排列,前3列为个各成分得分,第5列为企业编号)')
result_report
Matlab运行结果:























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








