考研数学 之 汤家凤老师来校讲座摘记 (拉格朗日定理等干货 )
2021年3月12日
刚开始复习考研数学没多久
得知大名鼎鼎的汤神要来我们学校做讲座
在某帅气的zqq推荐下 我参与了这次讲座
听完讲座之后感觉受益匪浅
于是打算写这篇文章来记录一下
摘要
先放几张讲座现场的照片
正文
主要还是记录一下这次讲座的一些收货和我觉得学习到的干货
学习规划
学习的规划方面主要有以下三点
- 在6.30日前完成基础阶段的复习
- 基础课的学习要系统
- 可以看汤老师在B站的视频, (虽然我买了其他老师的课,但汤老师的讲课水平是不容置疑的)
- 我觉得一旦选定了基础课的老师就不要换了,每个老师都有自己讲课的风格和安排,随意更换可能会产生一些问题
- 练习
- 这一点非常重要, 数学的学习需要大量的练习,每章学习完之后都要进行大量的题目练习,不然很容易忘记
方法体系有如下两点
- 理论体系
- 方法体系
干货记录
在讲座中, 汤老师带来的大多数都是干货, 我就选取其中重要的部分做一个简单的记录
定积分
现在网上大多数讲解定积分都是从下面这张图来展开的
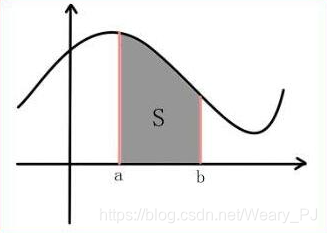
但是当我们看到这张图的时候,我们要想到的更多
- A = ? A = ? A=? (阴影部分的面积)
- V x = ? V_x = ? Vx=? (曲线绕 x 轴旋转的面积)
- V y = ? V_y = ? Vy=? (曲线绕 y 轴旋转的面积)
- $S = ? $ (绕X轴旋转体的侧面积)
拉格朗日定理
接下来的一大段时间,汤神都在介绍拉格朗日定理
对拉格朗日的一套体系让我受益匪浅
之前只是停留在会做题的阶段 而没有形成一套体系
下面就记录一下汤神对拉格朗日的总结
定理介绍
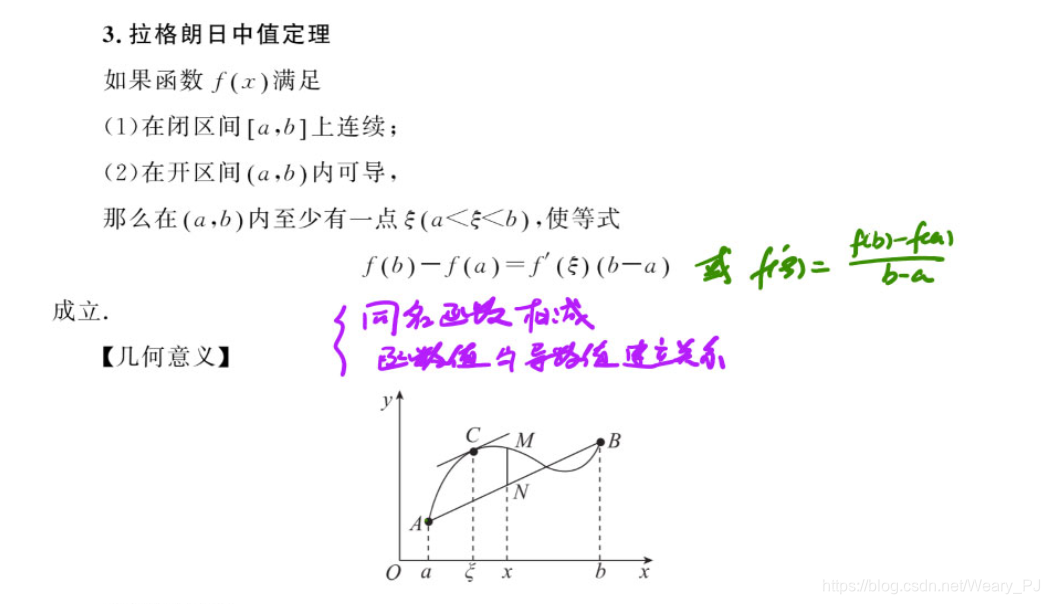
通常若题目中出现如下几种情况时 要使用拉格朗日定理
- f ( b ) − f ( a ) f(b) - f(a) f(b)−f(a) 90 % 90\% 90%的几率要用
- f ( a ) ≠ f ( b ) f(a) ≠ f(b) f(a)=f(b) 可能用 可能不用
- f ( a ) , f ( b ) , f ( c ) f(a) ,f(b),f(c) f(a),f(b),f(c) 使用两次定理
- 从 f ( x ) f(x) f(x) 指向 f ′ ( x ) f'(x) f′(x)
接下来便是一些案例来帮助我们理解, 下面是我记录的部分题目
案例2
已知 f ′ ′ > 0 , 求 f ′ ( 0 ) , f ′ ( 1 ) . f ( 1 ) − f ( 0 ) 三 者 之 间 的 大 小 f''>0, 求 f'(0), f'(1). f(1)-f(0) 三者之间的大小 f′′>0,求f′(0),f′(1).f(1)−f(0)三者之间的大小
解析
本题出现了
f
(
1
)
−
f
(
0
)
f(1)-f(0)
f(1)−f(0) 也就是
f
(
b
)
−
f
(
a
)
f(b) - f(a)
f(b)−f(a)的形式
很自然的想到用拉格朗日定理
f
(
1
)
−
f
(
0
)
=
f
′
(
ξ
)
(
1
−
0
)
ξ
∈
(
0
,
1
)
f(1)-f(0)=f'(\xi)(1-0) \ \ \ \ \ \ \xi\in(0,1)
f(1)−f(0)=f′(ξ)(1−0) ξ∈(0,1)
∵
f
′
′
>
0
∵ f''>0
∵f′′>0$
∴
f
′
在
(
0
,
1
)
上
单
调
递
增
∴f'在(0,1)上单调递增
∴f′在(0,1)上单调递增
∴
f
′
(
0
)
<
f
′
(
ξ
)
<
f
′
(
1
)
∴f'(0)<f'(\xi)<f'(1)
∴f′(0)<f′(ξ)<f′(1)
案例2
lim
x
→
+
∞
x
2
(
s
i
n
1
x
−
s
i
n
1
x
+
1
)
\lim\limits_{x\rightarrow+\infty}x^2(sin\frac{1}{x}- sin\frac{1}{x+1})
x→+∞limx2(sinx1−sinx+11)
解析
f
(
t
)
=
s
i
n
x
f(t) = sinx
f(t)=sinx
然后用拉格朗日
案例3
已知
f
′
′
>
0
f''>0
f′′>0 求证
2
f
(
1
)
<
f
(
0
)
+
f
(
2
)
2f(1) < f(0) + f(2)
2f(1)<f(0)+f(2)
解析
拆成如下
f
(
1
)
−
f
(
0
)
<
f
(
2
)
−
f
(
1
)
f(1) - f(0) < f(2) - f(1)
f(1)−f(0)<f(2)−f(1)
两次拉格朗日
f ( n ) ( ξ ) = 0 f^{(n)}(\xi)=0 f(n)(ξ)=0形式的解法
f
(
n
)
(
ξ
)
=
0
f^{(n)}(\xi)=0
f(n)(ξ)=0
n
=
1
时
:
{
找
f
(
a
)
=
f
(
b
)
用
罗
尔
定
理
极
值
点
☆
(
一
般
书
上
不
讲
这
个
方
法
)
n = 1时: \begin{cases} 找 f(a)=f(b) 用罗尔定理 \\ 极值点 \ \ \ \ ☆(一般书上不讲这个方法) \end{cases}
n=1时:{找f(a)=f(b)用罗尔定理极值点 ☆(一般书上不讲这个方法)
n
=
2
时
:
{
找
f
(
a
)
=
f
(
b
)
=
f
(
c
)
找
f
′
(
a
)
=
f
′
(
b
)
n = 2时: \begin{cases} 找 f(a)=f(b)=f(c)\\ 找 f'(a) = f'(b) \end{cases}
n=2时:{找f(a)=f(b)=f(c)找f′(a)=f′(b)
案例
f
(
0
)
=
1
,
f
(
1
2
)
=
2
,
f
(
1
)
=
−
1
,
证
∃
ξ
∈
(
0
,
1
)
f
′
(
ξ
)
=
0
f(0)=1, f(\frac{1}{2})=2, f(1)=-1, 证\exists\xi\in(0,1) \ \ \ \ f'(\xi)=0
f(0)=1,f(21)=2,f(1)=−1,证∃ξ∈(0,1) f′(ξ)=0
解析
令
ϕ
(
x
)
=
f
(
x
)
−
1
\phi(x) = f(x)-1
ϕ(x)=f(x)−1
然后通过零点定理找出
ϕ
(
c
)
=
0
=
ϕ
(
0
)
\phi(c) = 0 = \phi(0)
ϕ(c)=0=ϕ(0)
结束
先记录这么多吧
附上汤老师的签名, 祝大家考研数学路上顺利
1037
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
