介绍:在频域上进行滤波操作,增强高频信息以恢复清晰图像。
优点:在频域上操作相对的高效,能够快速处理大尺寸的图像。
缺点:需要适当调度滤波器设计,需要调整参数来获得最佳效果。
深度学习方法与频域处理方法的差异:
- 深度学习方法
- 定义:深度学习是一种基于人工神经网络的机器学习方法,它可以对大量的数据进行自动化的特征提取和模式识别,以实现复杂的任务。
- 基本原理:深度学习模型通过多层非线性处理单元(神经元)的堆叠,逐层抽象数据特征,从低级的边缘、纹理等特征到高级的语义特征,最终实现分类、回归或生成等任务。
2.频域处理方法
- 定义:频域处理是一种将信号或图像从时间域(或空间域)转换到频率域进行分析和处理的技术。
- 基本原理:通过傅里叶变换(如离散傅里叶变换DFT、快速傅里叶变换FFT)将信号或图像分解为不同频率的分量,然后在频域上进行滤波、增强、复原等操作,最后通过逆变换回到时间域(或空间域)。
应用领域:
- 深度学习方法
- 应用领域:广泛应用于图像识别、自然语言处理、语音识别、推荐系统等领域。
- 特点:
- 自动化特征提取:能够自动从原始数据中提取出有用的特征,减少了对人工特征工程的依赖。
- 非线性建模能力:通过多层非线性处理单元,能够捕捉数据中的复杂非线性关系。
- 端到端学习:可以实现从输入到输出的直接映射,简化了模型的设计和训练过程。
- 频域处理方法
- 应用领域:主要用于图像处理、信号处理等领域。
- 特点:
- 频域分析:能够在频域上直观地分析信号的频率成分,便于进行滤波、去噪等操作。
- 高效计算:利用FFT等算法,可以高效地计算信号的傅里叶变换和逆变换。
- 灵活性强:可以通过设计不同的滤波器来实现不同的处理效果,如低通滤波、高通滤波等。
处理流程:
- 处理流程
- 深度学习方法:数据预处理 → 构建深度学习模型 → 模型训练 → 模型评估 → 预测或应用。
- 频域处理方法:信号或图像采集 → 傅里叶变换 → 频域处理(如滤波、增强等)→ 逆变换 → 处理结果输出。
- 差异
- 数据处理方式:深度学习方法直接在原始数据上进行特征提取和处理,而频域处理方法则先将数据转换到频域上进行处理。
- 模型复杂度:深度学习模型通常包含大量的参数和复杂的网络结构,而频域处理方法则相对简单,主要依赖于傅里叶变换和滤波器等工具。
- 适用范围:深度学习方法适用于大规模、复杂的数据处理任务,而频域处理方法则更适用于需要分析信号频率成分的场景。
深度学习方法和频域处理方法各有其独特的优势和适用场景。深度学习方法通过自动化特征提取和强大的非线性建模能力,在处理复杂、大规模的数据时表现出色;而频域处理方法则通过频域分析和高效的计算工具,在信号处理、图像处理等领域具有不可替代的作用。在实际应用中,可以根据具体任务的需求和数据特点选择合适的方法或结合使用这两种方法以达到更好的效果。
名词解释:
频域:频域是频率信号与该频率信号的幅度的关系。
频率:可以看作图像灰度的变化的幅度。(如果频率越大,则灰度变化幅度就很大,与相邻灰度值差别越大)
频谱中心:‘通常是指信号频率分布中的峰值位置,在傅里叶变换中他是反映信号主要成分的频率的关键信息。
如何将图像转化为频域振幅图像?
(一般的图像都是空间域图像,不能对频率进行操作)
1.傅里叶变换
- 使用傅里叶变换可以将图像的灰度值转化为频率
在matlab中可以使用fft2()函数计算二维快速傅里叶变换,所以读取的图像必须是二维灰度图像。如果不是就需要进行灰度变换
imag = imread("C:\Users\Pictures\练习图片\桥.jpg");//读取图像
imag_gray = rgb2gray(imag);//转换为灰度图像
subplot(1, 2, 1); imshow(imag_gray); title('原图像')//显示原始灰度图像
fu = fft2(imag_gray);//对灰度图像进行二维傅里叶变换
subplot(1, 2, 2); imshow(log(abs(fu)), [ ]); title('傅里叶变换后图像')
//显示傅里叶变换后的图像

!!!注意:上述代码显示频域图像的时候,关心的只有频率的**振幅,**频率有正有负,所以我们取其绝对值
频率非常大 非常小的情况下:解决办法:将频率值取对数,将其取值范围降低到一个很小的范围。
使用fftshift()函数将频谱中心转移到图像的中心
imag = imread("C:\Users\林梓烯\Pictures\练习图片\桥.jpg");
imag_gray = rgb2gray(imag);//转换为灰度图像
subplot(1, 2, 1); imshow(imag_gray); title('原图像')//显示原始灰度图像
fu = fftshift(fft2(imag_gray));//对灰度图像进行二位傅里叶变换,并且将结果中心化
subplot(1, 2, 2); imshow(log(abs(fu)), [ ]); title('傅里叶变换后图像')////显示傅里叶
变换后的图像。
转换后的图像:

我们在处理完频域图像之后,就需要将频率图像转换为灰度图像
可以使用傅里叶反变换
2.傅里叶反变换:
在进行反变换前,我们又需要将图像的频谱中心移回左上角,不然跟原图像完全不同。
在matlab我们使用ifft2函数来实现傅里叶反变换。
mag = imread("C:\Users\林梓烯\Pictures\练习图片\桥.jpg");
mag_gray = rgb2gray(imag);
ubplot(1, 3, 1); imshow(imag_gray); title('原图像')
u = fftshift(fft2(imag_gray));
ubplot(1, 3, 2); imshow(log(abs(fu)), [ ]); title('傅里叶变换后图像')
mag_x = ifft2(ifftshift(fu));
ubplot(1, 3, 3); imshow(imag_x, []); title('傅里叶反变换图像')
变换后的图像

以下是我自己在Matlab中复现的图片。
原图片->频域图像
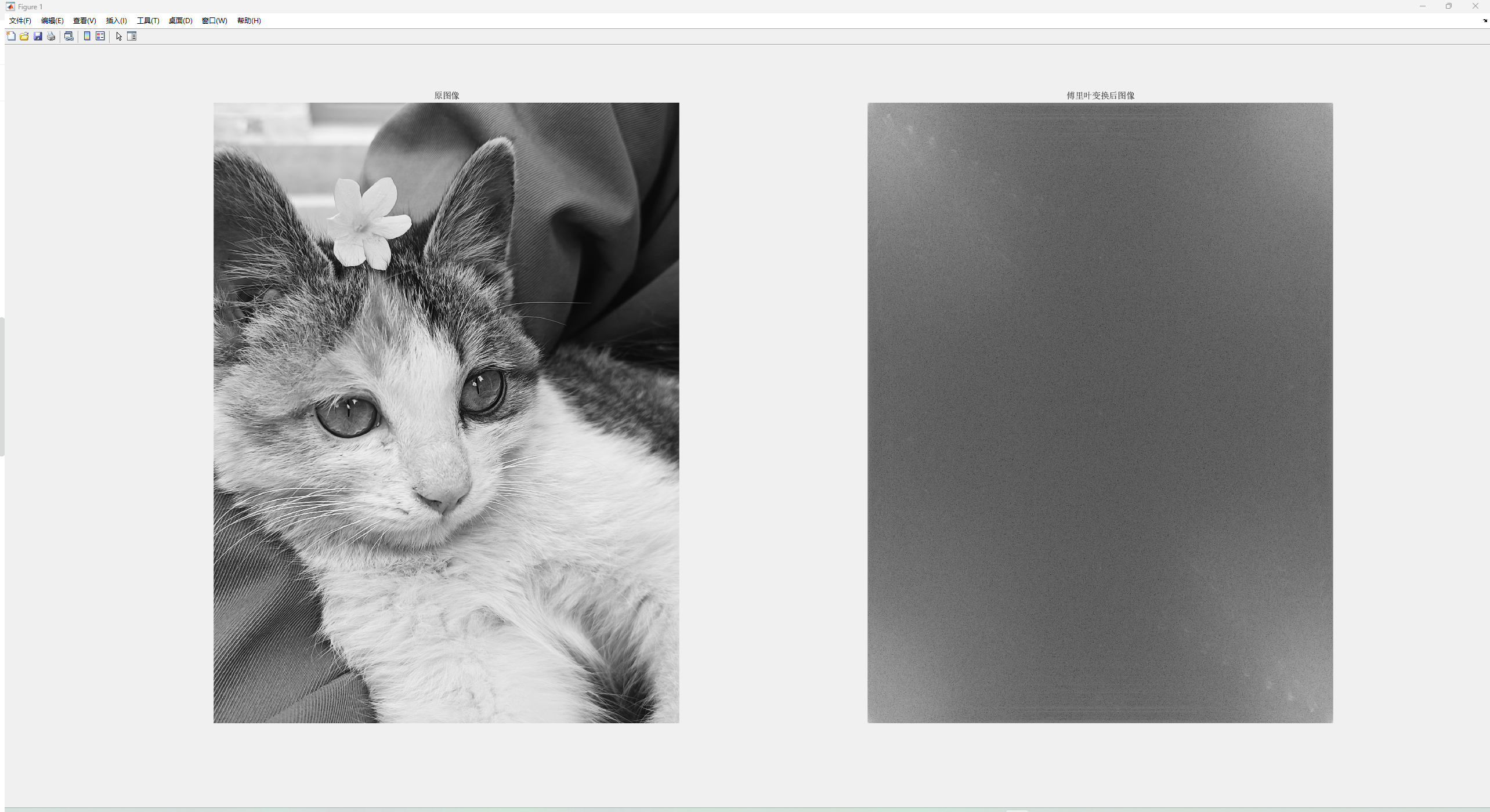
频域图像———>修改后的图像
实现代码如下:
% 读取图像
mag = imread("C:\Users\14331\Desktop\CatDemoPIN.png");
% 将图像转换为灰度图
mag_gray = rgb2gray(mag);
% 显示原图像
subplot(1, 3, 1);
imshow(mag_gray);
title('原图像');
% 对灰度图进行二维傅里叶变换,并中心化
u = fftshift(fft2(mag_gray));
% 显示傅里叶变换后的图像(通常使用对数尺度以便于观察)
f_u = u; % 确保变量名一致
subplot(1, 3, 2);
imshow(log(abs(f_u)), []);
title('傅里叶变换后图像');
% 进行傅里叶反变换并取消中心化
mag_x = ifft2(ifftshift(f_u));
% 显示傅里叶反变换后的图像
subplot(1, 3, 3);
imshow(mag_x, []);
title('傅里叶反变换图像');
% 注意:由于数值精度和可能的浮点运算误差,反变换后的图像可能与原图不完全相同

3.低通滤波器
是一种信号处理的滤波工具,用于从输入信号中去除高频部分,只保留高频部分
只允许通过低于截止频率调度信号,而减弱或消除高于截止频率的信号
为什么使用低频滤波器?
因为噪声和细节通常频率较高,因此使用低通滤波器能够去除噪声和消除一些细节。在数字图像处理中,低通滤波器可用于平滑图像,减少噪声,以改善图像质量。
实现机制:将高频信号舍弃(通低频,阻高频)
低通滤波器的类型:
(1)理想低通滤波器(Ideal Lowpass Filter):理想低通滤波器的频率响应是在截止频率之前完全允许所有低频信号通过,而在截止频率之后完全阻止所有高频信号。它在理论上是最简单的低通滤波器,但在实际应用中不常见,因为它需要无限的频带宽度,并且无法通过现实的电路来实现。
(2)巴特沃斯滤波器(Butterworth Filter):巴特沃斯滤波器是一种常见的低通滤波器,具有光滑的频率响应曲线,没有急剧的衰减或媒介。它通过一定的阶数来控制滤波器的频率特性。它的目标是在截止频率附近提供均匀的响应,以尽量保留信号的幅度。
(3)切比雪夫滤波器(Chebyshev Filter):切比雪夫滤波器也是一种常见的低通滤波器,它允许更多的波动或纹波在截止频率附近,以换取更陡峭的频率特性。它通常用于需要更高的阻抗匹配或更快的信号截断的应用。
如何运用低通滤波器?
步骤1: 提取低通滤波器的系数矩阵。
设计低通滤波器:
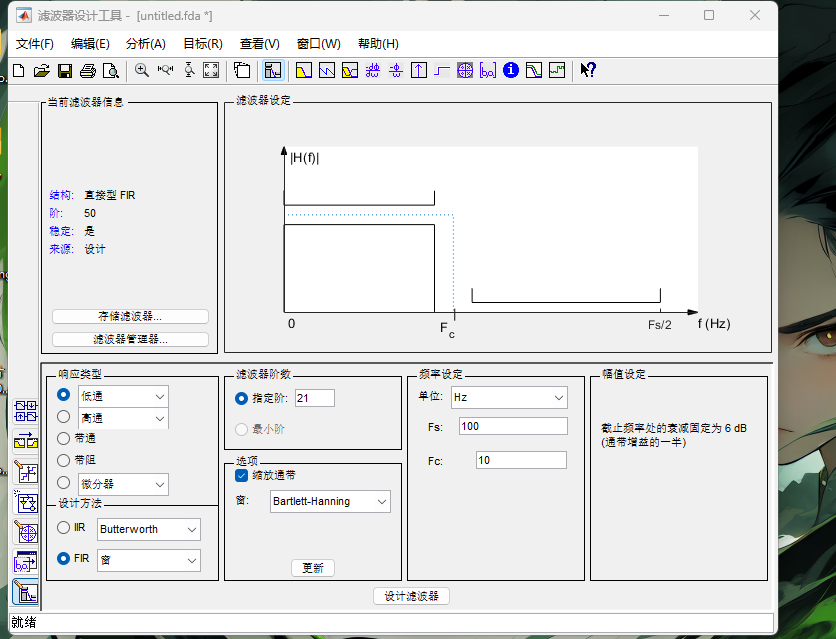
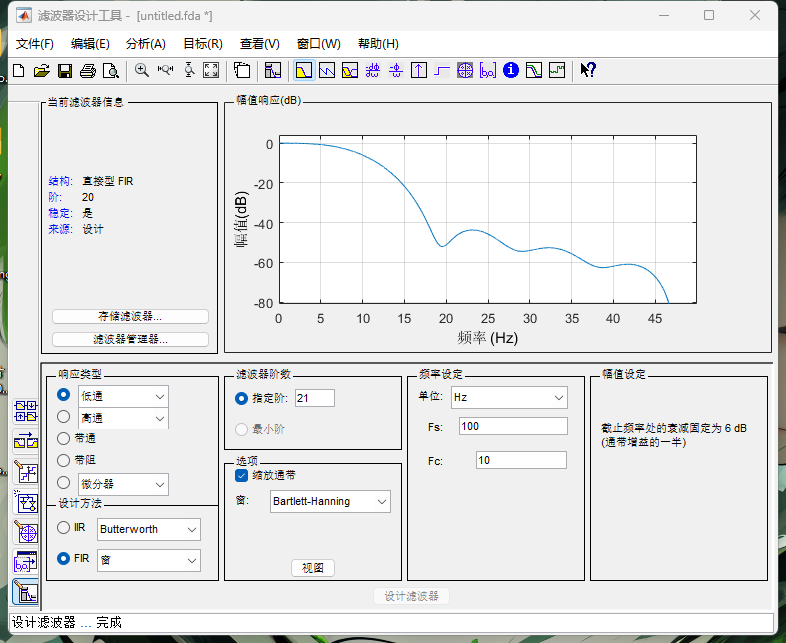
采用低通滤波器对信号进行滤波处理
% 清除工作空间变量、关闭所有图形窗口并清屏
clc;clear;close all;
% (1)获取数据
% 生成一个包含500个正态分布随机数的1x500数组作为原始信号
raw_signal = randn(1, 500);
% 计算原始信号的长度
raw_signal_len = length(raw_signal);
% (2)低通滤波器(Fs = 100Hz; Fc = 10Hz)
% 假设的滤波器系数,用于低通滤波,这些系数通常根据滤波器设计(如巴特沃斯、切比雪夫等)得到
% 系数矩阵对折对称,意味着滤波器是线性相位FIR滤波器
filter = [0, -0.0014, -0.0056, -0.0100, -0.0070, ...
0.0119, 0.0511, 0.1052, 0.1597, 0.1961, ...
0.1961, 0.1597, 0.1052, 0.0511, 0.0119, ...
-0.0070, -0.0100, -0.0056, -0.0014, 0];
% 计算低通滤波器的长度
filter_len = length(filter);
% 初始化滤波后的信号数组,开始时添加两个0,因为滤波操作会导致信号长度减少
filtered_signal = [0, 0];
% 应用低通滤波器
% 注意:由于滤波器的长度,滤波后的信号长度会减少
for ii = 1:raw_signal_len - filter_len + 1
sum_signal = 0;
% 对每个样本点应用滤波器
for jj = 1:filter_len
% 注意:这里使用(filter_len + 1) - jj是为了反转滤波器系数以匹配信号的读取顺序
sum_signal = sum_signal + raw_signal(ii + jj - 1) * filter((filter_len + 1) - jj);
end
% 存储滤波后的结果
filtered_signal(ii) = sum_signal;
end
% (3)画图
% 在第一个子图中绘制原始信号
subplot(2, 1, 1);
plot(1:raw_signal_len, raw_signal, 'Color', 'b');
title('原始曲线');
% 在第二个子图中绘制滤波后的信号
% 注意:由于滤波操作,滤波后信号的长度减少,因此索引范围为1:raw_signal_len - filter_len + 1
subplot(2, 1, 2);
plot(1:raw_signal_len - filter_len + 1, filtered_signal, 'Color', 'r');
title('滤波曲线');
演示结果:
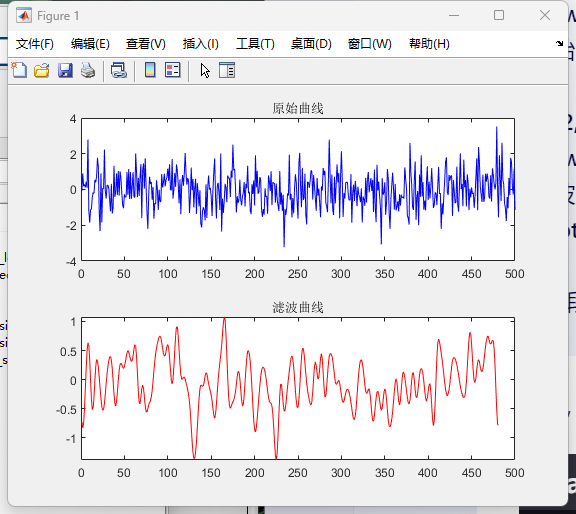
低通滤波器->图像处理
close all; clear all; clc;
% 读取图像并转换为双精度浮点数
I = imread('D:\resource_photo\3.png');
I = im2double(I);
% 获取图像尺寸
[rows, cols, ~] = size(I);
% 滤波器尺寸设置为图像尺寸的两倍(但通常不需要这么大,这里仅为示例)
M = 2 * rows;
N = 2 * cols;
% 创建频率坐标网格
u = -M/2:(M/2-1);
v = -N/2:(N/2-1); % 注意这里应该是 N/2 而不是 M/2
[U, V] = meshgrid(u, v);
% 计算距离原点的距离
D = sqrt(U.^2 + V.^2);
% 定义截止频率和滤波器阶数
D0 = 50; % 截止频率(注意这里的单位,通常与图像尺寸相关)
n = 6; % 滤波器的阶数
% 构建巴特沃斯低通滤波器
H = 1 ./ (1 + (D ./ D0).^(2 * n));
% 注意:这里不需要将H扩展到与I相同的尺寸,因为fft2会自动进行填充
% 但为了演示,我们可以这样做(通常不是必要的)
H = H(1:rows, 1:cols); % 如果H比I大,裁剪到I的尺寸
% 对图像进行二维FFT,并应用fftshift将零频率分量移到频谱中心
J = fftshift(fft2(I));
% 应用滤波器
K = J .* H;
% 逆傅里叶变换并再次应用ifftshift以恢复原始空间位置
L = ifft2(ifftshift(K));
% 由于进行了扩展的FFT,现在需要将结果裁剪回原始图像尺寸
L = real(L(1:rows, 1:cols)); % 取实部,因为对于实数输入,ifft2的输出应为实数
% 显示原图像和滤波后的图像
figure;
subplot(1, 2, 1); imshow(I); title('原图像');
subplot(1, 2, 2); imshow(L, []); title('经过巴特沃斯低通滤波后的图像');

close all; clear all; clc;
% 读取图像并转换为双精度浮点数
I = imread("C:\Users\14331\Desktop\微信图片_20240404190509.jpg");
if size(I, 3) == 3 % 如果是彩色图像,则转换为灰度图像
I = rgb2gray(I);
end
I = im2double(I);
% 获取图像尺寸
[rows, cols] = size(I);
% 计算滤波器尺寸(这里设置为图像尺寸的两倍,但通常不需要这么大)
M = 2 * rows;
N = 2 * cols;
% 创建频率坐标网格
u = -floor(M/2):(M/2-1); % 使用floor确保u是整数
v = -floor(N/2):(N/2-1); % 同样,v也是整数
[U, V] = meshgrid(u, v);
% 计算距离原点的距离
D = sqrt(U.^2 + V.^2);
% 定义截止频率
D0 = 60; % 注意这里的截止频率单位是“像素距离”,它可能需要根据图像大小进行调整
% 构建理想低通滤波器
H = double(D <= D0); % 滤波器在D<=D0时为1,否则为0
% 注意:由于H是二值的,且可能比I大,我们需要将其裁剪到与I相同的尺寸
H = H(1:rows, 1:cols);
% 对图像进行二维FFT,并应用fftshift将零频率分量移到频谱中心
J = fftshift(fft2(I)); % 注意:这里不需要指定fft2的输出大小,因为fft2会自动处理
% 应用滤波器
K = J .* H;
% 逆傅里叶变换并再次应用ifftshift以恢复原始空间位置
L = ifft2(ifftshift(K));
% 由于H已经裁剪到与I相同的尺寸,L现在也是正确的尺寸,但最好还是确认一下
L = real(L); % 取实部(尽管对于理想滤波器,这通常是多余的)
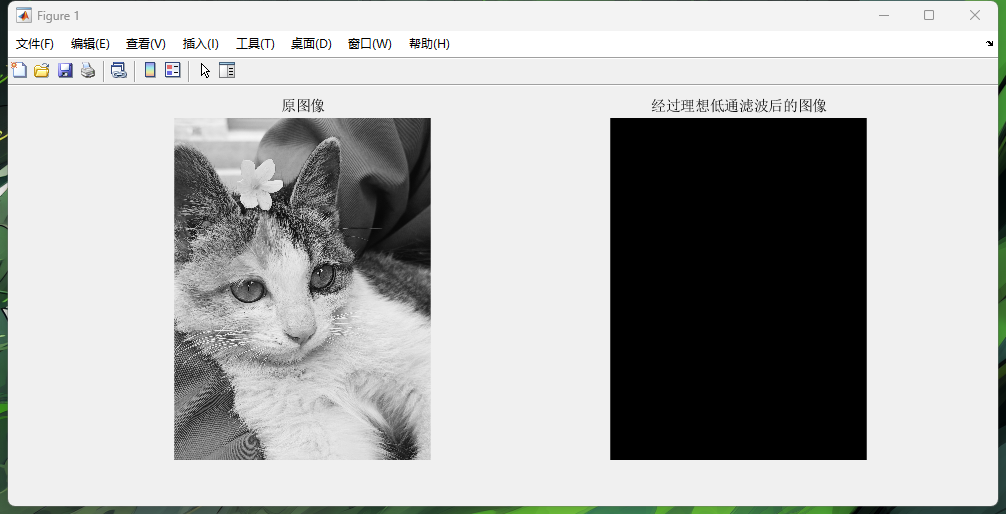
% 显示原图像和滤波后的图像
figure;
subplot(1, 2, 1); imshow(I); title('原图像');
subplot(1, 2, 2); imshow(L, []); title('经过理想低通滤波后的图像');
可能哪里调试错误了,我也不知道怎么回事
4.高通滤波器
为什么使用高通滤波器?
使用高通滤波可以突出显示图片的高频区域,如图片边缘部分和细节部分。。原理:通高频阻止低频
高斯滤波:
高斯滤波是图像处理中常用的一种滤波方式,它基于高斯分布的函数来设计滤波器,具有平滑图像的特性。
原理:(了解就行)
(1)高斯低通滤波(Gaussian Lowpass Filtering)
高斯低通滤波器通过对图像进行高斯模糊,滤除图像中的高频成分,从而实现图像的平滑。其频域中的传递函数为:
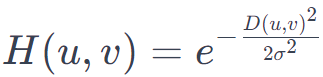
** 其中 D(u,v) 是频域中点(u,v) 到中心的距离,σ 是高斯分布的标准差。**
clear
clc
I = imread("C:\Users\14331\Desktop\微信图片_20240404190509.jpg"); % 读入图像
I = rgb2gray(I);
I=im2double(I);
M=2*size(I,1); %滤波器的行数
N=2*size(I,2); %滤波器的列数
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u, v);
D=sqrt(U.^2+V.^2);
sigma=20; %截止频率
H=exp(-(D.^2)./(2*(sigma^2))); %设计高斯滤波器
J=fftshift(fft2(I, size(H, 1), size(H, 2))); %空域转换到频域
K=J.*H; %滤波处理
L=ifft2(ifftshift(K)); %傅里叶反变换
L=L(1:size(I,1), 1:size(I, 2)); %改变图像大小
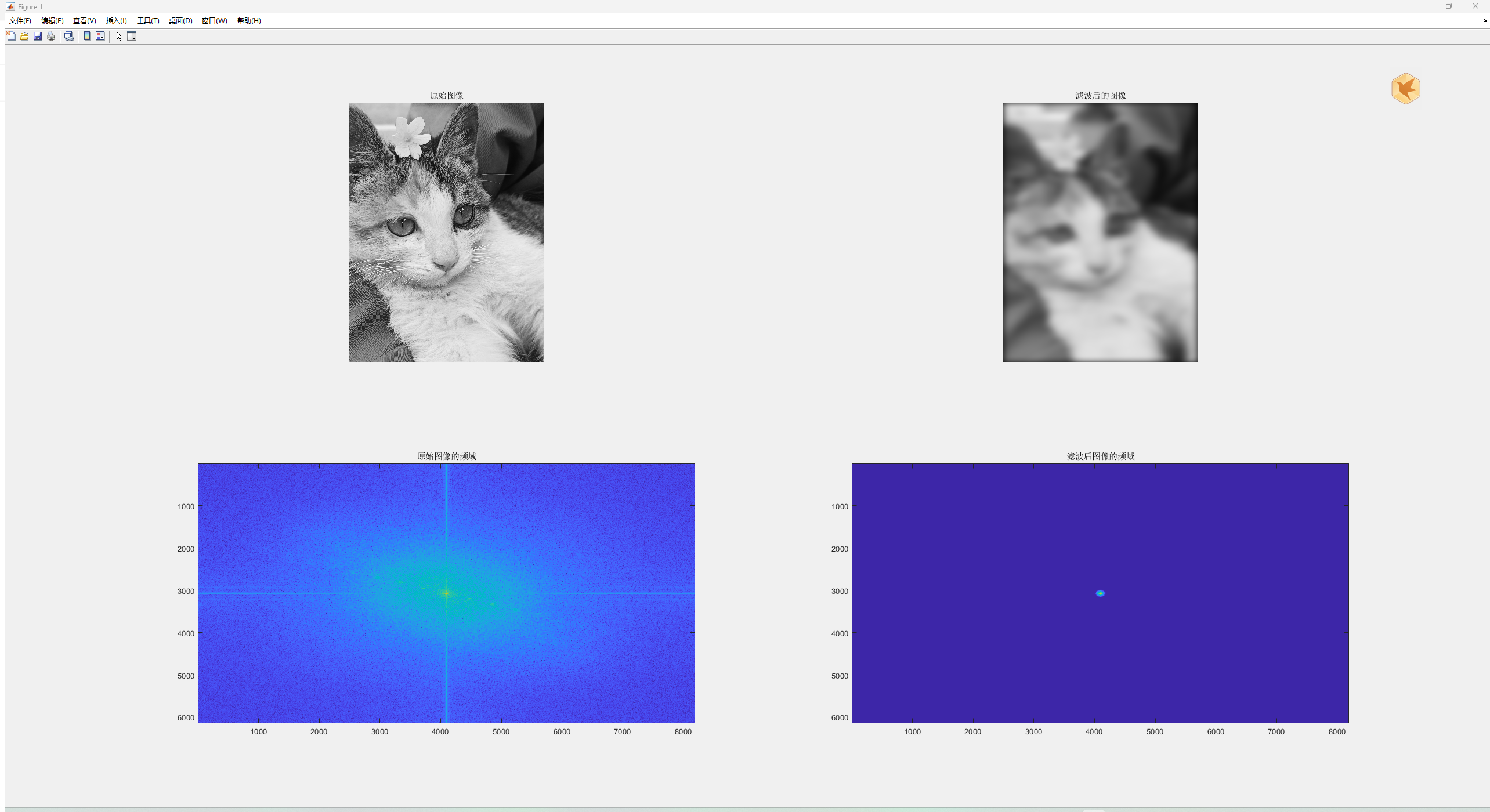
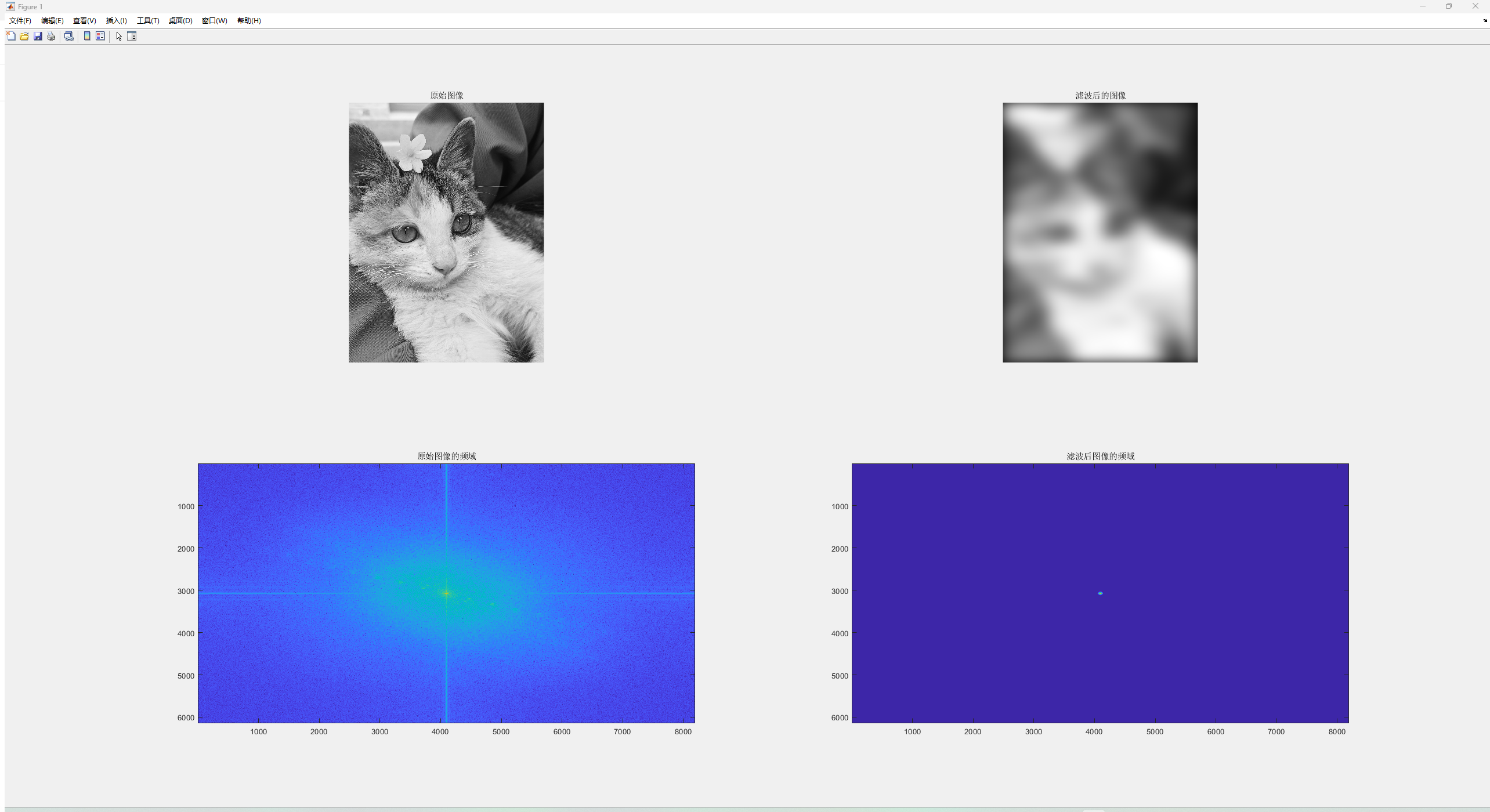
% 显示原始图像和滤波后的图像
figure;
% 显示原始图像
subplot(221);
imshow(I);
title('原始图像');
% 显示滤波后的图像
subplot(222);
imshow(L);
title('滤波后的图像');
% 显示原始图像的频域
subplot(223);
imagesc(log(1 + abs(J)));
title('原始图像的频域');
% 显示滤波后图像的频域
subplot(224);
imagesc(log(1 + abs(K)));
title('滤波后图像的频域');
(2)高斯高通滤波(Gaussian Highpass Filtering)
高斯高通滤波器通过对图像进行高斯锐化,保留图像中的高频细节,从而增强图像的边缘。其频域中的传递函数为:
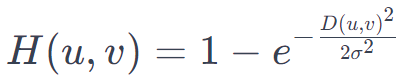
** 其中 D(u,v) 是频域中点(u,v) 到中心的距离,σ 是高斯分布的标准差。**
clear
clc
I = imread("C:\Users\14331\Desktop\微信图片_20240404190509.jpg"); % 读入图像
I = rgb2gray(I);
I=im2double(I);
M=2*size(I,1); %滤波器的行数
N=2*size(I,2); %滤波器的列数
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u, v);
D=sqrt(U.^2+V.^2);
sigma=20; %截止频率
H=1-exp(-(D.^2)./(2*(sigma^2))); %设计高斯滤波器
J=fftshift(fft2(I, size(H, 1), size(H, 2))); %空域转换到频域
K=J.*H; %滤波处理
L=ifft2(ifftshift(K)); %傅里叶反变换
L=L(1:size(I,1), 1:size(I, 2)); %改变图像大小
% 显示原始图像和滤波后的图像
figure;
% 显示原始图像
subplot(221);
imshow(I);
title('原始图像');
% 显示滤波后的图像
subplot(222);
imshow(L);
title('滤波后的图像');
% 显示原始图像的频域
subplot(223);
imagesc(log(1 + abs(J)));
title('原始图像的频域');
% 显示滤波后图像的频域
subplot(224);
imagesc(log(1 + abs(K)));
title('滤波后图像的频域');
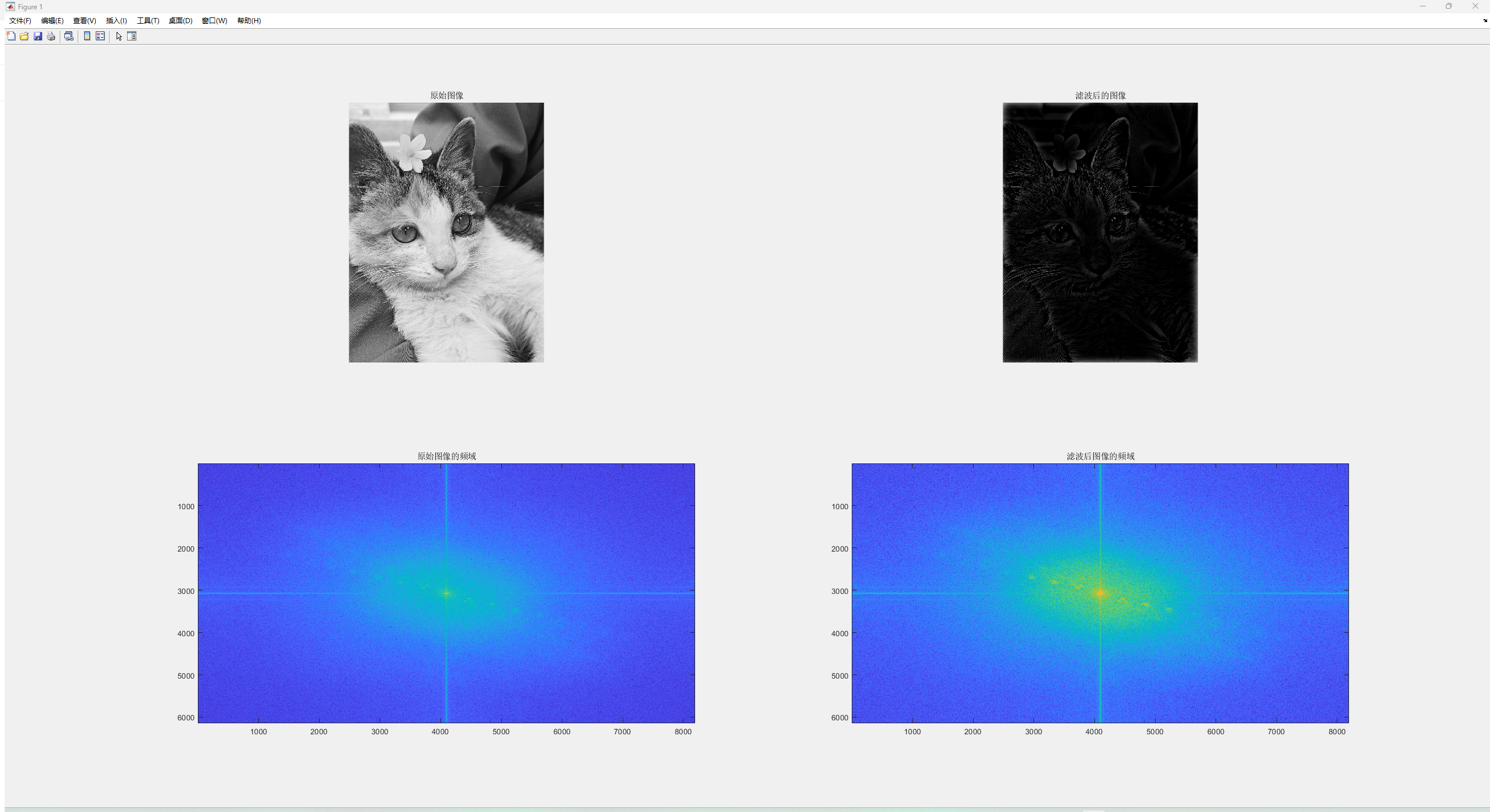
(3)高斯带通滤波(Gaussian Bandpass Filtering)
高斯带通滤波器通过在频域中选择一定范围内的频率来保留图像的一部分信息,同时滤除低频和高频成分。其传递函数为:
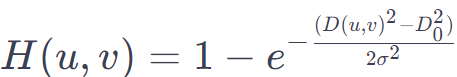
** 其中D(u,v) 是频域中点 (u,v) 到中心的距离,σ 是高斯分布的标准差,D0 是带通滤波的截止频率。**
clear
clc
I = imread("C:\Users\14331\Desktop\微信图片_20240404190509.jpg"); % 读入图像
I = rgb2gray(I);
I=im2double(I);
M=2*size(I,1); %滤波器的行数
N=2*size(I,2); %滤波器的列数
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u, v);
D=sqrt(U.^2+V.^2);
D0=5; %截止频率
sigma=10;
H=1-exp(-(D.^2-D0.^2)./(2*(sigma^2))); %设计高斯滤波器
J=fftshift(fft2(I, size(H, 1), size(H, 2))); %空域转换到频域
K=J.*H; %滤波处理
L=ifft2(ifftshift(K)); %傅里叶反变换
L=L(1:size(I,1), 1:size(I, 2)); %改变图像大小
% 显示原始图像和滤波后的图像
figure;
% 显示原始图像
subplot(221);
imshow(I);
title('原始图像');
% 显示滤波后的图像
subplot(222);
imshow(L);
title('滤波后的图像');
% 显示原始图像的频域
subplot(223);
imagesc(log(1 + abs(J)));
title('原始图像的频域');
% 显示滤波后图像的频域
subplot(224);
imagesc(log(1 + abs(K)));
title('滤波后图像的频域');
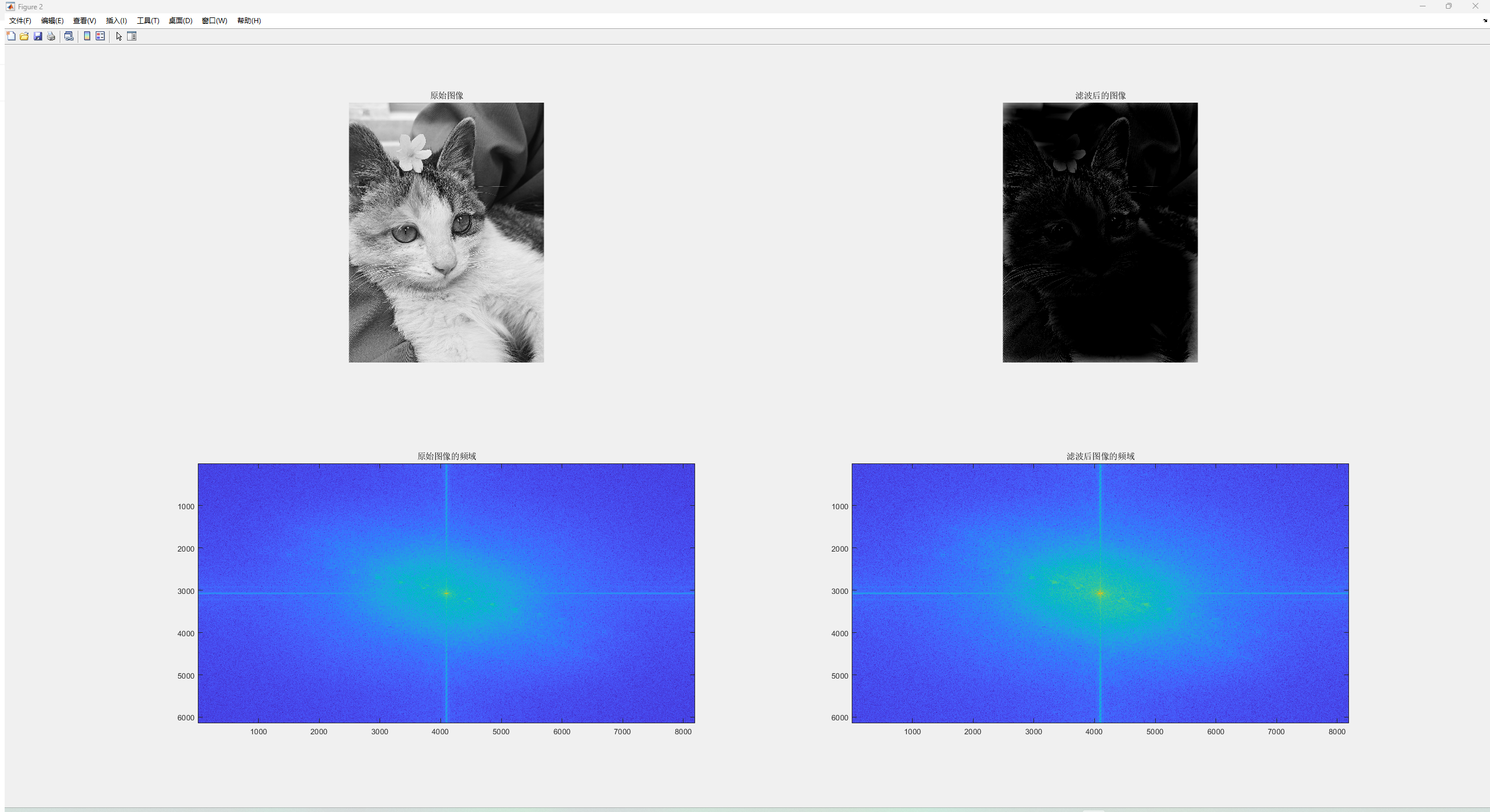
(4)高斯带阻滤波(Gaussian Bandstop Filtering)
高斯带阻滤波器与带通滤波器相反,它通过在频域中选择一定范围内的频率来滤除图像的一部分信息,同时保留低频和高频成分。其传递函数为:
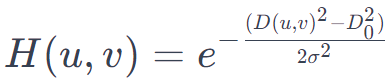
其中D(u,v) 和 D0、D1 同上,n 是滤波器的阶数。
clear
clc
I = imread("C:\Users\14331\Desktop\微信图片_20240404190509.jpg"); % 读入图像
I = rgb2gray(I);
I=im2double(I);
M=2*size(I,1); %滤波器的行数
N=2*size(I,2); %滤波器的列数
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u, v);
D=sqrt(U.^2+V.^2);
D0=5; %截止频率
sigma=10;
H=exp(-(D.^2-D0.^2)./(2*(sigma^2))); %设计高斯滤波器
J=fftshift(fft2(I, size(H, 1), size(H, 2))); %空域转换到频域
K=J.*H; %滤波处理
L=ifft2(ifftshift(K)); %傅里叶反变换
L=L(1:size(I,1), 1:size(I, 2)); %改变图像大小
% 显示原始图像和滤波后的图像
figure;
% 显示原始图像
subplot(221);
imshow(I);
title('原始图像');
% 显示滤波后的图像
subplot(222);
imshow(L);
title('滤波后的图像');
% 显示原始图像的频域
subplot(223);
imagesc(log(1 + abs(J)));
title('原始图像的频域');
% 显示滤波后图像的频域
subplot(224);
imagesc(log(1 + abs(K)));
title('滤波后图像的频域');




















 9238
9238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








