一种鲁棒的线性判别分析LDA方法，旨在解决对异常值和奇异性问题的敏感性研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

---

💥1 概述

文献来源：

摘要：传统的线性判别分析（LDA）模型存在一些挑战，比如对异常值的敏感性、类内散布矩阵奇异性问题以及对同一类别数据的高斯假设。本文提出了一种鲁棒的LDA方法，旨在解决对异常值和奇异性问题的敏感性。具体而言，我们首先使用贝叶斯风险来设计所提出的方法的优化问题。然后，所提出的基于密度的LDA（DLDA）方法利用数据密度作为先验知识，以提高对异常值的鲁棒性。该方法可以对非线性和多模态分布的数据集进行分类。此外，所提出的方法可以利用AdaBoost方法进行大数据分类。对合成和真实数据集的实验结果表明，所提出的DLDA方法在竞争方法中具有显著优势。

📚2 运行结果

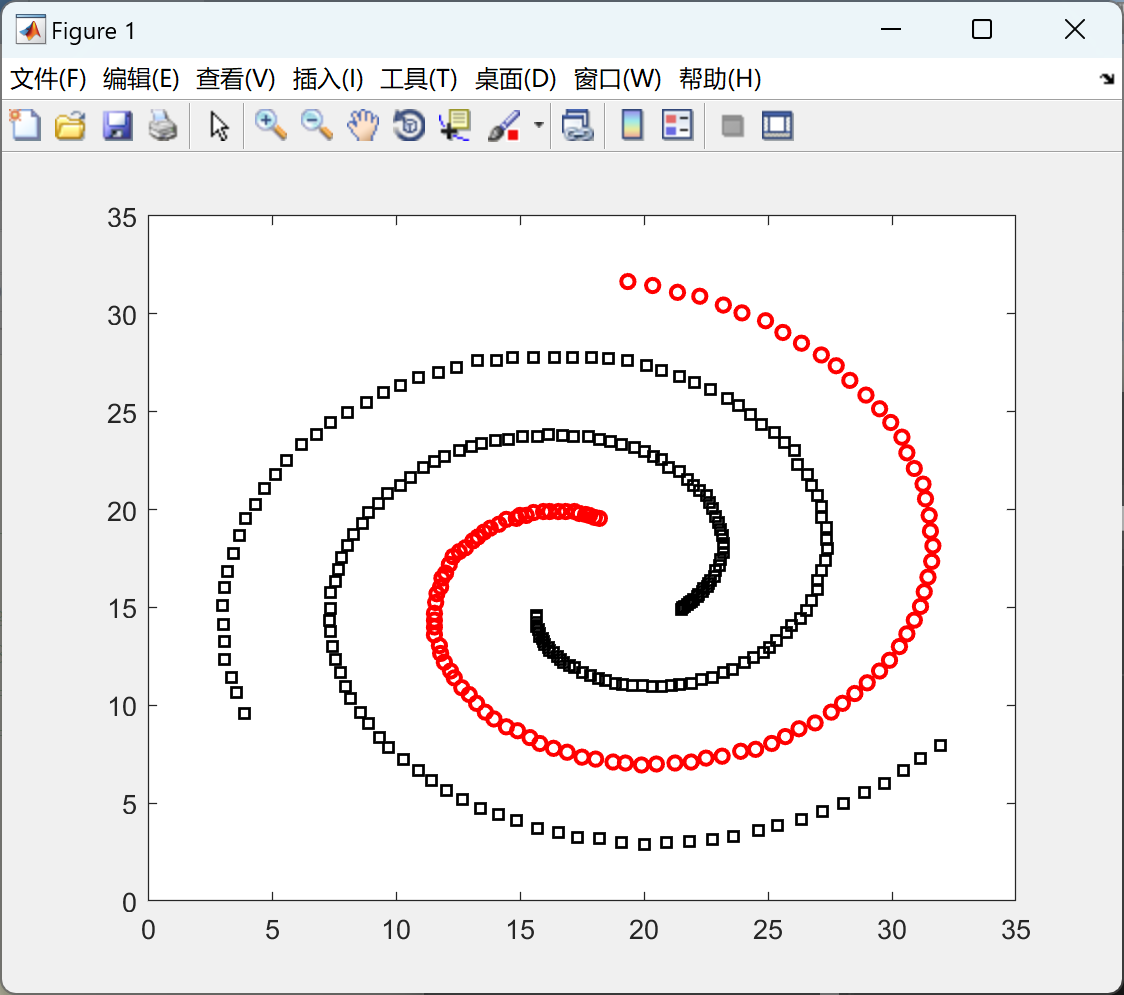
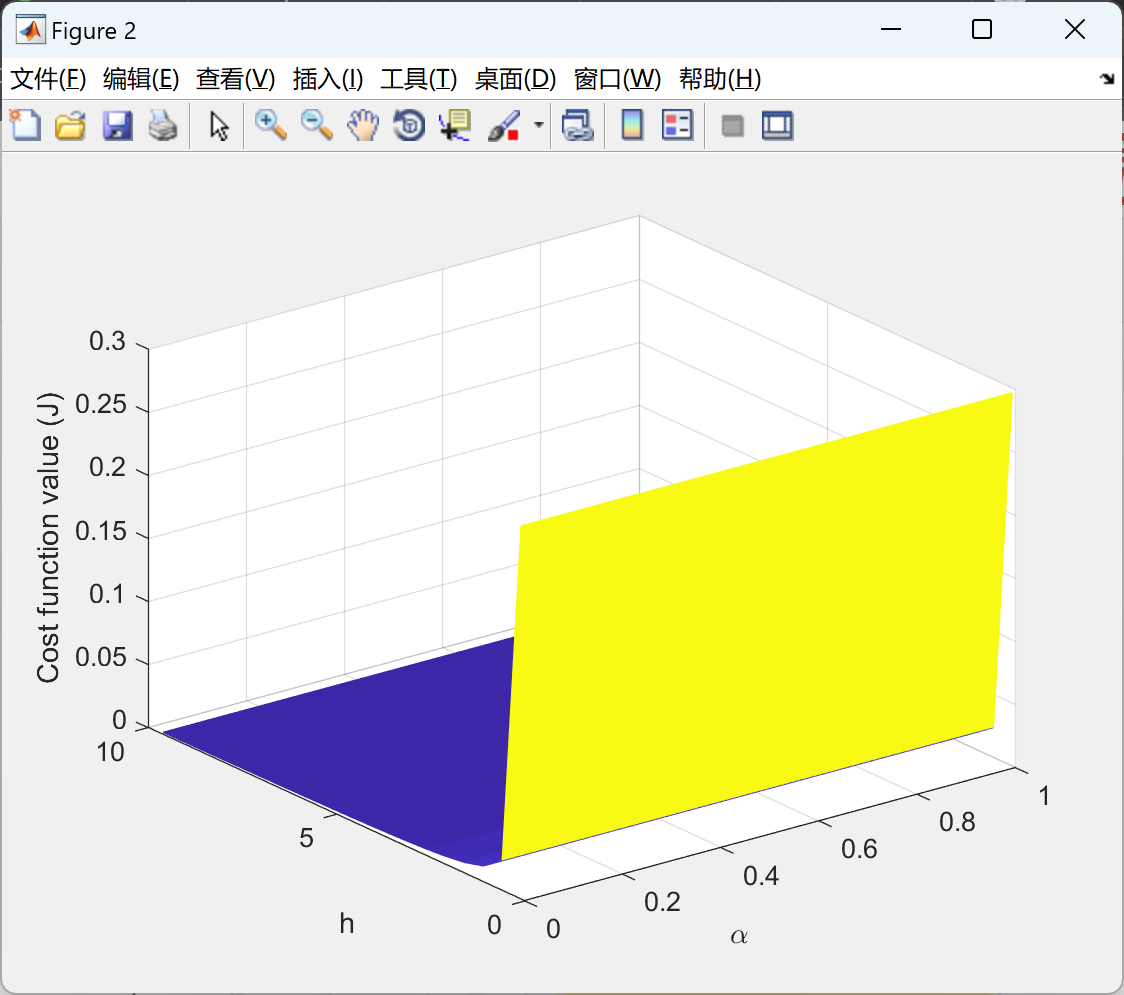
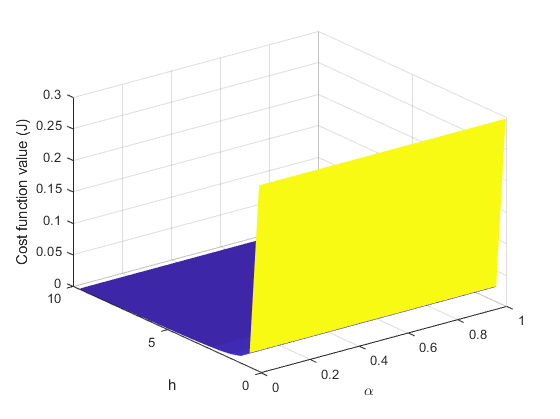
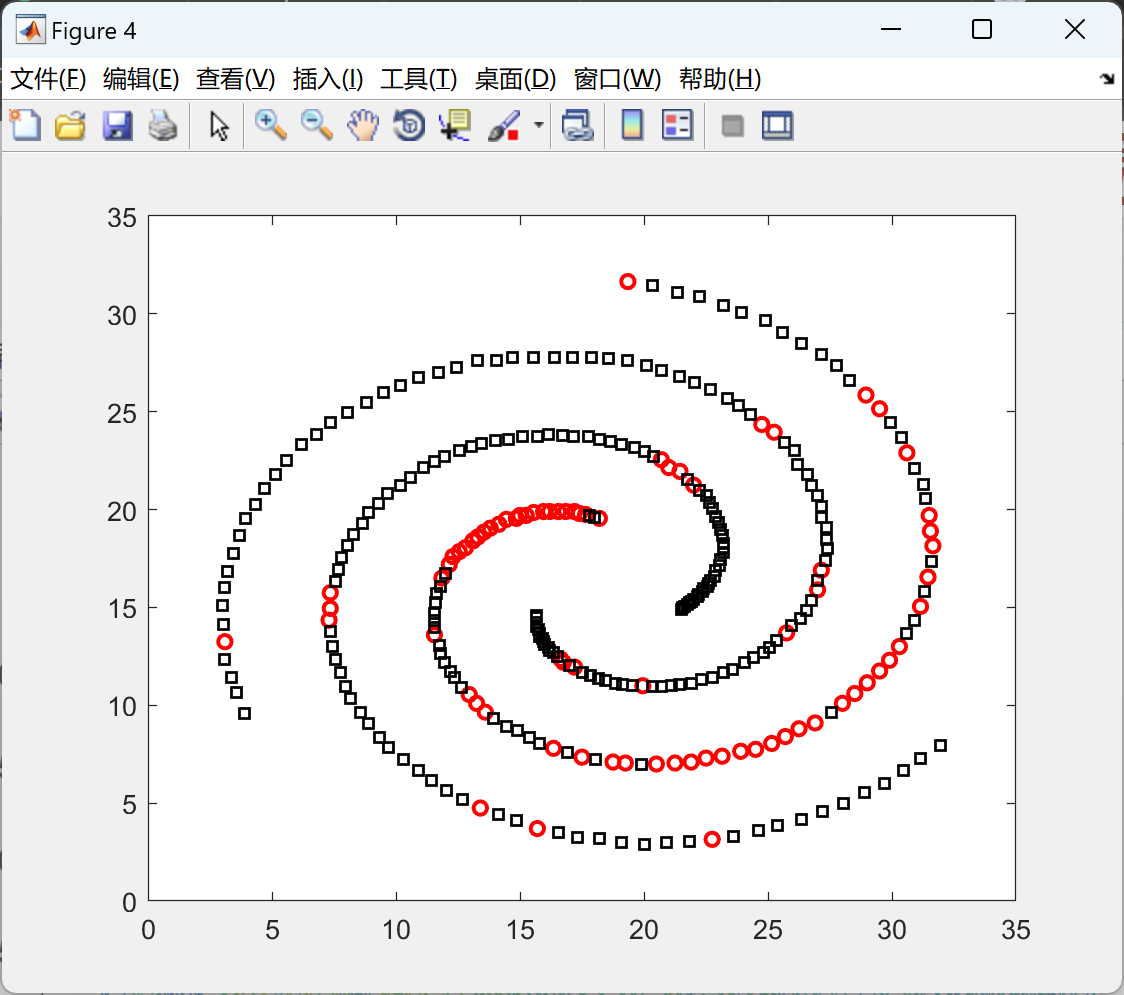
部分代码：

function [res, confusionMat]=measureEx(trueLable,predLabel,measurement,confusionMat)
% Some Popular Measurements
%   {case-insensitive}
%   {0, F, F-Measure}==>  F-Measure
%   {1, P, Precision}==>  Precision
%   {2, R, Recall}==>  Recall
%   {3, TP, True Positive Rate}==>  True Positive Rate
%   {4, FP, False Positive Rate}==>  False Positive Rate
%   {5, Se, Sensitivity}==>  Sensitivity
%   {6, Sp, Specificity}==>  Specificity
%   {7, TN, True Negative Rate}==>  True Negative Rate
%   {8, ACC}}==>  Accuracy
%   {9, N}}==>  NMI (Normalized Mutual Information)
%   {10, RI}}==>  Rand-Index
%   {11, ARI}}==>  Adjusted Rand-Index
%   {12, C}}==>  Confusion Matrix

%   <Default is 0>
if exist('measurement','var')
    measurement=lower(num2str(measurement));
else
    measurement=0;
end
if ~exist('confusionMat','var')
    confusionMat=confusionmat(trueLable,predLabel);
end
K=size(confusionMat,1);
switch measurement
    case {0, 'f', 'f-measure'}
        p=diag(confusionMat)'./sum(confusionMat);
        r=diag(confusionMat)./sum(confusionMat,2);
        res=2*(p.*r')./(p+r');
    case {'1' 'p' 'precision'}
        res=diag(confusionMat)'./sum(confusionMat);
    case {'2' 'r' 'recall'
            '3' 'tp' 'true positive rate'
            '5' 'se' 'sensitivity'}
        res=diag(confusionMat)./sum(confusionMat,2);
    case {'4' 'fp' 'false positive rate'}
        res=zeros(1,K);
        for i=1:K
            res(i)=(sum(confusionMat(:,i))-confusionMat(i,i))/sum(sum(confusionMat([1:i-1 i+1:end],:)));
        end
    case {'6' 'sp' 'specificity'

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据