leetcode编程题（5）Longest Palindromic Substring(最长回文子串)【最全解法】

最新推荐文章于 2021-11-08 00:00:00 发布
最新推荐文章于 2021-11-08 00:00:00 发布
阅读量706 收藏 3
点赞数 4
分类专栏： Java leetcode 文章标签： 最长回文子串 leetcode 最长公共子串 Manacher算法 动态规划
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/YuYunTan/article/details/84202161
版权

文章目录

Longest Palindromic Substring(最长回文子串)【最全解法】

题目（英文版）

  Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

题目（中文翻译版）

  给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

题目解析

  首先我们要了解，什么是回文字符串。回文串是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串，而 “abc” 不是。这个应该由中心对称的字符串。

  题目本身要我们做的是，在一个字符串中找到这样依据中心对称最大的字符串。

方法一： 最长公共子串法

思路

  由于 S S S中有回文串，反过来的成为 S ′ S^\prime S′。从中找到其最长公共子串，必然是最长的回文子串。但事实真的是如此是这样么？

  看下面的一个例子：

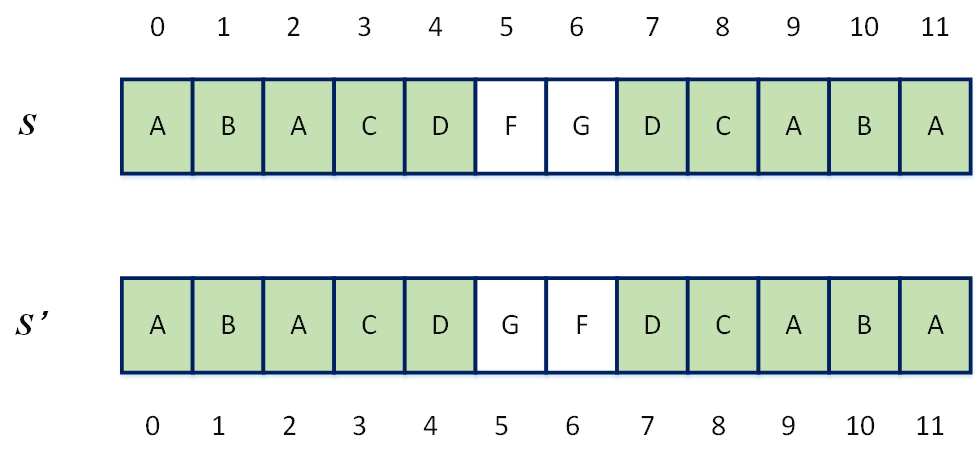
  我们得到的两者的最大公共子串是"ABACD",但这显然不是答案，该公共子串并不是回文串。

  主要的原因是在于，子串有一部分关于中间对称，而中间存在不对称的子串。

  图中可以看出，也就是说，当 S 的其他部分中存在非回文子串的反向副本且长度和大小一样但却不是回文字符串时，最长公共子串法就会失败。

  为了纠正，每当我们找到最长的公共子串的候选项时，查看当前子串 a （ A B A C D ） a（ABACD） a（ABACD）与其反向子串 b （ D C A B A ） b（DCABA） b（DCABA）,在原始 S S S中的索引是否相同。

  举个例子当前子串 a a a在原串 S S S中的索引为 0 0 0开始,而反向子串在原串 S S S中的索引却是以7开始，所以两个不是。则跳过这个候选项。反而如果是 A B A ABA ABA,则反过来还是 A B A ABA ABA，在原串的索引一致（都是0）。

  这样之后，我们就把求解变成了求解最长公共子串内容，只不过求解出来的最长公共子串需要进行上面分析的进一步处理。如果索引相同，那么我们尝试更新目前为止找到的最长回文子串；如果不同，我们就跳过这个候选项并继续寻找下一个候选。

  那么主要的核心问题就在于如何求解两个子串的最大公共子串，这里关于该公共子串的算法博文描述太多了，但博主只自己选择了动态规划的思想。

最大公共子串（动态规划）思路

  假设我们已经找到了长度为 k k k的子串，其在字符串 S S S中的下标是从 b , ⋯   , p b,\cdots,p b,⋯,p，而字符串 T T T中的下标为 d , ⋯   , q d,\cdots,q d,⋯,q。那么对于下一次的时候 p + 1 p+1 p+1和 q + 1 q+1 q+1的时候，我们分别判断这两个下标分别在这两个字符串 S S S和 T T T中是否相等，如果相等则在原基础上，最大公共子串长度加1。

  这样我们就得到了递推公式，而且很容易得到关于动态规划DP的表达式。

L C S u f f ( S b … p , T d … q ) = { L C S u f f ( S b … p − 1 , T d … q − 1 ) + 1 i f S [ p ] = T [ q ] 0 o t h e r w i s e LCSuff(S_{b\dots p},T_{d\dots q})=\begin{cases}LCSuff(S_{b\dots p-1},T_{d\dots q-1})+1& if \quad S[p]=T[q]\\0& otherwise\end{cases} LCSuff(Sb…p​,Td…q​)={LCSuff(Sb…p−1​,Td…q−1​)+10​ifS[p]=T[q]otherwise​

  在实现中我们是构建一张二维表。我们称为DP表 L [ ] [ ] L[][] L[][]，假设而其值则是保存最长公共子串的长度。我们假设当前的表值 L [ i ] [ j ] = k ( k > 0 ) L[i][j]=k(k>0) L[i][j]=k(k>0)时，那么意味着在字符串 S S S中下标从 i − k + 1 , i i-k+1,i i−k+1,i和在字符串 T T T中从下标 j − k + 1 , j j-k+1,j j−k+1,j是长度为 k k k的相等的公共子串（不一定是最长，因为还没确定大小是表中最大的）。

  我们举个例子去说明。

  假设我们有两个子串"ABAB"和“BABA”：

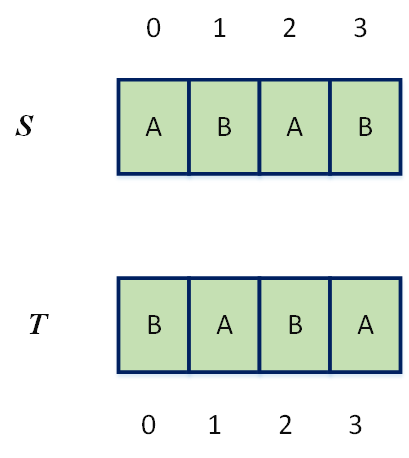
  刚开始的时候，我们的二维表全都是0，对于我们后面的实现的时候，我们不用多余出的一行。

ABAB
00000
B00000
A00000
B00000
A00000

  接下来，我们进行判断，开始将指针推动，按照DP表的设定，字符串认为是从1开始，所以为了描述清楚，本次也就认为字符串从1开始。

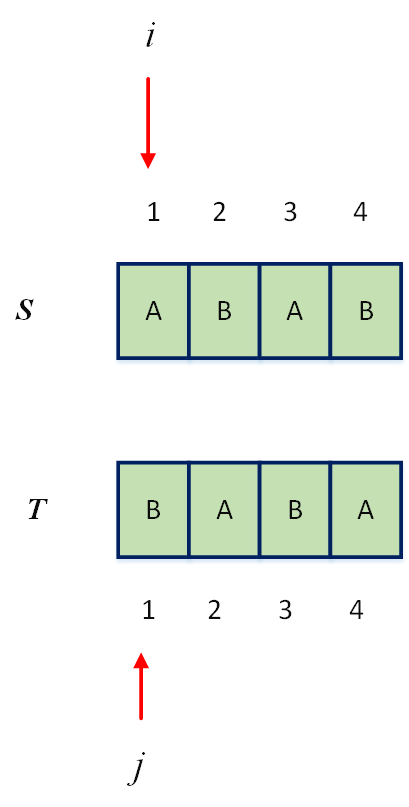
  每次移动的填表的时候，都会用到上一次的结果。

  如果字符串相同则会认为是共同子串，这样之后，我们可以得到下面的表。请问你看出来什么规律了么？

ABAB
00000
B00101
A01020
B00203
A01030

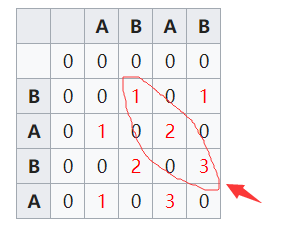
  大家可以看出来，这个是个对角线对称的矩阵【但是不是每次运用这种DP结构一直都是斜对称矩阵，大家可以动手试试】，第二，有连续子串的地方，必然是这样的斜线结构的递增类型。这是怎么回事？请看递推式子：

L C S u f f ( S b … p , T d … q ) = L C S u f f ( S b … p − 1 , T d … q − 1 ) + 1 LCSuff(S_{b\dots p},T_{d\dots q})=LCSuff(S_{b\dots p-1},T_{d\dots q-1})+1 LCSuff(Sb…p​,Td…q​)=LCSuff(Sb…p−1​,Td…q−1​)+1

  如果我们知道 L C S u f f ( S b … p − 1 , T d … q − 1 ) LCSuff(S_{b\dots p-1},T_{d\dots q-1}) LCSuff(Sb…p−1​,Td…q−1​)已经是连续子串了，那么又知道 S [ p ] = T [ q ] S[p]=T[q] S[p]=T[q]，自然而言， L C S u f f ( S b … p , T d … q ) LCSuff(S_{b\dots p},T_{d\dots q}) LCSuff(Sb…p​,Td…q​)也是连续子串，注意看下标位置，我们这两个地方的下标在表中分别表示为 L [ p − 1 ] [ q − 1 ] L[p-1][q-1] L[p−1][q−1]和 L [ p ] [ q ] L[p][q] L[p][q]，那么很容易得到这两个是沿着一条与中心对角线平行的方向的延续生长。这就是DP的优点了，可以利用了之前的结果的原因。

  这样算法也就出来了，只要保存出在该表最大值时的下标 i , j i,j i,j，就能得到两个字符串最大公共长度为 k k k时的最大公共子串。

  但是在我们用其求解最大回文串的时候，必然而然的，需要进行判断才能解决。判断的方法在前面已有描述。

  我们在算法实现的过程中，不会采用字符串下标为1开始的字符串，为0开始。而且我们的最大回文串长度必为1，所以设定初始化的时候为1。也就是我们使用了求解最大公共子串的变体，在下面会给出具体代码。

算法复杂度
  • 时间复杂度： O ( n 2 ) \mathcal{O}(n^2) O(n2)，因为DP表是二维数组，对表中每个元素进行赋值过程中还要进行判断，其中有字符串翻转的部分则可以忽略不计，主要还是 O ( n 2 ) \mathcal{O}(n^2) O(n2)
  • 空间复杂度： O ( n 2 ) \mathcal{O}(n^2) O(n2)，还是因为DP表是二维数组。可以改进为 O ( n ) \mathcal{O}(n) O(n)
算法代码
会超时线下没问题的该算法代码
package Longest_Palindromic_Substring.four;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;

/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
	    String s_invert = new StringBuilder(s).reverse().toString();
	    return LCSubstr(s,s_invert);    
    }
	


	private String LCSubstr(String s, String s_invert) {
		int L[][] = new int [s.length()+1][s_invert.length()+1];
		int maxLength=1;
		String ret="";
		ArrayList<String> R = new ArrayList<>();
		for(int i=0;i<s.length();i++) {
			for(int j=0;j<s_invert.length();j++) {
				if(s.charAt(i) == s_invert.charAt(j)) {
					if(i == 0 || j == 0) {
						L[i][j]=1;
					}else {
						L[i][j]=L[i-1][j-1]+1;
					}
					if(L[i][j] >= maxLength) {	
						int start = i-L[i][j]+1;
						// 可能是候选项
						String temp = s.substring(start,start+L[i][j]);
						String temp_inv = new StringBuilder(temp).reverse().toString();
						if(s.indexOf(temp) == s.indexOf(temp_inv)) {
							// 更新
							R.add(temp);//符合条件的
						}
					}
				}else {
					L[i][j]=0;
				}
			}
		}
		Collections.sort(R, new Comparator<String>() {

			@Override
			public int compare(String o1, String o2) {
				return o2.length()-o1.length();
			}
			
		});
		
		return R.get(0);
	}



	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome("cccc"));
		System.out.println(n1.longestPalindrome("abacab"));// "bacab"*/
		System.out.println(n1.longestPalindrome("abcdbbfcba"));// "bb"
		System.out.println(n1.longestPalindrome("qrrohydrmbvtuwstgkobyzjjtdtjroq"));//jtdtj
				
	}
	
}
改进并通过的代码

  主要是得到的候选项太多没进行筛选处理的话，进行排序耗费时间太多。所以对之进行改进，而且取消排序的原因。

package Longest_Palindromic_Substring.four;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;

/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
	    String s_invert = new StringBuilder(s).reverse().toString();
	    if(s.equals(s_invert))return s;
	    return LCSubstr(s,s_invert);    
    }
	


	private String LCSubstr(String s, String s_invert) {
		int L[][] = new int [s.length()+1][s_invert.length()+1];
		int maxLength=1;
		int currentMaxLength = 0;
		String ret="";
		ArrayList<String> R = new ArrayList<>();
		for(int i=0;i<s.length();i++) {
			for(int j=0;j<s_invert.length();j++) {
				if(s.charAt(i) == s_invert.charAt(j)) {
					if(i == 0 || j == 0) {
						L[i][j]=1;
					}else {
						L[i][j]=L[i-1][j-1]+1;
					}
					if(L[i][j] >= currentMaxLength) {	
						int start = i-L[i][j]+1;
						// 可能是候选项
						String temp = s.substring(start,start+L[i][j]);
						String temp_inv = new StringBuilder(temp).reverse().toString();
						if(L[i][j]>currentMaxLength && s.indexOf(temp) == s.indexOf(temp_inv)) {
							// 更新
							currentMaxLength = temp.length();
							R.add(temp);//符合条件的
						}
					}
				}else {
					L[i][j]=0;
				}
			}
		}
		
		return R.get(R.size()-1);
	}



	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome("cccc"));
		System.out.println(n1.longestPalindrome("abacab"));// "bacab"*/
		System.out.println(n1.longestPalindrome("abcdbbfcba"));// "bb"
		System.out.println(n1.longestPalindrome("qrrohydrmbvtuwstgkobyzjjtdtjroq"));//jtdtj			
	}
}

  在这里面，还可以做稍微的改进，比如由于我们的输入很特殊，一个串和其反向串，所以最大公共子串必然大于1，所以可以设置currentMaxLength初始化为1，这样减少了一次进入判断的操作。另外空间上，最简单是不要ArrayList，毕竟我们只取一个符合条件的结果，所以可以用一个变量来解决。

  本质上来说，该方法是求最大回文串，只不过我们这里采取的是空间复杂度达到 O ( n 2 ) \mathcal{O}(n^2) O(n2)，但是目前已经有一些方法可以将之降到 O ( n ) \mathcal{O}(n) O(n)，这里博主不再累赘描述，而且可以根据这张表的结构进行优化改进，有兴趣的人可以自行求解。欢迎在博文下方评论贴上自己代码。

方法二：镜像中心扩展方法

  我们知道，回文字符串是以中心对称的字符串。这样我们可以利用这样的特性，以中心展开。

思路

  详细的来说，我们假设当前的字符是中心字符，然后向字符串前和后分别遍历，看两者是否相等，若相等，则是回文串，一直到不是为止，这样就能得到以该字符为中心的最大回文串。假设我们有 n n n个字符的字符串，这样的操作则需要进行 n n n次【为了不失一般性，我们认为单个字符也可以是回文串，只不过不是最长的】。

  但是值得注意的是，因为对称中心可能是两个字符，也就是字符串如果是偶数字符串长度，所以这也是考虑的因素。

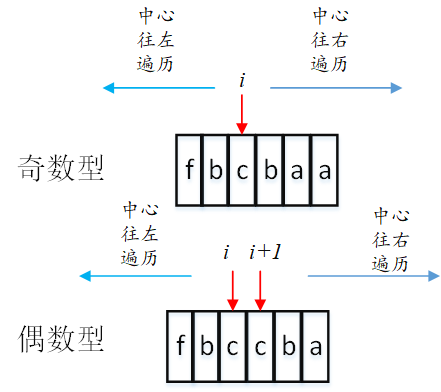
  该算法中，我们以下标往左往右进行扩展，分别找到以该字符为中心镜像的奇偶最长回文子串，然后这两个进行对比，我们用end和start保存当前最大的方案，而且两者之差是其最大方案的长度。顺序遍历该字符串，直到遍历完毕，就能将最大回文子串找到。

算法复杂度
  • 时间复杂度： O ( n 2 ) \mathcal{O}(n^2) O(n2)，因为我们遍历字符串是 O ( n ) \mathcal{O}(n) O(n),每次遍历字符串，可能会达到 O ( n ) \mathcal{O}(n) O(n)的长度，这样情况下，我们的复杂度是 O ( n 2 ) \mathcal{O}(n^2) O(n2)
  • 空间复杂度： O ( 1 ) \mathcal{O}(1) O(1)，由于并不需要数组之类保存，只需要一些遍历，所以需要的空间并不大。
算法代码
/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
	    int start = 0, end = 0;
	    for (int i = 0; i < s.length(); i++) {
	        int len1 = expandAroundCenter(s, i, i); // 奇数情况
	        int len2 = expandAroundCenter(s, i, i + 1);// 偶数情况
	        int len = Math.max(len1, len2);
	        if (len > end - start) {// 保存解决方案的结果
	            start = i - (len - 1) / 2;// 首
	            end = i + len / 2;// 尾
	        }
	    }
	    return s.substring(start, end + 1);
    }
	
	private int expandAroundCenter(String s, int left, int right) {
		int L = left, R = right;
	    while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
	        L--;// 向前展开
	        R++;// 向后展开
	    }
	    return R - L - 1;// 展开后的最大回文串长度
	}

	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));
		System.out.println(n1.longestPalindrome("cbbd"));
		System.out.println(n1.longestPalindrome("abcdf"));
	}
	
}

方法三：暴力法

  博主觉得，暴力法应该是最简单又最粗暴的方法，实在是三重循环又不费脑子。不过看见题目说的，字符串最长为 1000 1000 1000，就算三次方也不过是 1 0 9 10^9 109次方搞定，目前计算机资源庞大，倒是可以很快完成。

  所以该方法可以实现，不过在面试的过程中，如果有暴力法能求解的最好是暴力，然后再想法进行优化。但是这个方法在leetcode会超时。

思路

  暴力选择出所有子串，然后判断是不是回文字符串。

算法复杂度
  • 时间复杂度： O ( n 3 ) \mathcal{O}(n^3) O(n3)，假设 n n n是输入的字符串长度，则需要 C n 2 = n ( n − 1 ) 2 C_n^2=\frac{n(n-1)}{2} Cn2​=2n(n−1)​种子字符串，这是我们在长度为 n n n的字符串中选择两个下标，标记为起始和节点下标，这是 O ( n 2 ) \mathcal{O}(n^2) O(n2)。而验证每个子串是回文串需要 O ( n ) \mathcal{O}(n) O(n)，故而是 O ( n 3 ) \mathcal{O}(n^3) O(n3)。
  • 空间复杂度： O ( 1 ) \mathcal{O}(1) O(1)，由于并不需要数组之类保存，只需要一些遍历，所以需要的空间并不大。
算法代码
会超时无法通过的暴力破解
/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
		if(s.length() == 1) return s;
	    int start = 0, end = 0,len=1;
	    for (int i = 0; i < s.length(); i++) {
	        for(int j=i+len;j<= s.length();j++) {
	        	String temp = s.substring(i,j);
	        	if(isPalindrome(temp)) {
		        	if (temp.length() > end - start) {// 保存解决方案的结果
	    	            start = i;// 首
	    	            end = j;// 尾
		        	}
	        	}

	        }
	    }
	    return s.substring(start, end);
    }
	
	private boolean isPalindrome(String s) {
		int start=0,end=s.length()-1;
		while(start <= end) {
			if(s.charAt(start++) != s.charAt(end--))return false;
		}
		return true;
	}

	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome(
				"gphyvqruxjmwhonjjrgumxjhfyupajxb"
				+ "jgthzdvrdqmdouuukeaxhjumkmmhdgl"
				+ "qrrohydrmbvtuwstgkobyzjjtdtjroq"
				+ "pyusfsbjlusekghtfbdctvgmqzeybnwz"
				+ "lhdnhwzptgkzmujfldoiejmvxnorvbiu"
				+ "bfflygrkedyirienybosqzrkbpcfidvk"
				+ "kafftgzwrcitqizelhfsruwmtrgaocjc"
				+ "yxdkovtdennrkmxwpdsxpxuarhgusizm"
				+ "wakrmhdwcgvfljhzcskclgrvvbrkesoj"
				+ "yhofwqiwhiupujmkcvlywjtmbncurxxm"
				+ "pdskupyvvweuhbsnanzfioirecfxvmgc"
				+ "pwrpmbhmkdtckhvbxnsbcifhqwjjczfo"
				+ "kovpqyjmbywtpaqcfjowxnmtirdsfeuj"
				+ "yogbzjnjcmqyzciwjqxxgrxblvqbutqi"
				+ "ttroqadqlsdzihngpfpjovbkpeveidjp"
				+ "fjktavvwurqrgqdomiibfgqxwybcyovy"
				+ "sydxyyymmiuwovnevzsjisdwgkcbsook"
				+ "barezbhnwyqthcvzyodbcwjptvigcpha"
				+ "wzxouixhbpezzirbhvomqhxkfdbokblq"
				+ "mrhhioyqubpyqhjrnwhjxsrodtblqxkh"
				+ "ezubprqftrqcyrzwywqrgockioqdmzuq"
				+ "jkpmsyohtlcnesbgzqhkalwixfcgyeqd"
				+ "zhnnlzawrdgskurcxfbekbspupbduxqx"
				+ "jeczpmdvssikbivjhinaopbabrmvscth"
				+ "voqqbkgekcgyrelxkwoawpbrcbszelnx"
				+ "lyikbulgmlwyffurimlfxurjsbzgddxbg"
				+ "qpcdsuutfiivjbyqzhprdqhahpgenjkb"
				+ "iukurvdwapuewrbehczrtswubthodv"));//jtdtj
	}
	
}
改进的可通过的暴力法

  思路是在暴力的基础上，将一些肯定不会是最后结果的答案去掉，首先将当前最大的回文子串的长度保存，下一次判断的回文子串必然要大于当前结果的最大回文子串的长度才会更新。依旧是暴力的本质，仍然达到 O ( n 3 ) \mathcal{O}(n^3) O(n3)，只是比纯暴力减少了许多需要的判断。

/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
		if(s.length() == 1) return s;
	    int start = 0, end = 0,len=1;
	    for (int i = 0; i < s.length(); i++) {
	        for(int j=i+len;j<= s.length();j++) {
	        	String temp = s.substring(i,j);
	        	if (temp.length() > end - start && isPalindrome(temp)) {// 保存解决方案的结果
	    	            start = i;// 首
	    	            end = j;// 尾
	    	            len = end - start;
	    	    }
	        }
	    }
	    return s.substring(start, end);
    }
	
	private boolean isPalindrome(String s) {
		int start=0,end=s.length()-1;
		while(start <= end) {
			if(s.charAt(start++) != s.charAt(end--))return false;
		}
		return true;
	}

	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome(
				"gphyvqruxjmwhonjjrgumxjhfyupajxb"
				+ "jgthzdvrdqmdouuukeaxhjumkmmhdgl"
				+ "qrrohydrmbvtuwstgkobyzjjtdtjroq"
				+ "pyusfsbjlusekghtfbdctvgmqzeybnwz"
				+ "lhdnhwzptgkzmujfldoiejmvxnorvbiu"
				+ "bfflygrkedyirienybosqzrkbpcfidvk"
				+ "kafftgzwrcitqizelhfsruwmtrgaocjc"
				+ "yxdkovtdennrkmxwpdsxpxuarhgusizm"
				+ "wakrmhdwcgvfljhzcskclgrvvbrkesoj"
				+ "yhofwqiwhiupujmkcvlywjtmbncurxxm"
				+ "pdskupyvvweuhbsnanzfioirecfxvmgc"
				+ "pwrpmbhmkdtckhvbxnsbcifhqwjjczfo"
				+ "kovpqyjmbywtpaqcfjowxnmtirdsfeuj"
				+ "yogbzjnjcmqyzciwjqxxgrxblvqbutqi"
				+ "ttroqadqlsdzihngpfpjovbkpeveidjp"
				+ "fjktavvwurqrgqdomiibfgqxwybcyovy"
				+ "sydxyyymmiuwovnevzsjisdwgkcbsook"
				+ "barezbhnwyqthcvzyodbcwjptvigcpha"
				+ "wzxouixhbpezzirbhvomqhxkfdbokblq"
				+ "mrhhioyqubpyqhjrnwhjxsrodtblqxkh"
				+ "ezubprqftrqcyrzwywqrgockioqdmzuq"
				+ "jkpmsyohtlcnesbgzqhkalwixfcgyeqd"
				+ "zhnnlzawrdgskurcxfbekbspupbduxqx"
				+ "jeczpmdvssikbivjhinaopbabrmvscth"
				+ "voqqbkgekcgyrelxkwoawpbrcbszelnx"
				+ "lyikbulgmlwyffurimlfxurjsbzgddxbg"
				+ "qpcdsuutfiivjbyqzhprdqhahpgenjkb"
				+ "iukurvdwapuewrbehczrtswubthodv"));//jtdtj
	}
	
}

方法四：动态规划

  在暴力法的基础上的改进，利用了中间判断的结果。比如已知”bab“是回文字符串，那么很容易得到"ababa"一定是回文字符串，因为其左首字母和右尾字母是一样的。这样就减少了回文循环的判断，利用起了中间判断的结果。

思路

  利用二维Boolean数组 P [ i ] [ j ] P[i][j] P[i][j]保存中间结果，对于 P [ i ] [ j ] P[i][j] P[i][j]的定义如下：

P ( i , j ) = { t r u e , 如 果 子 串 s i ⋯ s j 是 回 文 串 f a l s e , 其 他 情 况 P(i,j)=\begin{cases}true,&amp; 如果子串s_i\cdots s_j是回文串\\false,&amp;其他情况\end{cases} P(i,j)={true,false,​如果子串si​⋯sj​是回文串其他情况​

  那么如果我们知道了 P ( i , j ) P(i,j) P(i,j)的递推动态公式

P ( i , j ) = ( P ( i + 1 , j − 1 ) &ThickSpace; a n d &ThickSpace; S i = = S j ) P(i,j)=(P(i+1,j-1) \;{\rm and} \;S_i==S_j) P(i,j)=(P(i+1,j−1)andSi​==Sj​)

  我们知道

P ( i , i ) = t r u e P(i,i)=true P(i,i)=true

  可以直接递推 P ( i , i + 1 ) = ( S i = = S i + 1 ) P(i,i+1)=(S_i == S_{i+1}) P(i,i+1)=(Si​==Si+1​)

  我们首先初始化一字母和二字母的回文，然后找到所有三字母的回文，以此类推。

算法复杂度分析
  • 时间复杂度： O ( n 2 ) \mathcal{O}(n^2) O(n2)，每次遍历填入表中元素并保存期间最大值
  • 空间复杂度： O ( n 2 ) \mathcal{O}(n^2) O(n2)，使用了 n × n n\times n n×n的空间来存储中间元素
算法代码
/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
	    boolean P[][] = new boolean [s.length()][s.length()];// 默认全为false
	    for(int i=0;i<s.length();i++)P[i][i]=true;// 长度为1的子串
	    int len = 1,start=0;
	    for(int i=0;i<s.length()-1;i++) {// 长度为2的子串
	    	P[i][i+1]= (s.charAt(i) == s.charAt(i+1));
	    	if(P[i][i+1]) {//符合条件的进行记录
	    		len = 2;
	    		start = i;
	    	}
	    }
	    for(int l=len+1;l<=s.length();l++) {
	    	for(int i=0;i<=s.length()-l;i++) {// 保证i+1绝不大于s.length()
	    		int j =i+l-1;// 保证了j>i
	    		P[i][j] = P[i+1][j-1]?(s.charAt(i) == s.charAt(j)):P[i+1][j-1];
	    		if(P[i][j] && l>len) {
	    			len =l;
	    			start = i;
	    		}
	
	    	}
	    }
	    return s.substring(start, start+len);
    }
	


	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome("cccc"));
		System.out.println(n1.longestPalindrome("abacab"));// "bacab"
		System.out.println(n1.longestPalindrome("qrrohydrmbvtuwstgkobyzjjtdtjroq"));//jtdtj
				
	}
	
}

方法五：Manacher 算法（最优）

  这是一个复杂度为 O ( n ) \mathcal O(n) O(n) 的 Manacher 算法，又称为 “马拉车”算法。。将之编码成功很费时，博主废了不少劲。不过想了解更为清楚的，查看维基百科关于Manacher的描述。

思路

  思想和KMP扩展算法类似。下面描述参考了该文章。并且加上博主自身的理解，我只想到前面的四种算法，该算法的确有点神奇。

  考虑最坏的情况是多个回文相互重叠的输入。例如，输入： “ a a a a a a a a a ” “aaaaaaaaa” “aaaaaaaaa”和 “ c a b c b a b c b a b c b a ” “cabcbabcbabcba” “cabcbabcbabcba”。实际上，我们可以利用回文的对称属性并避免一些不必要的计算。

  首先，通过在字母之间插入一个特殊字符“＃”将输入字符串 S S S转换为另一个字符串 T T T。 这样做的原因后面会解释，但值得一提的是，要求的字符串中原本无“＃”。

  例如： S = “ a b a a b a ” S =“abaaba” S=“abaaba”， T = “ # a # b # a # a # b # a # ” T =“ \#a\#b\#a\#a\#b\#a\#” T=“#a#b#a#a#b#a#”。

  为了找到最长的回文子串，我们需要在每个 T i T_i Ti​周围扩展，使得 T i − d ⋯ T i + d T_{i-d}\cdots T_{i+d} Ti−d​⋯Ti+d​形成回文。您应该立即看到 d d d是以 T i T_i Ti​为中心的回文长度。

  我们将中间结果存储在数组P中，其中 P [ i ] P[i] P[i]等于 T i T_i Ti​处的回文中心的长度。最长的回文子串将是 P P P中的最大元素。

  使用上面的例子，我们填充P如下（从左到右）：

T = #a#b#a#a#b#a#
P = 0103016103010

  看着P，我们立即看到最长的回文是“abaaba”，如 P 6 = 6 P_6=6 P6​=6所示。

  你可以看到，无论是奇数还是偶数的字符串，变成从数组 P P P后处理使得处理效果变得一致，所以在字母之间插入特殊字符#后才用这个算法可以一同处理了奇数和偶数长度的回文。

  现在，想象一下你在回文“abaaba”的中心画一条想象的垂直线。你注意到P中的数字是围绕这个中心对称的吗？不仅如此，尝试另一个回文“aba”，这些数字也反映出类似的对称属性。而这并非巧合。这只适用于条件，但无论如何，我们有很大的进步，因为我们可以消除重新计算 P [ i ] P[i] P[i]的部分。

  让我们继续进行一个稍微复杂的例子，其中有一些重叠的回文，其中 S = “ b a b c b a b c b a c c b a ” S =“babcbabcbaccba” S=“babcbabcbaccba”。

  请你注意上图中， T T T是从 S = “ b a b c b a b c b a c c b a ” S =“babcbabcbaccba” S=“babcbabcbaccba”转换而来。假设已达到表 P P P部分完成的状态。实线垂直线表示回文 “ a b c b a b c b a ” “abcbabcba” “abcbabcba”的中心 ( C ) (C) (C)。两条虚线垂直线分别表示其左 （ L ） （L） （L）和右 （ R ） （R） （R）边缘。你在下标 i i i，和它在 C C C周围的镜像下标是 i ′ i^\prime i′。问题来了，如何有效地计算 P [ i ] P[i] P[i]？

  假设我们已经到达下标 i = 13 i = 13 i=13，我们需要计算 P [ 13 ] P [13] P[13]（由问号 ？ ？ ？表示）。我们首先看一下它在回文串的中心 C C C周围的镜像下标，即下标 i ′ = 9 i^\prime=9 i′=9。

  上图的两条绿色实线表示以 i i i和 i ′ i^\prime i′为中心的两个回文区域的覆盖区域。我们看看 C C C周围的镜像下标，即下标 i ′ i^\prime i′。 P [ i ′ ] = P [ 9 ] = 1 P[i^\prime]=P[9]=1 P[i′]=P[9]=1,很明显， P [ i ] P[i] P[i]也必须为1，这是由于回文的中心周围的对称性质。

  实际上， C C C之后的三个元素都遵循对称性（即 P [ 12 ] = P [ 10 ] = 0 P [12] = P [10] = 0 P[12]=P[10]=0， P [ 13 ] = P [ 9 ] = 1 P [13] = P [9] = 1 P[13]=P[9]=1， P [ 14 ] = P [ 8 ] = 0 P [14] = P [8] = 0 P[14]=P[8]=0）。

  现在我们在下标 i = 15 i = 15 i=15。 P [ i ] P [i] P[i]的值是多少？如果我们遵循对称属性， P [ i ] P [i] P[i]的值应该与 P [ i ′ ] = 7 P [i^\prime] = 7 P[i′]=7相同。但这是错误的。如果我们在 T 15 T_{15} T15​处围绕中心扩展，它形成了一个回文 “ a ＃ b ＃ c ＃ b ＃ a ” “a＃b＃c＃b＃a” “a＃b＃c＃b＃a”，它实际上比它的对称对应物更短。为什么？

  看上图在下标 i i i和 i ′ i^\prime i′处围绕中心重叠彩色线。由于 C C C周围的对称属性，绿色实线显示两侧必须匹配的区域。红色实线表示两侧可能不匹配的区域。虚线绿线表示穿过中心的区域。

  很明显，由两条实线绿线表示的区域中的两个子串必须完全匹配。中心区域（由绿色虚线表示）也必须是对称的。仔细注意 P [ i ′ ] P[i^\prime] P[i′]是7并且它一直延伸到回文的左边缘 （ L ） （L） （L）（由实线红线表示），它不再落在回文的对称性质之下。我们所知道的是 P [ i ] ≥ 5 P [i] ≥5 P[i]≥5，并且为了找到 P [ i ] P [i] P[i]的实数值，我们必须通过扩展经过右边缘 （ R ） （R） （R）来进行字符匹配。在这种情况下，由于 P [ 21 ] ≠ P [ 1 ] P [21]≠P [1] P[21]̸​=P[1]，我们得出结论 P [ i ] = 5 P [i] = 5 P[i]=5。

  让我们总结一下这个算法的关键部分如下：

if P[ i’ ] ≤ R – i,
	then P[ i ] ← P[ i’ ]
else P[ i ] ≥ P[ i’ ] // (我们必须扩展右边缘R来找到P[i]

  这里的时候博主观察到，但凡符合对称条件的回文串，其 P [ i ] P[i] P[i]的左端不能超过 P [ C ] P[C] P[C]的左端 R R R,而 P [ i ] P[i] P[i]到 R R R的左侧长度为 R − i R-i R−i。这就意味着，当 P [ i ′ ] ≤ R − i P[i^\prime]\le R-i P[i′]≤R−i的时候， P [ i ] = P [ i ′ ] P[i]=P[i^\prime] P[i]=P[i′]，这就满足了条件。但是如果 P [ i ′ ] &gt; R − i P[i^\prime]&gt; R-i P[i′]>R−i，这时候就不满足了。我们就得扩展右边缘，查看 L L L的左端和 R R R的右端相等不相等。如果不相等，则说明 P [ i ] = R − i P[i]=R-i P[i]=R−i。因为最大不能超过 R R R的另一边。即红色部分。但是如果两者确实能相等的时候，这时候中心就改变了。因为这种情况下，以 i i i为中心的字符串可达到原本 C C C的右端的后一位，同时左端达到了 C C C的左端的前一位，中心发生了移动，也就是说回文的中心发生了移动，我们可以把 C C C更新为 i i i，即这个回文的中心，并重新将 R R R扩展到新的回文右边缘上。

  总结起来就是，如果以 i i i为中心的回文确实扩展到 R R R，我们将 C C C更新为 i i i，（这个新回文的中心），并将 R R R扩展到新回文的右边缘。

算法复杂度分析
  • 时间复杂度： O ( n ) \mathcal{O}(n) O(n)，首先是插入特殊符号和更新数组 P [ i ] P[i] P[i]的每个元素并记录最大值
  • 空间复杂度： O ( n ) \mathcal{O}(n) O(n)，使用的都是一维数组。数量级在 O ( n ) \mathcal{O}(n) O(n)
算法代码
package Longest_Palindromic_Substring.five;
/**
 * 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
 */
public class Solution {
	
	public String longestPalindrome(String s) {
		if (s == null || s.length() < 1) return "";// 特殊情况判断
	    String T = preProcess(s);// 给字符串加#h号避免边界问题
	    int P[] = new int [T.length()];
	    int C=0,R=0,maxLen=0,centerIndex=0;
	    for(int i=1;i<T.length()-1;i++) {//尾元素不考虑
	    	 int i_mirror = 2*C-i; // equals to i' = C - (i-C)
	    	 P[i] = (R > i) ? Math.min(R-i, P[i_mirror]) : 0;
	    	 while (T.charAt(i+1+P[i])==T.charAt(i-1-P[i]))
	    	      P[i]++;// 试图扩大以i为中心的回文数据
	    	 //如果以i为中心的回文扩展到R，则根据扩展的回文调整中心
	    	 if(i+P[i] > R) {
	    		 C = i;
	    	     R = i + P[i];
	    	     if(P[i] > maxLen) {
	    	    	 maxLen = P[i];
	    	         centerIndex = i;
	    	     }
	    	 }
	    }
	    return s.substring((centerIndex - maxLen)/2, (centerIndex + maxLen)/2);
    }
	
	
	/**
	 * ^和$符号是附加到首位的标记，以避免边界检查
	 * 例如, S = "abba", T = "^#a#b#b#a#$".
	 */
	private String preProcess(String s) {
		StringBuilder s1 = new StringBuilder("^"); 
		for(int i=0;i<s.length();i++) {
			s1.append("#"+s.charAt(i));
		}
		s1.append("#$");
		return s1.toString();
	}


	public static void main(String[] args) {
		Solution n1 = new Solution();
		System.out.println(n1.longestPalindrome("babad"));// bab, aba
		System.out.println(n1.longestPalindrome("cbbd"));// bb
		System.out.println(n1.longestPalindrome("abcdf"));//a,b,c,d,f
		System.out.println(n1.longestPalindrome("a"));
		System.out.println(n1.longestPalindrome("bb"));
		System.out.println(n1.longestPalindrome("cccc"));
		System.out.println(n1.longestPalindrome("abacab"));// "bacab"*/
		System.out.println(n1.longestPalindrome("abcdbbfcba"));// "bb"
		System.out.println(n1.longestPalindrome("qrrohydrmbvtuwstgkobyzjjtdtjroq"));//jtdtj
	}
	
}

扩展的几种算法解决该问题

  Apostolico提出了一个算法，可以线性时间求出在线性时间内在输入串内的任何地方找到所有最大回文子串。该文可以在这里下载，Parallel detection of all palindromes in a string。

  Dan Gusfield提出了一个回文串算法，据说也是线性时间，在这里下载，Algorithms on Strings, Trees and Sequences，文章197~199页有显示，

  下面是部分截图，有兴趣的人可以试试。是后缀树的算法之一，该算法利用了字符串的通用后缀树及其反向实现。

YuYunTan
关注
  • 4
    点赞
  • 踩
  • 3
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 2
    评论
专栏目录
leetcode刷题——5.寻找最长回文字串
weixin_42846216的博客
05-21 314
寻找最长回文字串 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。 示例 1： 输入: "babad" 输出: "bab" 注意: "aba" 也是一个有效答案。 方法一：中心扩展法， 例如：baab中aa为回文子串，用p[i,j]表示，那s[i-1]==s[j+1],所以p[i-1,j+1]也为回文字串，中心扩展法考虑奇数串，偶数串，所以要判断两部分。 代码如下： class Solution { public: //确定回文字串左右端点的位置 //param
最大对称字符串的算法
12-26
算法一：O(n^3) 判断字串是否对称是从外到里， O(n) 代码如下:#include <stdio>#include <string> /* *判断起始指针，到结束指针的字符串是否对称 */int IsSymmetrical(char* pBegin, char* pEnd){    if(pBegin == NULL || pEnd == NULL || pBegin > pEnd)    return 0;     while(pBegin < pEnd)    {    if(*pBegin != *pEnd)        return 0;    pBegin++;  
leetcode答案-Longest-Palindromic-Substring:最长回文子串
06-30
leetcode 答案 Longest-Palindromic-Substring(最长回文子串) 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。 Sample 1 输入: "babad" 输出: "bab" 注意: "aba" 也是一个有效答案。 Sample 2 输入: "cbbd" 输出: "bb" 来源： 力扣（LeetCode） 链接：
寻找最长回文字符串扩展及优化
花明的博客
03-28 215
中心扩展法 从字符串中间向两边扩散寻找最长的回文字符串。分为两种情况字符串长度位奇数和偶数，比如 aba奇数,从下标为1处开始向两边寻找，可以找到最大回文；abba偶数从下标为1和2开始寻找，可以找到最大回文。 代码实现： public class Main{ // 输出最后一个最大的回文串 private static List<String> getLargeLength(St...
数组：查找最长回文串（1）
Greenland_coco的博客
11-08 969
方法：分奇数偶数从中心扩散 困难在于计算总数与每个比较的地方都只考虑数字。 任务描述 本关任务：编写一个程序，寻找一篇英文文章中最长的回文字符串。回文字符串是具有回文特性的字符串：即该字符串从左向右读，与从右向左读都一样。 编程要求 根据提示，在右侧编辑器补充代码，用户输入的文章不会超过10000字符。这个文件可能一行或多行，但是每行都不超过80个字符（不包括最后的换行符）。在寻找回文时只考虑字母 ‘A’ - ‘Z’ 和 ‘a’ - ‘z’ ，忽略其他字符（例如：标点符号，空格等）。输出的第一行应
回文串总结
qq_43344375的博客
09-04 80
LeetCode回文串系列一、动态规划1.模板：最长回文子串1）题目2）思路3）做法2.分割回文串1）题目2）思路3）做法3.分割回文串II1）题目2）思路3）做法 一、动态规划 1.模板：最长回文子串 1）题目 给你一个字符串 s，找到 s 中最长的回文子串。 2）思路 动归：处理出i到j是否是回文串的数组，更新记录最长的回文子串长度。时间复杂度恒为n方。 中心扩展：以每个字符为中心进行扩展回文字符串，时间复杂度最坏为n方，最好为n。 3）做法 动归做法 class Solution { publ
空字符串 - 最长回文子串
既然选择了远方 便只顾风雨兼程 - 永强
03-18 772
空字符串 - 最长回文子串 1. 空字符串 字符串常量的书写方式是用一对双引号包围一串字符，如下所示： “Hello” “\aWarning!\a” “Line 1\nLine2” “” 字符串常量 (不像字符常量) 可以是空的。即使是空字符串，依然存在作为终止符的 NUL 宇节。 literal [ˈlɪtərəl]：adj. 文字的，逐字的，无夸张的 string [strɪŋ]：n. 线，...
查找回文字符串
weixin_51222289的博客
11-11 3176
编写一个程序，寻找一篇英文文章中最长的回文字符串。 回文字符串是具有回文特性的字符串：即该字符串从左向右读，与从右向左读都一样。 输入文件不会超过500字符。这个文件可能一行或多行，但是每行都不超过80个字符（不包括最后的换行符）。在寻找回文时只考虑字母 ‘A’ - ‘Z’ 和 ‘a’ - ‘z’ ，忽略其他字符（例如：标点符号，空格等）。 输出的第一行应该包括找到的最长的回文的长度。下一行或几行应该包括这个回文的原文（没有除去标点符号，空格等），把这个回文输出到一行或多行（如果回文中包括换行符）。如果有多
寻找最长回文字符串
笨笨的灰太狼的博客
05-11 551
定义： 回文字符串是将字符串逆序后和原字符串一样的字符串，就是正着读和反着读都一样的字符串。 基本思路： 给定一个字符串，寻找它的回文字符串，我的实现思路是使用回溯法，具体如下：首先选定一个点，使用两个变量left和right分别指向该点的左右两侧，如果left和right指向的字符串相等，那么left向左移动一位，right向右移动一位，继续判断，直到left和right不相等，此时left和right所组成的字符串就是回文字符串，判断回文字符串长度，如果大于result,就更换result的值，否则不更
最长回文字串
DiggerWang的博客
07-16 1273
求最长回文字符串是面试中的一道经典题目！给定一个字符串s，从中找出最长的回文字符串： 比如： s = "fggfsrtrsa" 返回 "srtrs"   解题思路： 其实最简单的可以用动态规划，时间复杂度为O(n^2)，这种解法就不加赘述了。我这里会介绍时间复杂度为O(n)的算法： Manacher算法： 首先用特定字符，比如"#"，去填充原来的字符串s： 这样做的...
如何找到字符串中的最长回文子串？
热门推荐
CSDN资讯
10-01 1万+
作者 |channingbreeze责编 | 胡巍巍小史是一个应届生，虽然学的是电子专业，但是自己业余时间看了很多互联网与编程方面的书，一心想进BAT互联网公司。可是努...
LeetCode5 Longest Palindromic Substring
01-09
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000. Java AC 版本
最大公共字符串leetcode-longest-palindromic-substring:查找字符串中最长的回文子串
07-01
最长回文子串 给定一个字符串 s，找出 s 中最长的回文子串。 您可以假设 s 的最大长度为 1000。 Example 1: Input: "babad" Output: "bab" Note: "aba" is also a valid answer. Example 2: Input: "cbbd" Output: ...
最大公共字符串leetcode-longest-palindromic-substring:给定一个字符串s，找出s中最长的回文子串。你可以假
07-01
最长回文子串 给定一个字符串 s，找出 s 中最长的回文子串。 您可以假设 s 的最大长度为 1000。 示例 1： Input: "babad" Output: "bab" Note: "aba" is also a valid answer. 示例 2： Input: "cbbd" Output: "bb" ...
leetcode题库-LeetCode:力码
06-29
最长回文子串 Longest Palindromic Substring.cpp 7 整数反转 Reverse Integer.cpp 9 回文数 Palindrome Number.cpp 12 整数转罗马数字 Integer to Roman.cpp 13 罗马数字转整数 Roman to Integer.cpp 15 三数之和 3...
QLExpression学习使用教程
YuYunTan的专栏
09-26 1万+
文章目录QLExpress简介支持特性Maven引入例子github源码图分解提示例子初次使用Runner执行器设置执行器执行命令的设置支持普通的Java语法执行运算符支持运算符分类示例部分运算符列举样例使用表达式样例三目运算符样例数组定义Java对象使用数组遍历map遍历定义函数示例预定义装载函数定义操作符中文操作符替换二元操作符自定义自定义操作符需注意多元操作符操作符的使用操作符定义addOp...
三台centOS7虚拟机搭建Kubernetes集群【包括Docker安装】的图文详细教程
YuYunTan的专栏
09-27 5186
文章目录Docker安装设置Docker存储库安装所需的包（可选）启用夜间或测试存储库。安装Docke ENGINE - COMMUNITY安装docker18.09.7启动Docker验证是否安装成功查看版本是否正确设置开启启动Docker配置docker启动参数重启docker测试从Docker Hub pull下镜像K8S集群搭建关闭交换空间配置iptable管理ipv4/6请求安装kube...
DFS深度优先算法java算法
YuYunTan的专栏
11-24 3387
 我学习算法，按照老师给的算法弄的…… 完成时间2014年11月24日
矩阵连乘问题java版
YuYunTan的专栏
12-08 3024
/** * * @author YuYunTan(谭淇蔚) *定义数组P[i] *p[i]的含义有两层 *指的是： *1. 第i个矩阵的列 *2. 第i+1个矩阵的行 * *思路： *步骤： *划分阶段（子问题）并刻画 *将原问题划分成两个子问题。如果原问题获得最优值。则子问题的应该也是最优的。 *将矩阵连乘积A1A2A3A4简记为A(1:n) *设最优计算次序在矩阵
leetcode最长回文子串
最新发布
07-27
- *3* [LeetCode 第5题：最长回文子串（Python3解法）](https://blog.csdn.net/weixin_43490422/article/details/126479629)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

YuYunTan

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值