RSA公钥密码算法的原理及实现(二)

最新推荐文章于 2024-04-11 11:33:49 发布

A00553344

最新推荐文章于 2024-04-11 11:33:49 发布

阅读量2w

点赞数 1

文章标签：算法加密测试 pascal c 解密

本文链接：https://blog.csdn.net/a00553344/article/details/3747434

版权

RSA公钥密码算法的原理请看：

http://blog.csdn.net/A00553344/archive/2009/01/07/3730194.aspx

下面主要论述RSA公钥密码算法的具体实现。

预备知识

RSA公钥密码算法需要多精度算术（通常被称为"大数"数学）。RSA需要很大的整数来抵御已知的密码攻击。比如，一个典型的RSA模数至少大于10³⁰⁹，而现代编程语言C,JAVA,PASCAL等仅支持相对较小且单精度的整数。为了解决这个问题，我们引入了多精度整数。

n为多精度整数可表示为x=(x_n-1,...,x₁,x₀)_β,它表示整数x=∑x_iβⁱ。数组中的x表示以β为基的每一位的值。比如，x=(1,2,3)10表示整数1*10²+2*10¹+3*10⁰=123。为了方便编程，我们引入一个复合结构mp_int来表示多精度数，它包含其所表示的整数的每一位值，以及操作这些数据所需的辅助数据。

mp_int，它是一个结构。

C语言结构描述如下：

typedef struct{

int used,alloc,sign;

mp_digit *dp;

} mp_int;

Object Pascal语言描述如下：

    mp_int    = record                    {MP integer number           }
                dp     : PDigitArray; {pointer to mp_digit array      }
                alloc   : word;                {allocated digits in pdigits }
                used   : word;                {used digits in pdigits      }
                sign    : word;               {sign: MP_ZPOS or MP_NEG     }
    end;

这里的mp_digit是单精度整数。在C语言里，它有可能是unsigned long; 在PASCAL里，它有可能是Cadinal;它其实也代表了多精度数的基β。比如，unsigned long为32位，假如我们取其低30位来表示多精度数的每一位。那么这个多精度数的基β=2³⁰。当dp数组存放了三个数；dp[0]=1,dp[1]=2,dp[2]=3,那么这个多精度数就是x=dp[2]*β²+dp[1]*β¹+dp[0]*β⁰=3*(2³⁰)²+2*(2³⁰)¹+1*(2³⁰)⁰。

成员定义如下：

used参数表示数组dp用多少位数来表示一个指定整数。used必须是正数（或0），并且不能超过alloc的值。
alloc参数表示数组在增加大小之前可用的数据位。当used大于alloc数时，所有算法都会自动增加数组的大小，以适应结果的精度。
dp表示动态分配的代表指定多精度整数的数组。不足的位（alloc - used）全部填0。数组中的数据按LSB在先的顺序存储。
sign参数表示数字为0(正)或非0(负)。

一、n的长度。

RSA的安全性完全依赖于分解大数的难度。从技术上说这是不正确的，这只是一种推测。从数学上从未证明过需要分解n才能从c和e中计算出m。用一种完全不同的方法来对RSA进行密码分析还只是一种想象。如果这种新方法能让密码分析者推算出d的话，它也可以作为分解大数的一种新方法。从目前看，分解n是最显而易见的攻击方法。攻击者手里有公开密钥e和n，要想找到解密密钥，他们就必须分解n。

对大数进行因式分解是困难的。不幸的是，对算法设计者来说它正变得越来越容易。更加糟糕的是，它比数学家们所希望的还要快。1977年，Ron Rivest说过分解一个125位(十进制)的数据需要40 * 10¹⁵年。可是，一个129位的数已经在1994年被成功分解。大数因式分解最近的记录是RSA200，一个200位的非特殊数字，在2005年计算机花了18个月时间才把它分解成两个素数。而目前一个国际组织则打破了这个保持了2年之久的记录，3月6日来自3个机构的计算机集群（EPFL，波恩大学，日本电话电报公司）在经过11个月的计算后终于成功的把一个有名的很难分解的大数—2^1039 - 1 —一个307位的数字—分解出两个素数因子。

基于目前的因式分解的发展情况，下面给出了一些公开密钥长度的推荐值(即n的位数,二进制)。

年度	对于个人	对于公司	对于政府
1995	768	1280	1536
2000	1024	1280	1536
2005	1280	1536	2048
2010	1280	1536	2048
2015	1536	2048	2048

在实际应用中，目前RSA-1024仍然是安全的，但新的应用程序真的应该使用至少RSA-1536或更高。业界的许多人设置最小为2048位的密钥，来避免将来可能的实际进展所带来的安全危机。

二、p,q的选择。

因为任何潜在的破解方都可能知道n=pq的值，为了防止通过穷举方法来发现p和q, p和q这两个素数的选择必须从足够大的集合中进行选取。另一方面，用来找到大素数的方法必须相当有效。

现在还没有产生任意的大素数的有用技术，因此解决这个问题需要其他方法。通常使用的过程是随机选取一个需要的数量级的奇数并检验这个数是否是素数。如果不是，选取后续的随机数直到找到了通过检验的素数为止。

检验素数方面已经出现了很多方法。几乎所有的检验方法都是概率性的，也就是说，这个检验只是确定一个给定的整数可能是素数。虽然缺乏完全的确定性，但是这些检验在运行时可以按照需要做到使得概率尽可能接近1。

下面介绍一下素性检验几种主要方法。为了讨论方便，我们用n表示要进行素性检验的整数。

1. 试除法(Trial Division)。

试除法是指试图最终用一个小素数除尽一个候选整数。将n除以q,q为素数且,如果n可被整除，则显然n不是素数。此测试可实际证明一个整数是否是素数。不过，n增大时其所需的时间会大大增加。为了减少计算的时间，我们可以不用每个素数去除n，而是改用一组更小、更易于管理的素数。通过对小于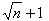的素数的一个子集执行试除法。该算法无法确定n是否是素数，但是它可以证明n是否不是素数。

这个测试的好处在于除以小的值的试除法相当有效快速。常用于其他素性测试算法前的预筛选工作。剔除掉大部分的非素数。

算法描述：

-------------------------------------------------------------------

输入：mp_int a

返回：如果n可由小素数整除，则返回真,否则返回假。

-------------------------------------------------------------------

<1>. 预先生产一个素数表，一般选择[0x0000H, 0xFFFFH]范围内的素数组成一个素数表Prime_Table,它所包含的素数个数为PRIME_SIZE。

<2>. 将Prime_Table内的素数逐个执行

<1.1>. d ← n(mod Prime_table[i]) ; 0≤i<PRIME_SIZE

<1.2>. 如果d=0,则返回真; 否则返回假.

<3>. 结束.

--------------------------------------------------------------------

常用的Prime_table如下：

const mp_digit prime_table[] = {
0x0002, 0x0003, 0x0005, 0x0007, 0x000B, 0x000D, 0x0011, 0x0013,
0x0017, 0x001D, 0x001F, 0x0025, 0x0029, 0x002B, 0x002F, 0x0035,
0x003B, 0x003D, 0x0043, 0x0047, 0x0049, 0x004F, 0x0053, 0x0059,
0x0061, 0x0065, 0x0067, 0x006B, 0x006D, 0x0071, 0x007F, 0x0083,
0x0089, 0x008B, 0x0095, 0x0097, 0x009D, 0x00A3, 0x00A7, 0x00AD,
0x00B3, 0x00B5, 0x00BF, 0x00C1, 0x00C5, 0x00C7, 0x00D3, 0x00DF,
0x00E3, 0x00E5, 0x00E9, 0x00EF, 0x00F1, 0x00FB, 0x0101, 0x0107,
0x010D, 0x010F, 0x0115, 0x0119, 0x011B, 0x0125, 0x0133, 0x0137,

0x0139, 0x013D, 0x014B, 0x0151, 0x015B, 0x015D, 0x0161, 0x0167,
0x016F, 0x0175, 0x017B, 0x017F, 0x0185, 0x018D, 0x0191, 0x0199,
0x01A3, 0x01A5, 0x01AF, 0x01B1, 0x01B7, 0x01BB, 0x01C1, 0x01C9,
0x01CD, 0x01CF, 0x01D3, 0x01DF, 0x01E7, 0x01EB, 0x01F3, 0x01F7,
0x01FD, 0x0209, 0x020B, 0x021D, 0x0223, 0x022D, 0x0233, 0x0239,
0x023B, 0x0241, 0x024B, 0x0251, 0x0257, 0x0259, 0x025F, 0x0265,
0x0269, 0x026B, 0x0277, 0x0281, 0x0283, 0x0287, 0x028D, 0x0293,
0x0295, 0x02A1, 0x02A5, 0x02AB, 0x02B3, 0x02BD, 0x02C5, 0x02CF,

0x02D7, 0x02DD, 0x02E3, 0x02E7, 0x02EF, 0x02F5, 0x02F9, 0x0301,
0x0305, 0x0313, 0x031D, 0x0329, 0x032B, 0x0335, 0x0337, 0x033B,
0x033D, 0x0347, 0x0355, 0x0359, 0x035B, 0x035F, 0x036D, 0x0371,
0x0373, 0x0377, 0x038B, 0x038F, 0x0397, 0x03A1, 0x03A9, 0x03AD,
0x03B3, 0x03B9, 0x03C7, 0x03CB, 0x03D1, 0x03D7, 0x03DF, 0x03E5,
0x03F1, 0x03F5, 0x03FB, 0x03FD, 0x0407, 0x0409, 0x040F, 0x0419,
0x041B, 0x0425, 0x0427, 0x042D, 0x043F, 0x0443, 0x0445, 0x0449,
0x044F, 0x0455, 0x045D, 0x0463, 0x0469, 0x047F, 0x0481, 0x048B,

0x0493, 0x049D, 0x04A3, 0x04A9, 0x04B1, 0x04BD, 0x04C1, 0x04C7,
0x04CD, 0x04CF, 0x04D5, 0x04E1, 0x04EB, 0x04FD, 0x04FF, 0x0503,
0x0509, 0x050B, 0x0511, 0x0515, 0x0517, 0x051B, 0x0527, 0x0529,
0x052F, 0x0551, 0x0557, 0x055D, 0x0565, 0x0577, 0x0581, 0x058F,
0x0593, 0x0595, 0x0599, 0x059F, 0x05A7, 0x05AB, 0x05AD, 0x05B3,
0x05BF, 0x05C9, 0x05CB, 0x05CF, 0x05D1, 0x05D5, 0x05DB, 0x05E7,
0x05F3, 0x05FB, 0x0607, 0x060D, 0x0611, 0x0617, 0x061F, 0x0623,
0x062B, 0x062F, 0x063D, 0x0641, 0x0647, 0x0649, 0x064D, 0x0653
};

除了事先预备好素数表之外，也可以直接判断是否为小于0x0FFFH之内的素数，然后被n整除来试除。

2. 费马(Fermat)测试。

费马测试可能是最早的一种成功的测试方法。它基于费马小定理：如果n确定是素数，则对于所有0<a<n有aⁿ≡a(mod n)。如果n不是素数，则可能存在aⁿ≠a(mod n)。所以，如果一个非素数n满足0<a<n有aⁿ≡a(mod n)。我们称之为伪素数。幸运的是，当n增大的时伪素数非常的少见。

算法描述如下：

---------------------------------------------------------------------

给定奇整数n≥5和安全参数t,

<1>. 随机选取整数a,2≤a≤n-2。

<2>. 计算g=gcd(a,n),如果g≠1,则n不为素数。

<3>. 计算r=aⁿ(mod n)，如果r≠a,则n不为素数。

<4>. 如果不为<2>,<3>的情况，则n可能为素数。

<5>. 上述过程重复t次。如果每次得到n可能为素数，则n为素数的概率为1-(1/2^t)。

---------------------------------------------------------------------

3.米勒-罗宾(Miller-Rabin)测试。

米勒-罗宾测试是另一种素数测试方法。它对错误的限制比费马测试更严格，尤其是当按顺序选择候选整数时。它的定义如下。

[定义]设n(≥3)是一个奇整数且n-1=2^sm，其中s≥0,m是一个奇整数。如果b^m≡1(mod n)或者b^m≡-1(mod n)或者有r(1≤r≤s-1)使b^{2^r}m≡-1(mod n),则称n通过以b为基的Miller-Rabin测试。

算法描述如下：

----------------------------------------------------------------------

给定奇整数n(≥3,且n-1=2^sm,其中s≥0,m是一个奇整数)和安全参数t。

<1>. 随机选取整数b,1≤b≤n-1。

<2>. r ← 0。

<3>. z=b^m(mod n)。

<4>. 如果z=1或z=n-1,则n可能是素数；转<10>。

<5>. 如果r=s-1,则n是合数；转<10>。

<6>. r=r+1。

<7>. z=z²(mod n)。

<8>. 如果z=n-1,则n可能是素数；转<10>.

<9>. 转<5>。

<10>. 上述过程重复t次。如果每次得到n可能为素数，则n为素数的概率为1-(1/4^t)。

---------------------------------------------------------------------------

4.Baillie-PSW 素性测试

BPSW（Baillie-PSW)测试是一个基于其他素性测试的组合测试。

测试步骤如下：

<1>. 给定奇整数n(≥3)。

<2>. 先进行试除法看n是否有小素数因子。如果有，则n不是素数。

<3>. 然后进行基于2的Miller-Rabin素性测试。

<4>. 最后进行Lucas-Selfridge素性测试。

现在我们知道了几种大素数的检测方法。通过它们及选定的n的位数，我们可以获取需要的大素数p和q。但是为了避免选择容易分解的数值n，算法的发明者建议对p和q施加如下的限制：

p和q的长度应只差几个数字。
(p-1)和(q-1)都应该包含大的素因子。
gcd(p-1,q-1)应该很小。

三、e的选择

为了提高RSA的加密速度。最常用的三个e值是3,17和65537。（X.509中建议采用65537，PEM中建议采用3，PKCS#1中建议采用3或65537）。

四、软件加速

假如你已经保存了p和q值，及诸如d mod(p-1), d mod(q-1), q^-1 mod p这类数，那么运用中国剩余定理(CRT)就能使私钥的运算速度加快。

五、RSA实现过程

1. 密钥生成

RSA的密钥生成从概念上来看是一个简单的过程，但它在实际中并不简单，尤其是对于寻求速度的实现。

----------------------------------------------------------------------------------------------------------------------------------------

输入：

e: 公开的指数。

n: 需要的模数的位长。

输出：

n: 公开的模数。

d: 私有的指数。

<1>. 选择一个随机素数p,长度为n/2位，使得gcd(p-1,e)=1

<2>. 选择一个随机素数q,长度为n/2位，使得gcd(q-1,e)=1

<3>. 令n=pq

<4>. 计算d=e^-1 mod (p-1)(q-1)

<5>. 返回n,d

-----------------------------------------------------------------------------------------------------------------------------------------

2.RSA变换

因为RSA算法中加密的是一个整数。而实际情况中的是消息（解释为一个八位位组的数组）。所以在加密前，需要把消息转换成一个整数。具体的信息在下面的PKCS#1标准中说明。

3.PKCS#1

PKCS#1（www.rsasecurity.com/rsalabs/node.asp?id=2125）是一个RSA标准，它指定了怎样使用RSA变换来作为一个陷门原型正确地对消息进行加密和签名。PKCS#1很明显地使用ASN.1原型并且需要一个密码散列函数。PKCS#1标准分成4个部分。

<1>. PKCS#1数据转换

PKCS#1指定了两个函数，OS2IP和I2OSP，它们分别执行八位位组串到整数之间的转换。它们用来描述一个八位位组（字节）串是怎么样转换成一个用于RSA变换处理的整数的。

OS2IP函数把一个八位位组串映射为一个整数，这是通过用big-endian的方式装载八位位组来完成的。即第一个字节是最有效的。I2OSP执行相反的操作而不需要填充。也就是说，如果输入的八位位组串有头零八位位组，I2OSP输出不影响这一点。

<2>. PKCS#1密码原型

PKCS#1指定了4种密码原型，但是从技术上来看，只有两种唯一的原型。RSAEP原型通过计算整数的e次方然后再模n来执行RSA的变换。RSADP原型执行一种相似的操作，不同的是它使用指数d。除了头零和输入除模数n之外，RSADP是RSAEP的逆。这个标准指定了RSADP怎么样使用中国剩余定理（CRT）来加速运算。

这个标准也指定了RSASP1和RSAVP1，分别对应RSADP和RSAEP。这些原型用于签名算法中。

<3>. PKCS#1加密机制

RSA的加密机制有两种方案一个是RSAES-OAEP，另一个RSAES-PKCS1-v1_5。PKCS#1推荐在新的应用中使用RSAES-OAEP，保留RSAES-PKCS#1-v1_5跟老的应用兼容。它们两的区别仅仅在于加密前编码的方式不同。而加密前的编码是为了提供了抵抗各种活动的敌对攻击的安全机制。解密首先是应用RSADP，然后是OAEP或PKCS1-v1_5的逆操作。相比于OAEP，PKCS1-v1_5的编码方式相对比较简单。我们这里介绍一下RSAES-PCKS1-v1_5的步骤。

------------------------------------------------------------------------------------------------

输入：

（n,e）：公钥。记n的长度(以八位位组表示，也就是我们说的Byte)为k。

M：需要被加密的信息。它的长度(以八位位组表示)为mLen。

输出：

C：加密后的密文。长度为k。

步骤：

1.长度检查。如果mLen > k - 11, 则输出"被加密的信息长度太长!"的错误信息。

2.开始PKCS1-v1_5编码：

- 产生一个长度为k-mLen-3的八位位组数组PS,其内容为随机产生的非零八位位组。PS的长度至少为8个八位位组。
- 以下面的次序连接成一个编码串EM。

EM = 0x00 || 0x02 || PS || 0x00 || M

3.开始RSA加密：

- 将编码串EM转换成一个整数值m。

m=OS2IP(EM)

- 利用公钥对m进行加密，输出加密后的一个整数值c。

c=RSAEP((n,e),m)

- 将加密的输出c转换成长度为k的加密后的八位位组串C。

C=I2OSP(c,k)

4.输出C。

------------------------------------------------------------------------------------------------

注意：PKCS1-v1_5的编码方式对能够加密的明文大小做了限制。明文的最大长度是k-11。比如，我们选择RSA-1024来加密，那么k=1024/8=128, mLen = k - 11 = 117。也就是说PCKS1-v1_5的负载限制是117个八位位组（也可以说是117个ASCII字符）。通常，这不算什么大问题。因为RSA一般都用在混合加密方式中,加密的明文长度一般都比较小。

<4>. PKCS#1签名机制

跟加密机制一样，PKCS#1的签名机制也有种方案：RSASSA-PSS和RSASSA-PKCS1-v1_5。同样，推荐RSASSA-PSS用于新的应用而RSASSA-PKCS1-v1_5用于兼容老的应用。这里也只介绍一下相对简单一些的RSASSA-PKCS1-v1_5的步骤。

------------------------------------------------------------------------------------------------

输入：

（n,d）：私钥。

M：被签名的信息，八位位组数组。

输出：

S：签名。长度为k的八位位组数组。k为n的长度(以八位位组表示，也就是我们说的Byte)。

步骤：

1.对信息M采用EMSA-PKCS1-v1_5编码，输出长度为k的八位位组数组EM。

2.RSA签名。

- 将EM转换成一个整数值m。

m=OS2IP(EM)

- 用RSASP1对m进行签名，输出一个整数值s。

s=RSASP1((n,d),m)

- 将s转换成长度为k的八位位组数组S。

S=I2OSP(s,k)

3.输出签名S。

------------------------------------------------------------------------------------------------

EMSA-PKCS1-v1_5编码步骤如下：

------------------------------------------------------------------------------------------------

输入：

M：需要编码的信息。

emLen：信息的长度。必须满足emLen >= tLen + 11。 tLen在下面解释。

输出：

EM：长度为emLen的编码后的八位位组数组。

步骤：

1. 对输入的信息M计算一个散列值H。H=Hash(M)。这里的Hash函数由自己选择。

2. 根据选择的Hash函数及计算好的散列值H来获取一个编码串T。它其实是一个结构的DigestInfo的ASN.1编码。DigestInfo结构定义为：

DigestInfo ::= SEQUENCE{

digestAlgorithm AlgorithmIdentifier,

digest OCTET STRING

}

digestAlgorithm存放所选Hash函数的OID。digest存放用这个Hash函数对信息M计算后的散列值。下面是一些常用Hash函数的T值：

- MD2: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 02 05 00 04 10 || H
- MD5: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 05 05 00 04 10 || H
- SHA-1: (0x)30 21 30 09 06 05 2b 0e 03 02 1a 05 00 04 14 || H
- SHA-256:(0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 01 05 00 04 20 || H
- SHA-384:(0x)30 41 30 0d 06 09 60 86 48 01 65 03 04 02 02 05 00 04 30 || H
- SHA-512: (0x)30 51 30 0d 06 09 60 86 48 01 65 03 04 02 03 05 00 04 40 || H.

这个编码串T的长度（以八位位组表示）就是上边提到的tLen 。

3.如果emLen<tLen + 11的话，则输出错误信息"编码信息长度不够"。

4.产生一个长度为emLen-tLen-3的八位位组数组PS。其值均填充为0xff。PS的长度至少要为8个八位位组。

5.按下面的顺序编码，获得EM：

EM = 0x00||0x01||PS||0x00||T

6.输出EM。

------------------------------------------------------------------------------------------------

注：ASN.1编码的信息可以看我的另一篇文章http://blog.csdn.net/A00553344/archive/2009/01/04/3703903.aspx

六、举例

现在分三步来具体实现这个过程。

第一步：生成公钥和私钥。

根据选择的n的位数，随机产生n/2位的p和q两个大素数。然后选择e的取值和私钥的方式(d,n)或带有CRT系数的PrivateKey.(注：带有CRT系数的私钥可以加快解密的速度)

这里，取n=1024位；e=3；私钥方式为普通的(d,n),计算获得：

公钥对：

e=3
n=628d3f9173aae53ece12cdef548a0169c0c6045c886ccee6a643cb2996b298d6b8e7b1d2989ff4a8b840ca396e69e4821f83e4d0655240c9d5aa16f8cbcefd69f834420379b3584c4076bfe8dfb823117cac5f9f237a3d900c8121199ebb708a84adba6a0ce244722680dc14518aa909dffb7b8db681dbe7837d557566be024b

私钥对：

d=106cdfed93472635225877a7e36c5591a02100ba16bccd26710b4c86ee7319791ed1484dc41aa8c6c96021b43d11a615afeb50cd66386021a39c5929774d2a3c1e9c6e4feef48413d64a0682f6e39b6e87ccf569e80d6510bdb0f7ae3c241ea7982282a831e975d2ee50cceca8a826e31553928f3ebf613678a6b2da1ed2273f
n=628d3f9173aae53ece12cdef548a0169c0c6045c886ccee6a643cb2996b298d6b8e7b1d2989ff4a8b840ca396e69e4821f83e4d0655240c9d5aa16f8cbcefd69f834420379b3584c4076bfe8dfb823117cac5f9f237a3d900c8121199ebb708a84adba6a0ce244722680dc14518aa909dffb7b8db681dbe7837d557566be024b

第二步：加密明文。

我们选择明文信息为： "hello world!"

加密后密文表示为16进制：

9ECD79E6CA15AB4AA777F53C532E26234BA9D134E9FF5EC5EB8FF9E96428ABBA89C6567F13995F72F87FEF79EE7AF1E9FDCFEBBD1BF9

F0ECB5B2BF81A97F5E3097E1EB94F01EE233BFB783F4B931B8C647842D9AFDA3944B185D8EBBD1BEBE4C993B383196B989675D99D8AE

9CD227EEE6F5758A6A711434BBE05D5D1B64

第三步：解密密文。

解密后恢复出来的信息为"hello world!"

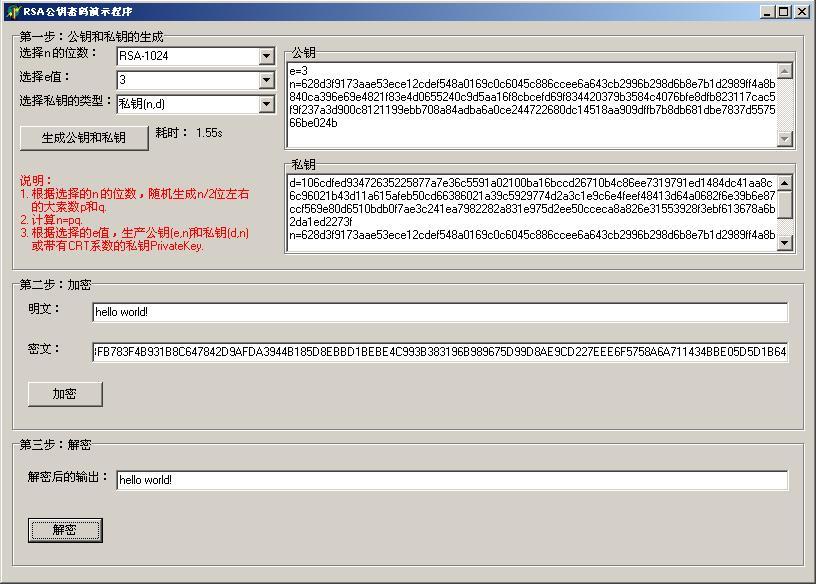
下面是程序的截图:

A00553344

关注

1
点赞
踩
21

收藏

觉得还不错? 一键收藏
6
评论
RSA公钥密码算法的原理及实现(二)

RSA公钥密码算法的原理请看：http://blog.csdn.net/A00553344/archive/2009/01/07/3730194.aspx下面主要论述RSA公钥密码算法的具体实现。预备知识 RSA公钥密码算法需要多精度算术（通常被称为"大数"数学）。RSA需要很大的整数来抵御已知的密码攻击。比如，一个典型的RSA模数至少大于10309，而现代编程语言
复制链接

扫一扫