【题解】Paint Color Aizu - 0531(经典问题离散化) ⭐⭐⭐

最新推荐文章于 2023-12-27 17:11:49 发布

原创最新推荐文章于 2023-12-27 17:11:49 发布 · 562 阅读

0 ·

CC 4.0 BY-SA版权

思维算法专栏收录该内容

61 篇文章

订阅专栏

本文介绍了一个计算长方形三合板上未被护板遮挡区域的涂色数量的算法。通过离散化处理和搜索算法，解决了数据量大的情况下如何高效计算的问题。

Paint Color Aizu - 0531

为了宣传信息竞赛，要在长方形的三合板上喷油漆来制作招牌。三合板上不需要涂色的部分预先贴好了护板。被护板隔开的区域要涂上不同的颜色，比如上图就应该涂上5种颜色。
请编写一个程序计算涂色数量，输入数据中，保证看板不会被护板全部遮住，并且护板的边一定是水平或垂直的。

Input

第一个数是宽w（1 ≤ w ≤ 1000000），第二个数是高h（1 ≤ h ≤ 1000000）。
第二行是护板的数量n（1 ≤ n ≤ 1000），接着n行是每个护板的左下角坐标 (x1 , y1 )和右上角坐标 (x2 , y2 )，用空格隔开： x1 , y1 , x2 , y2 (0 ≤ x1< x2 ≤ w, 0 ≤ y1 < y2 ≤ h 都是整数)
招牌的坐标系如下，左下角是 (0, 0) ，右上角是(w, h) ，测试集中的30%都满足w ≤ 100, h ≤ 100, n ≤ 100。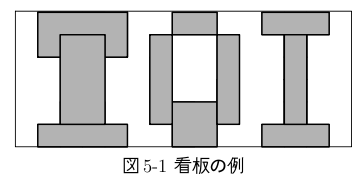在这里插入图片描述

Output

颜色的数量

Examples

Sample Input
15 6
10
1 4 5 6
2 1 4 5
1 0 5 1
6 1 7 5
7 5 9 6
7 0 9 2
9 1 10 5
11 0 14 1
12 1 13 5
11 5 14 6
0 0

Sample Output
5

Hint

题意:

题解:

白书例题, 其实就是求图中区域的个数就好了, 首先考虑直接搜索就能写, 但是由于数据过大, 可能会超时
这时我们要对数据进行离散化处理

经验小结:

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define ms(x, n) memset(x,n,sizeof(x));
typedef  long long LL;
const int inf = 1<<30;
const LL maxn = 1010;

int W, H, N;
int X1[maxn], X2[maxn], Y1[maxn], Y2[maxn];
bool fld[maxn * 3][maxn * 3];
int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
int compress(int *x1, int *x2, int w){
    vector<int> xs;
    for(int i = 0; i < N; i++){
        for(int d = -1; d <= 1; d++){
            int tx1= x1[i] + d, tx2 = x2[i] + d;
            if(0 <= tx1 && tx1 < w) xs.push_back(tx1);
            if(0 <= tx2 && tx2 < w) xs.push_back(tx2);
        }
    }
    sort(xs.begin(), xs.end());
    xs.erase(unique(xs.begin(), xs.end()), xs.end());
    for(int i = 0; i < N; i++){
        x1[i] = find(xs.begin(), xs.end(), x1[i]) - xs.begin();
        x2[i] = find(xs.begin(), xs.end(), x2[i]) - xs.begin();
    }
    return xs.size();
}
void solve(){
    W = compress(X1, X2, W);
    H = compress(Y1, Y2, H);
    ms(fld, 0);
    for(int i = 0; i < N; i++){
        for(int y = Y1[i]; y <= Y2[i]; y++){
            for(int x = X1[i]; x <= X2[i]; x++){
                fld[y][x] = true;
            }
        }
    }
    int ans = 0;
    for(int y = 0; y < H; y++){
        for(int x = 0; x < W; x++){
            if(fld[y][x]) continue;
            ans++;
            queue<pair<int, int> > que;
            que.push(make_pair(x, y));
            while(!que.empty()){
                int sx = que.front().first, sy = que.front().second;
                que.pop();
                for(int i = 0; i < 4; i++){
                    int tx = sx + dx[i], ty = sy + dy[i];
                    if(tx < 0 || W <= tx || ty < 0 || H <= ty) continue;
                    if(fld[ty][tx]) continue;
                    que.push(make_pair(tx, ty));
                    fld[ty][tx] = true;
                }
            }
        }
    }
    printf("%d\n", ans);
}
int main()
{
    while(cin >> W >> H, W || H){
        cin >> N;
        for(int i = 0; i < N; i++){
            cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i];
            X2[i]--, Y2[i]--;
        }
        solve();
    }
    return 0;
}