数据结构知识点总结

一、树

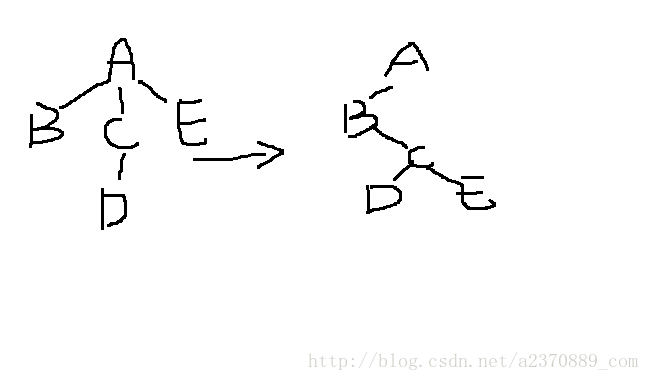
1、树（森林）和二叉树可以相互转化，规则是“左孩子右兄弟”，即当前节点的左孩子在由二叉树转化为树的过程中，左孩子还是当前节点的左孩子，而右节点会变成当前节点的兄弟。

2、设二叉树度为0的节点有N0个，度为2的节点为N2，则N2=N0+1

二、图

1、无向图的数据结构是邻接多重表，有向图的数据结构是十字链表。二者都可以使用邻接表

2、使得图从偏序到全序的遍历序列即拓扑排序，拓扑排序要求图是无环的。形成一个有序的拓扑序列的充要条件是图的邻接矩阵为三角矩阵。

3、使得无向图为连通图的，至少有V-1条边，而有向图为V条，即成环。

4、若要保证连通N个结点的无向图，则需要9个结点的完全图+本身，即C（9，2）+1

5、图的最小生成树算法：

（1）Prim和Kruskal算法都采用了优先队列作为数据结构。

（2）两种算法都不能用作有向图的最小生成树（或者应该叫做最小生成树形）

（3）从实现上来讲kruskal更简单一点。。。

（4）时间复杂度：Prim:Kruskal==ElogV:ElogE 空间复杂度：V:E

6、拓扑排序：

（1）要求：DAG有向无环图，权重为正，使用栈作为辅助存储的数据结构，即深度优先搜索得到的逆后序。

（2）时间复杂度：E+V 是无环图中的最优算法

7、Dijkstra算法

（0）时间复杂度：ElogV，使用斐波那契堆最好可以达到E+VlogV，在最坏情况下依然有较好的性能。

（1）和Prim算法十分相近，复杂度一样(采用邻接矩阵/邻接表的时候为N²，使用优先队列和斐波那契堆能到(m+n)logn）

。区别在于Prim算法是计算无向图的，Dijkstra是计算有向图的（当然无向图也能算，就每次添加边的时候邻接矩阵添加两个顶点即可）。 而Prim每次是加入离树最近的非树顶点，而Dijkstra是每次加入离起点最近的非树顶点。

（2）对于无环有向图，Dijkstra算法可以配合拓扑排序优化性能，即对拓扑序列的顶点都进行“放松”操作。可以在线性时间O(E+V)内完成。而且本变种算法可以处理权重为负的情况以及计算单点最长路径。同样的，因为是拓扑序列，所以不用marked[]标记是否访问过，每个顶点都只会被访问一次。

（3）和Kosaraju的比较：

相同点：都采用了拓扑序列作为访问顺序，都要取反（一个是反向图，一个是权重取相反数），时间复杂度 都是线性时间。

区别：一个是求无环加权有向图中的最长/短路径，一个是求有向图中的强连通分量

8、Bellman-Ford算法

1. 数据结构：采用队列（SPFA），一个Boolean型数组，防止重复加入队列，入队后置为true，出队后置为false
2. 时间复杂度：EV（每一轮中都会放松E条边，持续V轮，即将整个图每条边都放松），最好情况下和拓扑排序一样是E+V，适用领域广泛。
3. 解决问题：检测并判定负权重环是否存在，权重可正可负，有效解决最短路径问题，套汇问题：即寻找负权重环。
4. 当所有边放松V轮（即应该结束循环之后）之后，且仅当队列非空时，有向图中才存在负权重环。