直观理解Neural Tangent Kernel

直观理解Neural Tangent Kernel

本文是文章Some Intuition on the Neural Tangent Kernel的翻译整理.

一句话总结：NTK衡量的是，在使用SGD优化参数下，其对应的随机到样本$x^{\prime }$，在参数更新非常一小步$\eta$后，$f(x)$的变化。也就是：

$$k(x,x^{\prime })=\underset{\eta \to 0}{\lim }\frac{f\left(x,\theta +\eta \frac{d{f}_{\theta }(x^{\prime })}{d\theta }\right)-f(x,\theta )}{\eta }$$

热身

考虑最简单的函数$f(i)$，在每个点i都有一个不同的取值，这些取值可以用一个参数${\theta }_i=f(i)$来表示，如果我们初始化${\theta }_i=3i+2$，那么这个函数大概长这样:

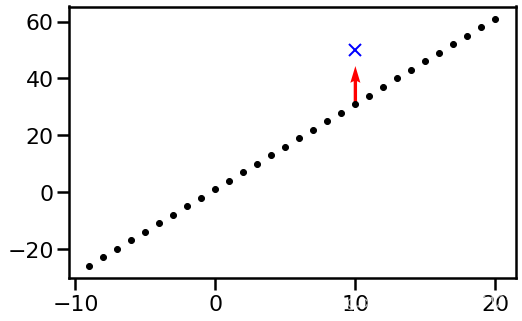
假设现在有一个样本是$(x,y)=(10,50)$，那么根据这个样本，我们需要对这个函数进行梯度更新，显然，这个样本只会影响$f(10)$这个点的参数${\theta }_{10}$，所以其他参数并不会发现变化，只会在10这个点变化，而这个变化如图上红色箭头所示。

显然，假设我们使用squared error loss，$L=(f(10;\theta )-50{)}^2$，并且设更新步长$\eta =0.1$，那么$\frac{\partial L}{\partial {\theta }_{10}}=\frac{\partial }{\partial {\theta }_{10}}({\theta }_{10}-50{)}^2=2(32-50)=-36$，显然为了让loss减少，于是${\theta }_{10}={\theta }_{10}-\eta \frac{\partial L}{\partial {\theta }_{10}}=32+0.1\ast 36=35.6$，我们发现$f(10)$这个点增加3.6

线性函数

刚才的例子只有一个参数发生变化，过于特殊，现在给一个线性函数的例子，设$f(x,\theta )={\theta }_{1}x+{\theta }_2$. 我们初始化参数为${\theta }_1=3,{\theta }_1=1$，这样，跟上面的例子差不多，不过这是一条直线，同样考虑样本点$(x,y)=(10,50)$，在该样本下，作一次梯度下降更新参数，

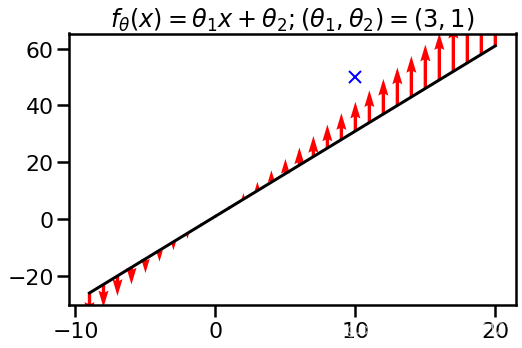
我们发现，所有x的取值都会发现变化，而我们关注的点$f(x)$也会离目标值更近了点。

Nerual tangent kernel

考虑某个点x，我们关心该函数在该点下的取值为$f_{\theta }(x)$，在SGD算法中，往往随机抽一个样本$x^{\prime }$，我们想要知道，在这个新样本下，更新一次参数$\theta$，$f(x)$会发生什么变化，而nerual tangent kernel$k(x,x^{\prime })$正是衡量这种变化的函数：

$$\eta {\tilde{k}}_{\theta }(x,x^{\prime })=f\left(x,\theta +\eta \frac{f_{\theta }(x^{\prime })}{d\theta }\right)-f(x,\theta )$$

换句话说，

$$k(x,x^{\prime })=\underset{\eta \to 0}{\lim }\frac{f\left(x,\theta +\eta \frac{d{f}_{\theta }(x^{\prime })}{d\theta }\right)-f(x,\theta )}{\eta }$$

我们对$f$进行泰勒近似，根据泰勒公式$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\Delta x$

$$f\left(x,\theta +\eta \frac{d{f}_{\theta }(x^{\prime })}{d\theta }\right)\approx f(x,\theta )+f^{\prime }(x,\theta )\eta \frac{d{f}_{\theta }(x^{\prime })}{d\theta }$$

于是

$$\frac{f\left(x,\theta +\eta \frac{d{f}_{\theta }(x^{\prime })}{d\theta }\right)-f(x,\theta )}{\eta }\approx f^{\prime }(x,\theta )\frac{d{f}_{\theta }(x^{\prime })}{d\theta }=⟨\frac{d{f}_{\theta }(x)}{d\theta },\frac{d{f}_{\theta }(x^{\prime })}{d\theta }⟩$$

我们发现，NTK给予了我们一种“预测”$f(x)$在SGD下变化的能力。那它有一些什么性质呢？

NTK对参数的取值敏感

显然，神经网络可以改变参数，但是保持输出的值不变，那么参数的变化对NTK会有影响吗？答案是有，比如说，上面线性函数的例子将函数改为

$$f_{\theta }(x)={\theta }_{1}x+10{\theta }_2$$

但是设${\theta }_1=3,{\theta }_2=0.1$，你会发现这个函数跟上面是一致的，只是截距项从1变成10*0.1，然而，使用同样的样本$(x,y)=(10,50)$更新这么一个函数，你会发现它的函数变化是不同的：

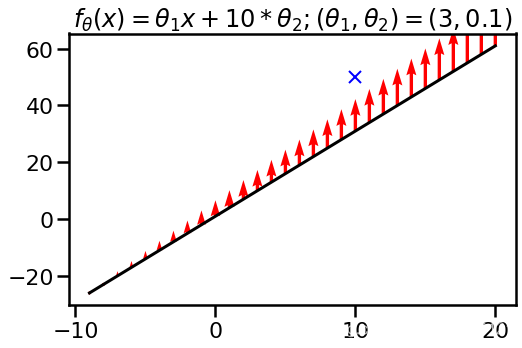
也就是说，NTK对参数是敏感的。

tiny radial basis function network

最后，再来一个小型的神经网络举个例子，考虑函数

$$f_{\theta }(x)={\theta }_1\exp \left(-\frac{(x-{\theta }_2{)}^2}{30}\right)+{\theta }_3\exp \left(-\frac{(x-{\theta }_4{)}^2}{30}\right)+{\theta }_5,$$

初始化为$({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)=(4.0,-10.0,25.0,10.0,50.0)$，同样的，在样本点$(x,y)=(10,50)$更新这么一个函数，我们得到函数的变化为：

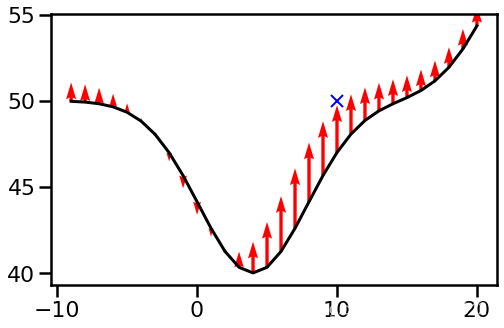
显然，我们发现，在靠近0附近它的变化是很小的，而在10附近它的变化是很大的，之前说过，NTK就是刻画这种变化的，因此，我们可以把NTK画出来：

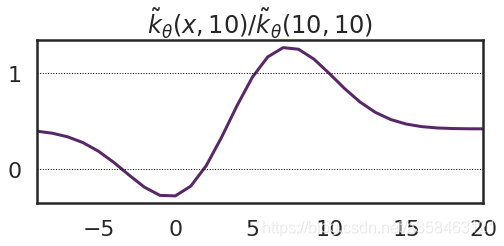
这里除以了在10,10处标准化了一下（只是个除了个常数可以无视），可以发现，确实在0附近的值很小，而在10附近的值很大，符合我们的观察。值得一提的是，虽然样本是$x=10$的点，但是变化最大的地方其实是在$x=7$的地方。

那如果我们不停的更新参数会怎样？以下是更新15次的图

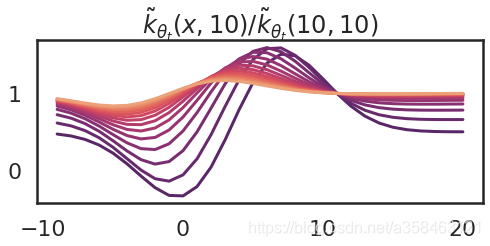
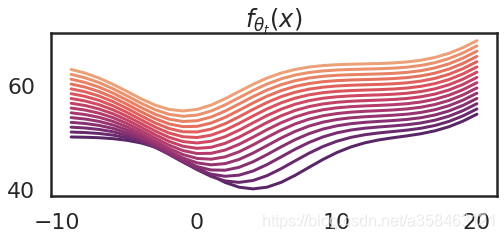
显然，随着参数的变化，kernel大小也在变化，而且越来越平滑，这意味着函数在每个取值下的变化越来越一致。

NTK有什么用？

NTK在无限宽神经网络下有几个非常重要，有用的性质：

1. 在无限宽的网络中，如果参数${\theta }_0$在以某种合适的分布下初始化，那么在该初始值下的NTK$k_{{\theta }_0}$是一个确定的函数，这意味着，不管我的初始值是多少，最终总会收敛到一个确定的核函数上，它与初始化无关！
2. 而且在无限宽网络中，$k_{{\theta }_t}$并不会随着训练的变化而变化，也就是说，在训练中参数的改变并不会改变该核函数。

以上两个事实告诉我们，在无限宽网络中，训练可以理解成一个简单的交kernel gradient descent的算法，而且kernel还是固定的，只取决于网络的结构还有激活函数之类的。这些性质，加上，Neal,(1994)的结论，使得我们可以将这个用梯度下降收敛的极值的概率分布看做是一个随机过程。

最后要注意的就是，这里的NTK，其实是针对梯度下降法提出来的，以往的无限宽网络与高斯过程的联系其实只是在初始化阶段的时候收敛到高斯过程，它并没有说训练过程也是一个高斯过程。它是没有考虑随机梯度下降这一过程的。

而在NTK这里，我们发现，训练的时候与kernel无关，而且初始化决定了它的取值，也就是说，在训练过程中，我们仍然可以认为它还是一个高斯过程而不仅仅是初始化的时候。

参考资料

Some Intuition on the Neural Tangent Kernel

colab notebook