Causal effect可识别的一般条件

最新推荐文章于 2022-07-29 12:38:39 发布

Jie Qiao

最新推荐文章于 2022-07-29 12:38:39 发布

阅读量826

点赞数 1

分类专栏：人工智能

本文链接：https://blog.csdn.net/a358463121/article/details/114196981

版权

人工智能专栏收录该内容

51 篇文章 15 订阅

订阅专栏

Causal effect可识别的一般条件

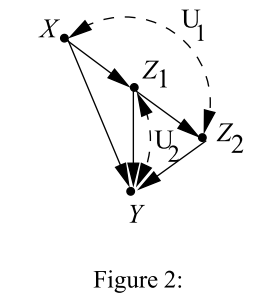
结论：干预后分布 $p (v^{'} ∣ d o (x))$ ，可识别的充要条件是，不存在confounder(隐的共同原因)，连接了X与X的孩子。举个例子，
在这里插入图片描述
上图的 $U_1,U_2$ 是隐变量，该图 $p(y,z_1,z_2|do(x))$ 是可识别的，因为不存在隐变量 $U$ 同时指向X与X的孩子，但是如果我们加一个 $U_3\to X,U_3\to Z_1$ 那就变成不可识别的了。

但这是为什么呢？干预后的分布又是什么意思？我们从干预这个操作开始讲起。

干预后的分布是什么？

先说下因果图的分布是什么？给定一个因果网络，以及变量 $\displaystyle v=\{v_{1} ,...,v_{n} ,x\}$ ，假设没有隐变量，对于分布 $\displaystyle p( v)$ ，可以进行概率分解：

$=\prod _{i} P( v_{i} |pa_{i})$

那如果有隐变量 $\displaystyle u$ ，但是所有隐变量都没有父亲（这种模型也被称为Semi-Markovian model），那么有隐变量的分布就是：

$=\sum _{u}\prod _{i} P\left( v_{i} |pa_{i} ,u^{i}\right) p( u)$

那个干预后的分布，我们可以定义为，强制改变
x的状态，但是其他的状态保持不变，记为 $\displaystyle p_{x}( v) :=p( v'|do( x))$ ，其中 $v^{'}$ 表示不包括x的所有结点。那么对x干预的后果，会使得 $\displaystyle P( v)$ 出现两种情况：

$P_{x}( v) =\begin{cases} \prod _{\left\{i|V_{i}\not{\in } x\right\}} P( v_{i} |pa_{i}) & do( x) 的取值在v中有概率\\ 0 & do( x) 的取值在v中没有概率 \end{cases}$

这是因为干预相当于让一个变量强制100%发生，那么其发生概率只会等于0或1（0的情况就表示这种干预不能发生）. 注意，虽然 $\displaystyle p( do( x) |pa_{x}) =1$ ，但是 $\displaystyle p( y|do( x))$ 不一定等于1的.

类似的，在有隐变量的时候，同样也有干预后的分布为

$P_{x}( v) =\begin{cases} \sum _{u}\prod _{\left\{i|V_{i}\not{\in } x\right\}} P\left( v_{i} |pa_{i} ,u^{i}\right) p( u) & do( x) 的取值在v中有概率\\ 0 & do( x) 的取值在v中没有概率 \end{cases}$

可识别性是什么？–以back door和front door为例

所谓可识别，就是回答以下问题：能不能仅用观测数据就算出 $\displaystyle P_{x}( v)$ ，这个问题在没有隐变量的时候是显然的，因为 $\displaystyle P_{x}( v) =\prod _{\left\{i|V_{i}\not{\in } x\right\}} P( v_{i} |pa_{i})$ ，全部分布都是可观测的，所以一定可以算的。

练习1: 推导大名鼎鼎的back-door准则，设有因果关系 $\displaystyle X\leftarrow Z\rightarrow Y$ 且 $\displaystyle X\rightarrow Y$ ，于是

$\begin{array}{ c c l } & p( do( x) ,y,z) & =p( z)\underbrace{p( do( x) |z)}_{=1} p( y|z,do( x))\\ \Longrightarrow & \sum _{z} p( do( x) ,y,z) & =\sum _{z} p( z) p( y|z,do( x))\\ \Longrightarrow & p( y|do( x))\underbrace{p( do( x))}_{=1} & =\sum _{z} p( z) p( y|z,do( x))\\ \Longrightarrow & p( y|do( x)) & =\sum _{z} p( z) p( y|z,do( x)) \end{array}$

显然这个只适用于没有隐变量的情况。但是有隐变量的时候怎么办？

练习2: 推导大名鼎鼎的fount-door准则

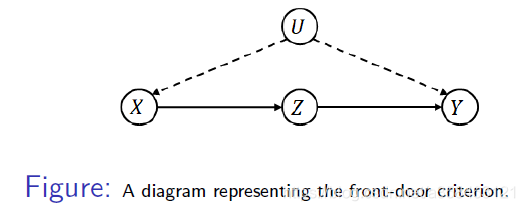
在这里插入图片描述

比如上图的结构，也有一个著名的准则交fount door准则：

$=\sum _{z} p( z|x)\sum _{x} p( y|x,z) p( x)$

这个又是怎么来的呢？我们可以看看，首先

$z|x)\sum _{u} p( x|u) p( y|z,u) p( u)$

全概率这一步很简单但却是及其关键的，因为我们发现 $\displaystyle p( z|x)$ 可以提出来，于是 $\displaystyle \sum _{u} p( x|u) p( y|z,u) p( u) =\frac{p( x,y,z)}{p( z|x)}$ ，这个的作用我们后面说，接来下 $\displaystyle do( x)$ ，于是有：

$x))\sum _{u} p( y|z,u) p( u)$

两边同时对z求和：

$=\sum _{z}\sum _{u} p( z|do( x)) p( y|z,u) p( u) =\sum _{z} p( z|do( x))\sum _{u} p( y|z,u) p( u)$

接下来是关键了，我们发现它大概可以分解成两项，首先第一项是 $\displaystyle p( z|do( x)) =p( z|x)$ ，因为这个分布概率并不会收到do的影响而变化。那么剩下第二项则是 $\displaystyle \sum _{u} p( y|z,u) p( u)$ ，关键的地方来了，我们发现 $\displaystyle \sum _{u} p( x|u) p( y|z,u) p( u) =\frac{p( x,y,z)}{p( z|x)}$ ，用这个表达式是可以消去隐变量的！对比下第二项 $\displaystyle \sum _{z}\sum _{u} p( y|z,u) p( u)$ ，很接近！但还差个 $\displaystyle p( x|u)$ ，那么我们能不能凑这一项出来？然后把隐变量干掉？答案是可以！只需要加一个 $\displaystyle \sum _{x} p( x|u)$ ，于是

$\begin{aligned} \sum _{u} p( y|z,u) p( u) & =\sum _{x}\sum _{z}\sum _{u} p( x|u) p( y|z,u) p( u)\\ & =\sum _{x}\sum _{z}\sum _{u} p( x|u) p( y|z,u) p( u)\\ & =\sum _{x}\sum _{z}\frac{p( x,y,z)}{p( z|x)}\\ & =\sum _{x}\sum _{z}\frac{p( y|z,x) p( z|x) p( x)}{p( z|x)}\\ & =\sum _{x}\sum _{z} p( y|z,x) p( x) \end{aligned}$

最后总体来看：

$\begin{aligned} p( do( x) ,y) & =\sum _{z} p( z|x)\sum _{x}\sum _{z} p( y|z,x) p( x) \end{aligned}$

因为 $\displaystyle p( do( x) ,y) =p( y|do( x)) p( do( x)) =p( y|do( x))$ ，所以我们就得到了front door准则!

$=\sum _{z} p( z|x)\sum _{x} p( y|x,z) p( x)$

其实这里面最关键的一步是用 $\displaystyle \frac{p( x,y,z)}{p( z|x)}$ 进行替换。

可识别的一般条件

从back door和front door的推导，我们可以找出一些规律，首先，我们发现全概率是可以替换掉隐变量的分布的，基于此，我们可以给出一个最简单的情况，设 $\ { X } \displaystyle V'=V\backslash \{X\}$ ，考虑 $\displaystyle p_{x}( v')$ 的可识别性，这里 $\displaystyle v;$ 是除了x的所有贝叶斯网络下的变量.

$=\sum _{u}\prod _{i} P\left( v_{i} |pa_{i} ,u^{i}\right) p( u)$
定理1: 如果没有双向边指向X的时候（X这个变量不存在latent confounder）， $\displaystyle P_{x}( v)$ 可识别

$P_{x}( v') =P( v'|x,pa_{x}) P( pa_{x})$

证明：
因为X没有latent confounder，因此 $\displaystyle p\left( x|pa_{x} ,u^{x}\right) =p( x|pa_{x})$ （x没有隐变量），于是

$\left. \begin{array}{ l } P(v)=p( v'|x) p( x)\\ =P(x|pa_{x} )\sum _{u}\prod _{\{i|V_{i} \neq X\}} P(v_{i} |pa_{i} ,u^{i} )P(u)\\ =P(x|pa_{x} )P (v',do( x) )\\ =P(x|pa_{x} )P(v'|do( x) ) \end{array}\right.$

因此

$P_{x}( v') =\frac{P(v)}{P(x|pa_{x} )} =\frac{P(v'|x,pa_{x}) P( x|pa_{x}) p( pa_{x})}{P(x|pa_{x} )} =P( v'|x,pa_{x}) P( pa_{x})$

证毕。

如果X有隐变量怎么办？另一个有趣的情况则是，如果没有双向边指向所有X直接孩子的话（意味着X和X的子孙(非直接孩子)都是允许存在双向边），我们也能推出一个可识别的公式。

定理2 如果所有X的直接孩子都没有双向边，则 $\displaystyle P_{x}( v')$ 可识别，

$P_{x} (v')=\left(\prod _{\{i|V_{i} \in Ch_{x} \}} P(v_{i} |pa_{i} )\right)\sum _{x}\frac{P(v)}{\prod _{\{i|V_{i} \in Ch_{x} \}} P(v_{i} |pa_{i} )}$

证明：
令 $\ ( c h x ∪ { X } ) , A = ∏ { i ∣ V i ∈ S } P ( v i ∣ p a i , u i ) \displaystyle S=V\backslash ( ch_{x} \cup \{X\}) ,A=\prod _{\{i|V_{i} \in S\}} P(v_{i} |pa_{i} ,u^{i} )$ . 因为所有X的孩子都没有隐变量，所以全概率可以分解为两部分：

$\ ( c h x ∪ { X } ) P ( v i ∣ p a i , u i ) ⏟ A ⋅ p ( u ) p( v) =\prod _{\{i|V_{i} \in ch_{x} \}} P(v_{i} |pa_{i} ,u^{i} )\sum _{u} p\left( x|pa_{x} ,u^{x}\right) \cdotp \underbrace{\prod _{V\backslash ( ch_{x} \cup \{X\})} P(v_{i} |pa_{i} ,u^{i} )}_{A} \cdotp p( u)$

一部分是X的孩子(没有隐变量，所以可以提出来)，另一部分是其余的变量。又因为 $\displaystyle p( do( x) |pa_{x}) =1$ ，所以

$=\prod _{\{i|V_{i} \in ch_{x} \}} P(v_{i} |pa_{i} ,u^{i} )\sum _{u} A\cdotp p( u)$

好了，关键一步来了，跟之前类似，我们发现干预分布跟全概率分布长得很像，大家都有一个 $\displaystyle Ap( u)$ ，就是缺了 $\displaystyle p\left( x|pa_{x} ,u^{x}\right)$ ，所以自然的，我们可以在干预分布里强行加进去，利用 $\displaystyle \sum _{x} p\left( x|pa_{x} ,u^{x}\right) =1$ ，这样我们就能借助全概率来消掉干预分布的隐变量。而且，因为A是排除了所有X与X的子代的变量，因此A不包含x，于是，

$\begin{aligned} p( do( x) ,v') & =\prod _{\{i|V_{i} \in ch_{x} \}} P(v_{i} |pa_{i} ,u^{i} )\sum _{x}\sum _{u} p\left( x|pa_{x} ,u^{x}\right) A\cdotp p( u)\\ & =\prod _{\{i|V_{i} \in ch_{x} \}} P(v_{i} |pa_{i} ,u^{i} )\sum _{x}\frac{p( v)}{\prod _{\{i|V_{i} \in ch_{x} \}} P(v_{i} |pa_{i} ,u^{i} )} \end{aligned}$

证毕。

总结下，最重要的一步仍然是想办法用全概率将隐变量干掉，我们发现，当X的孩子没有隐变量的时候是可以干掉的，如果X的孩子有隐变量，那么A中就会包含X，这时候就不一定了。所以接来下的问题是什么时候可行，什么时候不可行？

如下图

在这里插入图片描述

显然，这个图里面X的孩子是由双向边 $\displaystyle U_{2}$ 的，但他却是可以识别的。为什么？我们可以来推导下：

$P(v)=\underbrace{\sum _{u_{1}} P(x|u_{1} )P(z_{2} |z_{1} ,u_{1} )P(u_{1} )}_{Q_{1}} \cdot \underbrace{\sum _{u_{2}} P(z_{1} |x,u_{2} )P(y|x,z_{1} ,z_{2} ,u_{2} )P(u_{2} )}_{Q_{2}}$

我们发现 $\displaystyle p( v)$ 分解成两部分，分别由 $\displaystyle u_{1} ,u_{2}$ 两个求和组成，并且，这两部分对应的恰好是隐变量confounder导致的，这两部分，分别被confounder形成的分布，在后文会被称为c-factor. 于是，考虑干预后分布，因为 $\displaystyle p( do( x) |u_{1}) =1$ , 我们有

$P_{x} (v')=\sum _{u_{1}} P(z_{2} |z_{1} ,u_{1} )P(u_{1} )\cdot \underbrace{\sum _{u_{2}} P(z_{1} |x,u_{2} )P(y|x,z_{1} ,z_{2} ,u_{2} )P(u_{2} )}_{Q_{2}}$

对比全概率公式，我们发现只缺了一项 $\displaystyle P(x|u_{1} )$ 所以我们补回去，就有

$\begin{aligned} P_{x} (v') & =\underbrace{\sum _{u_{2}} P(z_{1} |x,u_{2} )P(y|x,z_{1} ,z_{2} ,u_{2} )P(u_{2} )}_{Q_{2}} \cdot \sum _{x}\underbrace{\sum _{u_{1}} P(x|u_{1} )P(z_{2} |z_{1} ,u_{1} )P(u_{1} )}_{Q_{1}}\\ & =Q_{2}\sum _{x} Q_{1} \end{aligned}$

这意味着，如果 $\displaystyle Q_{1}$ 和 $\displaystyle Q_{2}$ 这两部分都是可识别的（可从观测数据恢复），他们的整体就是可识别的！实际上，因为 $\displaystyle p( v) =Q_{1} Q_{2}$ ，所以只要其中一个，比如 $\displaystyle Q_{1}$ 可识别，另一个就可以识别 $\displaystyle Q_{2} =\frac{p( v)}{Q_{1}}$ . 那 $\displaystyle Q_{1}$ 要怎么识别呢？我们要想办法把 $\displaystyle u_{2}$ 的部分干掉，但是又不能像之前一样用全概率（否则 $\displaystyle Q_{2}$ 就没法恢复了），怎么办？虽然不能用所有变量的全概率，但是我们可以用部分结点的全概率啊！仔细观察全概率的分解， $\displaystyle y$ 只出现在 $\displaystyle Q_{2}$ 中，所以可以通过求和(积分)把y干掉，得到只有3个变量的全概率！：

$\sum _{y} P(v)=P( x,z_{1} ,z_{2}) =\underbrace{\sum _{u_{1}} P(x|u_{1} )P(z_{2} |z_{1} ,u_{1} )P(u_{1} )}_{Q_{1}} \cdot \sum _{u_{2}} P(z_{1} |x,u_{2} )P(u_{2} )$

而且把y干掉之后，我们又发现， $\displaystyle z_{2}$ 只出现在 $\displaystyle Q_{1}$ 中，所以也可以把他干掉：

$\sum _{y}\sum _{z_{2}} P(v)=P( x,z_{1}) =P(x) \cdot \sum _{u_{2}} P(z_{1} |x,u_{2} )P(u_{2} )$

这样我们就得到两个部分变量的全概率分解。显然，用这两个全概率分解相除， $\displaystyle u_{2}$ 被消干掉了！

$\frac{P( x,z_{1} ,z_{2})}{P( x,z_{1})} =\frac{Q_{1}}{P(x)}\\ \Longrightarrow Q_{1} =\frac{P( x,z_{1} ,z_{2})}{P( x,z_{1})} P(x) =\frac{P( z_{2} |z_{1} ,x) P( z_{1} |x) p( x)}{P( z_{1} |x)} =P( z_{2} |z_{1} ,x) p( x)\\ \Longrightarrow Q_{2} =\frac{P( v)}{Q_{1}} =\frac{P( y|z_{1} ,z_{2} ,x) P( z_{2} |z_{1} ,x) P( z_{1} |x) P( x)}{P( z_{2} |z_{1} ,x) p( x)} =P( y|z_{1} ,z_{2} ,x) P( z_{1} |x)$

于是，我们终于得到干预后的分布：

$\begin{aligned} P_{x} (v') & =Q_{2}\sum _{x} Q_{1}\\ & =P( y|z_{1} ,z_{2} ,x) P( z_{1} |x)\sum _{x'} P( z_{2} |z_{1} ,x') p( x') \end{aligned}$

C-components

从上面可以看出，最关键的地方就是分解成 $\displaystyle Q_{1} ,Q_{2}$ 的两部分，而这两部分从图上就是不重叠的两个confounder组成的，所以v可以分解为多个component的乘积

$=\prod ^{k}_{j=1} Q_{j}$

其中每个Q都对应一组隐变量的confounder的集合 $\displaystyle n_{j}$ ，他们有着重合的孩子 $\displaystyle S_{j}$ ，于是:

$Q_{j} =\sum _{n_{j}}\prod _{\{i|V_{i} \in S\}} p\left( v_{I} |pa_{i} ,u^{i}\right) P( n_{j})$

我们称 $\displaystyle S_{J}$ 为c-component (confounded component)， $\displaystyle Q_{j}$ 为c-factor. 最重要的是，我们可以证明，所有的 $\displaystyle Q_{j}$ 都是可识别的！，换句话说，如果我们能将干预后的分布变成 $\displaystyle Q$ 的组合，那么干预后的分布就是可识别的了！并且每个 $\displaystyle Q$ 长这样：

$Q_{j} =\prod _{\{i|V_{i} \in S\}} p\left( v_{i} |v^{( i-1)}\right)$

这里 $\displaystyle v^{( i-1)}$ 表示的是在causal order排列下，所有排在 $\displaystyle v_{i}$ 后的变量。显然，如果整个图只有一个 $\displaystyle Q$ ，那么 $\displaystyle Q=p( v_{1} |v_{2} ,...v_{n}) p( v_{2} |v_{3} ,...,v_{n}) ...p( v_{n})$ 就是全概率分解.

那在什么情况下干预的分布可以写成Q的组合呢？论文[1]指出，当且仅当在没有任何双向边将X与X的孩子连起来就足够了。于是这个干预后的分布可以写成：

$\begin{aligned} P_{x} (v') & =Q^{X}_{x}\prod _{i} Q_{i} =Q^{X}_{x}\frac{p( v)}{Q^{X}}\overset{( i)}{=}\left(\sum _{x} Q^{X}\right)\frac{p( v)}{Q^{X}}\\ P(v) & =Q^{X}\prod _{i} Q_{i} \end{aligned}$

其中 $\displaystyle Q^{X}$ 是X对应的c-factor，而 $\displaystyle Q^{X}_{x}$ 是把 $\displaystyle Q^{X}$ 中的 $\displaystyle p\left( x|pa_{x} ,u^{x}\right)$ 删掉：

$Q^{X}_{x} =\sum _{n^{X}}\prod _{\{i|V_{i} \neq X,V_{i} \in S^{X} \}} p\left( v_{i} |pa_{i} ,u^{i}\right) p\left( n^{X}\right)\\ Q^{X} =\sum _{n^{X}}\prod _{\{i|V_{i} \in S^{X} \}} p\left( v_{i} |pa_{i} ,u^{i}\right) p\left( n^{X}\right)$

注意等式 $\displaystyle Q^{X}_{x}\frac{p( v)}{Q^{X}}\overset{( i)}{=}\left(\sum _{x} Q^{X}\right)\frac{p( v)}{Q^{X}}$ ，右边是只有在没有任何双向边将X与X的孩子连起来的时候才成立，但是左边是恒成立的。所以证明的关键就是等式 $\displaystyle Q^{X}_{x} =\left(\sum _{x} Q^{X}\right)$ 能否成立。事实上，他们的差别就是一个将 $\displaystyle p\left( x|pa_{x} ,u^{x}\right)$ 直接删掉，令一个是对x进行求和/积分，那在什么情况下这两个操作的结果是一致的呢？答案是在 $\displaystyle Q^{X}$ 中，所有的 $\displaystyle p\left( v_{i} |pa_{i} ,u^{i}\right)$ 里面的 $\displaystyle pa_{i}$ 都不包括 $\displaystyle x$ 的时候，对x求和，跟直接删掉 $\displaystyle p\left( x|pa_{x} ,u^{x}\right)$ 是等价的。换句话说，如果存在一个confounder连接了X跟X的孩子，使得他们出现在同一个c-conponent $\displaystyle Q^{X}$ 中，导致其中的某个结点的父亲 $\displaystyle pa_{i}$ ，出现了 $\displaystyle x$ ，这时候求和是没法将 $\displaystyle p\left( x|pa_{x} ,u^{x}\right)$ 删掉的，从而导致 $\displaystyle Q^{X}$ 这一项不可识别。这就是证明的直观过程。具体过程，有兴趣自己看[1].

参考资料

Tian J, Pearl J. A general identification condition for causal effects[C]//Aaai/iaai. 2002: 567-573.

An Overview of The Back-Door and Front-Door Criteria

Jie Qiao

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
1
评论
Causal effect可识别的一般条件

Causal effect可识别的一般条件结论：干预后分布p(v′∣do(x))p(v'|do(x))p(v′∣do(x))，可识别的充要条件是，不存在confounder(隐的共同原因)，连接了X与X的孩子。举个例子，上图的U1,U2U_1,U_2U1,U2是隐变量，该图p(y,z1,z2∣do(x))p(y,z_1,z_2|do(x))p(y,z1,z2∣do(x))是可识别的，因为不存在隐变量UUU同时指向X与X的孩子，但是如果我们加一个U3→X,U3→Z1U_3\to X,U_3\to
复制链接

扫一扫