玩转数据结构之Java实现二叉堆

原创 已于 2023-02-10 22:05:33 修改 · 392 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#java #数据结构 #算法

于 2023-02-08 20:06:01 首次发布
文章介绍了如何使用Java自定义动态数组实现最大二叉堆，包括插入、删除、查找等操作，并基于最大堆构建了优先级队列，讨论了相关的时间复杂度。

前言

二叉堆是一颗完全二叉树，并满足堆中某个节点的值总是小于或等于父节点的值；
二叉堆
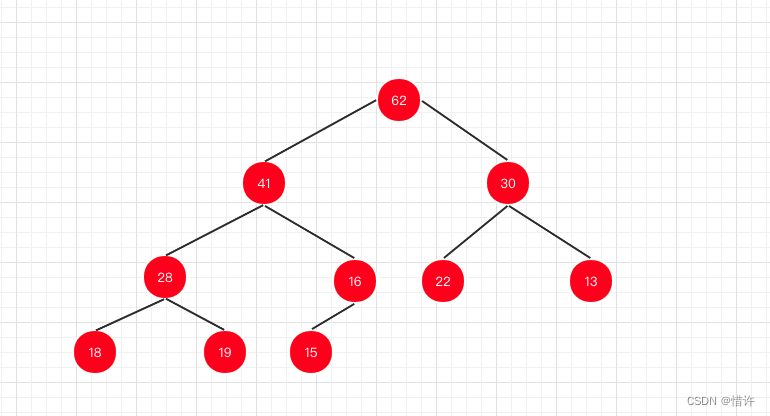
最大堆：根节点元素最大值；
最小堆：根节点元素最小值；

代码实现

基于数组实现最大二叉堆

  • 自定义动态数组
package com.sjgd.heap;

/**
 * 自定义动态数组
 */
public class Array<E> {
    /**
     * 维护的数组
     */
    private E[] data;
    /**
     * 数组中元素的个数
     */
    private int size;

    public Array(int capacity) {
        data = (E[]) new Object[capacity];
        size = 0;
    }

    public Array(E[] arr) {
        data = (E[]) new Object[arr.length];
        System.arraycopy(arr, 0, data, 0, arr.length);
        size = arr.length;
    }

    public Array() {
        this(10);
    }

    /**
     * 获取数组的融了
     *
     * @return
     */
    public int getCapacity() {
        return data.length;
    }

    /**
     * 获取数组中元素的个数
     *
     * @return
     */
    public int getSize() {
        return size;
    }

    /**
     * 判断数组是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return size == 0;
    }


    /**
     * 在数组的index索引插入一个新的元素
     */
    public void add(int index, E e) {
        if (index < 0 || index > size) {
            throw new IllegalArgumentException("Add Failed, Require index >=0 and index <= size");
        }
        if (size == data.length) {
            //说明当前数组已满，需要进行扩容
            resize(2 * data.length);
        }
        //索引位置后面的元素都需要往后移1个位置
        for (int i = size - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        data[index] = e;
        size++;
    }

    /**
     * 向一个位置添加元素E
     */
    public void addFirst(E e) {
        add(0, e);
    }

    /**
     * 向最后一个位置添加元素E
     *
     * @param e
     */
    public void addLast(E e) {
        add(size, e);
    }

    /**
     * 根据index获取索引对应的元素E
     *
     * @param index
     * @return
     */
    public E get(int index) {
        if (index < 0 || index >= size) {
            throw new IllegalArgumentException("Get Failed, Index is illegal!");
        }
        return data[index];
    }

    /**
     * 交换数组中两个元素的位置
     */
    public void swap(int i, int j) {
        if (i < 0 || i >= size || j < 0 || j >= size) {
            throw new IllegalArgumentException("The Index is not Illegal");
        }
        E e = data[i];
        data[i] = data[j];
        data[j] = e;
    }

    /**
     * 修改index索引位置对应的元素
     *
     * @param index
     * @param e
     */
    public void set(int index, E e) {
        if (index < 0 || index >= size) {
            throw new IllegalArgumentException("Add Failed, Require index >=0 and index <= size");
        }
        data[index] = e;
    }


    /**
     * 判断当前数组是否包含元素E
     *
     * @param e
     * @return
     */
    public boolean contains(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e)) {
                return true;
            }
        }
        return false;
    }

    /**
     * 查询元素E对应的下标位置
     *
     * @param e
     * @return
     */
    public int find(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e)) {
                return i;
            }
        }
        return -1;
    }


    public E remove(int index) {
        if (index < 0 || index >= size) {
            throw new IllegalArgumentException("remove Failed, Require index >=0 and index < size");
        }
        E ret = data[index];
        //从删除索引位置之后元素均向前移一位
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        size--;
        //进行空间释放
        data[size] = null;
        //当数组元素到容量1/4时，进行缩容操作
        if (size == data.length / 4 && data.length / 2 != 0) {
            resize(data.length / 2);
        }
        return ret;
    }

    /**
     * 移除第一个元素
     *
     * @return
     */
    public E removeFirst() {
        return remove(0);
    }

    /**
     * 移除最后一个元素
     *
     * @return
     */
    public E removeLast() {
        return remove(size - 1);
    }

    /**
     * 移除对应元素e
     *
     * @param e
     */
    public void removeElement(E e) {
        int index = find(e);
        if (index != -1) {
            remove(index);
        }
    }


    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("Array size=%d, capacity=%d\n", size, data.length));
        stringBuilder.append("[");
        for (int i = 0; i < size; i++) {
            stringBuilder.append(data[i]);
            if (i != size - 1) {
                stringBuilder.append(",");
            }
        }
        stringBuilder.append("]");
        return stringBuilder.toString();
    }

    /**
     * 对数组进行动态扩容或缩容
     *
     * @param newCapacity
     */
    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newData[i] = data[i];
        }
        data = newData;
    }
}
  • 实现最大二叉堆
package com.sjgd.heap;

/**
 * 基于数组实现最大堆
 * on 2023/2/8
 */
public class MaxHeap<E extends Comparable<E>> {
    private Array<E> array;

    public MaxHeap(int capacity) {
        array = new Array<>(capacity);
    }

    public MaxHeap() {
        array = new Array<>();
    }

    public MaxHeap(E[] arr) {
        array = new Array<>(arr);
        for (int i = parent(array.getSize() - 1); i >= 0; i--) {
            siftDown(i);
        }
    }

    /**
     * 返回堆中元素的个数
     *
     * @return
     */
    public int size() {
        return array.getSize();
    }

    /**
     * 返回一个布尔值，判断当前堆是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return array.isEmpty();
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引所表示的元素的父节点所有的索引
     *
     * @return
     */
    private int parent(int index) {
        if (index == 0) {
            throw new IllegalArgumentException("index 0 doesn't have parent.");
        }
        return (index - 1) / 2;
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
     *
     * @return
     */
    private int leftChild(int index) {
        return index * 2 + 1;
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
     *
     * @return
     */
    private int rightChild(int index) {
        return index * 2 + 2;
    }

    /**
     * 往最大堆中添加元素e
     *
     * @param e
     */
    public void add(E e) {
        array.addLast(e);
        siftUp(array.getSize() - 1);
    }


    public E removeMax() {
        E result = getMax();
        //先交换最大值和最后一个元素的位置
        array.swap(0, array.getSize() - 1);
        //删除最后一个元素
        array.removeLast();
        siftDown(0);
        return result;
    }

    public E getMax() {
        if (array.getSize() == 0) {
            throw new IllegalArgumentException("The MaxHeap is Empty!");
        }
        return array.get(0);
    }

    /**
     * 取出堆中最大元素，并替换成元素e
     *
     * @return
     */
    public E replace(E e) {
        E result = getMax();
        array.set(0, e);
        siftDown(0);
        return result;
    }


    /**
     * 不断与左右子节点中较大的比较并交换，直到满足最大堆要求；
     *
     * @param index
     */
    private void siftDown(int index) {
        while (leftChild(index) < array.getSize()) {
            int leftChildIndex = leftChild(index);
            int rightChildIndex = leftChildIndex + 1;
            if (rightChildIndex < array.getSize() && array.get(leftChildIndex).compareTo(array.get(rightChildIndex)) < 0) {
                leftChildIndex = rightChildIndex;
            }
            if (array.get(index).compareTo(array.get(leftChildIndex)) > 0) {
                break;
            }
            array.swap(index, leftChildIndex);
            index = leftChildIndex;

        }
    }

    /**
     * 不断与父节点元素进行对比，如果大于父节点元素不断交换两者位置，直到满足最大堆要求;
     *
     * @param index
     */
    private void siftUp(int index) {
        while (index > 0 && array.get(index).compareTo(array.get(parent(index))) > 0) {
            array.swap(index, parent(index));
            index = parent(index);
        }
    }
}
  • 基于MaxHeap实现优先级队列；
package com.sjgd.heap;

/**
 * @author 基于MaxHeap实现优先级队列
 * on 2023/2/8
 */
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
    private MaxHeap<E> maxHeap;

    public PriorityQueue() {
        maxHeap = new MaxHeap<>();
    }

    @Override
    public int getSize() {
        return maxHeap.size();
    }

    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }

    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }

    @Override
    public E dequeue() {
        return maxHeap.removeMax();
    }

    @Override
    public E getFront() {
        return maxHeap.getMax();
    }
}

时间复杂度

入队出队：O（logn）

结语

如果以上文章对您有一点点帮助，希望您不要吝啬的点个赞加个关注，您每一次小小的举动都是我坚持写作的不懈动力！ღ( ´･ᴗ･` )

【数据结构】建立二叉树、二叉树的推导技巧
四季轮换叶，一路招摇胜
05-07 5284
逆向思维指的是反向思考问题的能力。而我们的二叉树的建立推导过程，就是运用了逆向思维。在得到的二叉树前序、中序、后序遍历的结果后，在根据2种不同的遍历结果，反向推导出二叉树集合。...
数据结构之优先队列--二叉堆(Java实现)
热门推荐
LCore的专栏
06-16 1万+
前言               数据结构队列的学习中，我们知道队列是先进先出的。任务被提交到队列中，按照先进先出的原则      对各个任务进行处理。不过在现实的情况下，任务通常有着优先级的概念，例如短任务、管理员的操作      应该优先执行。这是使用队列就无法描述了，这种特殊的应用我们使用一种称之为优先队列(堆)的方式      来解决。   优先队列             和
二叉堆（JAVA实现）
nvnnv的博客
04-04 838
定义二叉堆（简称堆，当然还有别的堆），是一种具有特定规则的树形结构，二叉堆规定：父节点的值必定大于（小于）其孩子节点，因此可以称其为最大堆（最小堆），堆是维护极值的非常快速的一种数据结构。实现思路堆一般都是数组实现的（不明白用数组怎么写树的，请自己脑补，很容易想的）。 拿最小堆来说，堆的根节点一定是最小的，堆只可以从根节点取值，所以堆的调整是最重要的工作。 比如对数列： 10 1 11 9 6
java-二叉堆（堆）binaryHeap
08-05
4.binaryHeap 二叉堆 支持排序，父子之间只有一种大小关系。孩子大于父，或者小于父。 二叉堆不支持合并。 实现了各种增删查改算法。
二叉堆最小堆的Java实现
03-01
个人实现的最小权重的二叉堆实现，效率很高，适合任意场合下的临时列表排序。 可在外部写脚本对该文件进行测试 需要继承Tuple类实现排序对象类型，并实现Tuple的抽象方法weight()来反映排序对象权重
java 二叉堆
qq_35578760的博客
11-16 255
二叉堆的本质还是数组，完全二叉堆是建立完全二叉树的基础上的，二叉堆又分为大顶堆和小定堆，大顶堆就是父节点的值大于左右孩子的两个节点的值，小顶堆就是父节点的值小于左右孩子节点的值。堆的自我调整包括删除节点和添加节点，添加节点是在二叉堆的最后一个位置上添加，删除节点是删除根节点的值。然后左右孩子的重新调整成一个二叉堆。二叉堆的构建就是让一个无序的完全二叉树调成成二叉堆，本质就是让所有非叶子节点上升或者...
什么是二叉堆/java实现
罗伯特是疯子丶
09-11 573
堆的定义 二叉堆是一种特殊的堆，可以看做是完全二叉树，它分为两个类型： 1.最大堆 2.最小堆 什么是最大堆呢？就是父结点的键值总是大于或等于任何一个子节点的键值； 什么是最小堆呢？父结点的键值总是小于或等于任何一个子节点的键值。 其中二叉堆的根节点叫...
玩转数据结构
06-08 317
数组时间复杂度 将1次resize均摊给2n+1；所以每次addLast操作，进行2次基本操作；均摊时间复杂度O(1) 复杂度震荡 addLast和removeLast操作同时考虑： 在n/2时，这个临界点，扩容和缩容； 解决方案：Lazy 当数组中的数据为实际的1/4时，再进行缩容操作 data.length / 2 != 0 //当数组元素；当data.length等于1时，数组不能分配0个大小； 栈和队列 栈是一种线性结构； 只能从一端添加元素，也只..
Java -数据结构，【优先级队列 / 堆】
ryy1999的博客
03-04 928
1、如果求前K个最大的元素，要建一个小根堆。2、如果求 前K个最小的元素，要建一个大根堆。3、如果是求第k大的元素，建一个小堆，小根堆 堆顶的元素就是第k大的元素。4、如果是求第k小的元素，建一个大堆，大根堆 堆顶的元素就是第k小的元素。
数据结构--Java语言描述
The_last_knight的博客
09-29 1009
本篇文章是为了记录自己在学习数据结构时的笔记，会对常见的数据结构做基本的介绍以及使用Java语言进行实现。包括 动态数组 栈 队列 链表 二分搜索树 优先队列和堆 线段树 Trie树 并查集 AVL树 红黑树 哈希表 动态数组 API介绍 数组是一种根据下标操作的数据结构，它的查询速度很快，但是它有缺点，那就是数组的容量一旦在创建时确定，就不能进行更改，所以为了克服这一缺点，我们实现一个自己的...
Java实现剑指offer算法与排序数据结构详解
- 堆排序：利用堆这种数据结构进行排序的方法，堆是一种近似完全二叉树的结构，并同时满足堆积的性质。 #### 数据结构 数据结构是计算机存储、组织数据的方式。文件中提到了两种数据结构： - 循环队列：一种队列的...
使用Java实现二叉堆
最新发布
Weirdo的博客
05-30 466
本文详细介绍了二叉堆的基本原理和主要操作，并使用Java编程语言实现了一个简单的二叉堆。二叉堆是一种非常有用的数据结构，常用于实现优先队列等算法。通过本文的学习，读者应该能够理解二叉堆的工作原理，并能够在自己的项目中使用它。
java 数据结构之二叉堆
cyt
01-11 355
树的基本概念 节点的度： 这个节点子树的个数 树的度： 所有节点中度的最大值 叶子节点： 度为0的节点 非叶子节点： 度不是0的节点 节点的深度： 从根节点到当前节点唯一路径上的节点总数 节点的高度： 从当前节点到最远叶子节点的路径上的节点总数 树的深度： 所有节点深度的最大值 树的高度： 所有节点高度的最大值 树的深度等于树的高度 有序树 树中任意节点的子节点之间有顺序的关系 无序树 树中任意节点的子节点之间没有顺序关系 二叉树 每个节点度的最大值为 2 一个节点最多拥有2个子树 左子
堆(二叉堆)-优先队列-数据结构和算法(Java)
gaogzhen的博客
12-04 703
堆(二叉堆)-优先队列-数据结构和算法(Java)
java实现二叉堆,数据结构基础篇-二叉堆
weixin_34268617的博客
03-15 307
二叉堆分为两种，最大堆和最小堆，我们只讨论最小堆的性质，最大堆具有相同的原理。最小堆是一种符合下面两个特性的树形结构：最小堆是一颗完全二叉树，即最小堆的每个节点要么没有子节点，要么只有一个左子节点，要么有两个子节点。最小堆的每个节点都小于等于它的子节点。堆的基本操作从性质2可以得出一个结论，最小堆的堆顶元素，一定是堆中最小的元素。最小堆可以支持以下几种基本操作：pop，移除堆顶元素，然后堆要做一些...
二叉堆的简单实现（Java）
Mrrr_Li的博客
12-23 290
堆的基本接口设计 ◼ int size(); // 元素的数量 ◼ boolean isEmpty(); // 是否为空 ◼ void clear(); // 清空 ◼ void add(E element); // 添加元素 ◼ E get(); // 获得堆顶元素 ◼ E remove(); // 删除堆顶元素 ◼ E replace(E element); // 删除堆顶元素的同时插入一个新元素 ◼ 二叉堆的逻辑结构就是一棵完全二叉树，所以也叫完全二叉堆 ◼ 鉴于完全二叉树的一些特性，二叉堆的底层（物
算法(第四版)学习笔记之java实现基于堆的优先队列
seabear008的专栏
07-25 1597
一台电脑之所以能同时运行多个应用程序的时候，是通过为每个应用程序的事件分配一个优先级，并总是处理下一个优先级最高的事件来实现的。在这种情况下，一个合适的数据结构应该支持两种操作：删除最大元素和插入元素。我们称这种数据类型叫做优先队列。 优先队列是一种抽象数据类型，它表示了一组值和对这些值的操作，其中最重要的操作就是删除最大元素和插入元素。 数据结构二叉堆能够很好地实现优先队列的基本操作。在二叉
Java实现二叉堆创建
软货成熊之路
07-05 702
问题描述二叉堆数据结构可以是一个数组对象，他可以视为一个几乎完全的二叉树，最大堆满足对于每一个非根节点，节点的值不大于其父节点的值。程序实现public class MaxHeap { public static int left(int i){ return 2*i; } public static int right(int i){ ret
java 二叉堆_二叉堆的介绍和Java实现
weixin_39564187的博客
02-16 386
一、堆和二叉堆堆，英文名称Heap，所谓二叉堆(也有直接称二叉堆为堆的)，本质上是一个完全二叉树，前面也提到过，如果树接近于完全二叉树或者满二叉树，采用顺序存储代价会小一点，因此常见的二叉堆均是顺序实现的。按照排列的顺序可以分为最大堆和最小堆，最大堆的特征是父节点一定大于(依据情况判断是大于等于还是严格大于，数据结构归根到底还是用来使用的)子节点的数据。同样，有最大堆就会有最小堆，最小堆的 父节点...
JAVA后台构建树结构数据返回前端的实现
"这篇文章主要讲解了如何在Java后端将数据转换为树结构，并返回给前端，以便前端可以直接使用。作者通过示例代码详细阐述了实现这一过程的方法，包括使用递归的方式构建树形结构。" 在开发Web应用时，处理树形结构...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值