《编程之美》找符合条件的数

转载自：http://blog.csdn.net/jcwKyl/article/details/3859155

题目：任意给定一个正整数N，求一个最小的正整数M(M>1)，使得N*M的十进制表示形式里只含有1和0.

解决这个问题首先考虑对于任意的N，是否这样的M一定存在。可以证明，M是一定存在的，而且不唯一。
简单证明：因为

 

这是一个无穷数列，但是数列中的每一项取值范围都在[0, N-1]之间。所以这个无穷数列中间必定存在循环节。即假设有s,t均是正整数，且s<t，有 。于是循环节长度为t-s。于是10^s = 10^t。因此有：
，所以

例如，取N＝3，因为10的任何非负次方模3都为1，所以循环节周期为1.有：

给定N，求M的方法：
方法一 ：给定N，令M从2开始，枚举M的值直到遇到一个M使得N*M的十进制表示中只有1和0.
方法二 ： 求出10的次方序列模N的余数序列并找出循环节。然后搜索这个余数序列，搜索的目的就是要在这个余数序列中找到一些数出来让它们的和是N的倍数。例如N=13，这个序列就是1,10,9,12,3,4然后不断循环。很明显有1+12=13，而1是10的0次方，12是10的3次方，所以这个数就是1000+1=1001，M就是1001/13=77。
方法三 ：因为N*M的取值就是1,10,11,100,101,110,111,......所以直接在这个空间搜索，这是对方法一的改进。搜索这个序列直到找到一个能被N整除的数，它就是N*M，然后可计算出M。例如N=3时，搜索树如下：

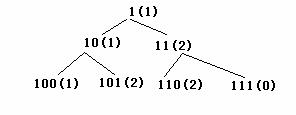
使用广度遍历二叉树！！！
上图中括号内表示模3的余数。括号外表示被搜索的数。左子树表示0，右子树表示1.上图中搜索到第二层（根是第0层）时遇到111，它模3余数为0.所以N*M=111, M=111/3=37。
方法四：对方法三的改进。将方法三的搜索空间按模N余数分类，使得搜索时间和空间都由原来的指数级降到了O(N)。改进的原理：假设当前正在搜索由0，1组成的K位十进制数，这样的K位十进制数共有2^k个。假设其中有两个数X、Y，它们模N同余，那么在搜索由0、1组成的K+1位十进制数时，X和Y会被扩展出四个数：10X, 10X+1, 10Y, 10Y+1。因为X和Y同余（同余完全可以看作相等），所以10X与10Y同余，10X+1与10Y+1同余。也就是说由Y扩展出来的子树和由X扩展产生出来的子树产生完全相同的余数，如果X比Y小，那么Y肯定不是满足要求的最小的数，所以Y这棵子树可以被剪掉。这样，2^K个数按照模N余数分类，每类中只保留最小的那个数以供扩展。原来在这一层需要搜索2^K个数，现在只需要搜索O(N)个数。例如，当N=9时，第0层是1(1)，

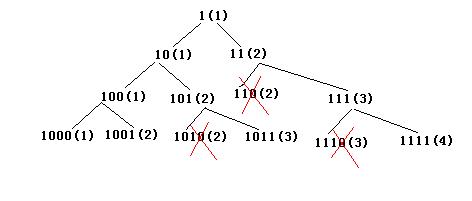
如上图所示，第2层的110，第三层的1010、1110都因为同一层有和它同余且更小的数而被剪掉。如果按照方法三搜索，第三层本来应该有8个结点，但现在只有4个结点。

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

struct QNode
{
	long long v;//表示值的大小，小心溢出
	int r;//表示对N的余数
	QNode(long long vv,int rr):v(vv),r(rr){};
};

int main(int argc,char* argv[])
{
	int n;
	cin>>n;
	vector<bool> FindMinMod(n,false);//用来表示一个同余数组，如 FindMinMod【i】表示是否已经找到了余数为i的最小的那个
	queue<QNode> q;
	q.push(QNode(1,1));//从一位数1开始
	while(!q.empty())//利用的是广度优先搜索，当一个循环序列过去没有找到，要求的x退出
	{
		QNode t=q.front();
		if(t.r==0)//找到最小的值输出
		{
			cout<<t.v/n<<endl;
			break;
		}
		q.pop();
		if(!FindMinMod[(t.r*10)%n])//判断10X的余数
		{
			FindMinMod[t.r*10%n]=true;
			q.push(QNode(t.v*10,t.r*10%n));
		}
		if(!FindMinMod[(t.r * 10 + 1) % n])//判读10x+1的余数
		{  
			FindMinMod[(t.r * 10 + 1) % n] = true;  
			q.push(QNode(t.v * 10 + 1, (t.r * 10 + 1) % n));
		}  
	}
	system("pause");
	return 0;
}