原文地址: http://www.mvstat.net/tduong/research/seminars/seminar-2001-05/
This talk is divided into three parts: first is on histograms, on how to construct them andtheir properties. Next are kernel density estimators – how they are a generalisation andimprovement over histograms. Finally is on how to choose the most appropriate, ‘nice’kernels so that we extract all the important features of the data.
A histogram is the simplest non-parametric density estimator and the one that is mostlyfrequently encountered. To construct a histogram, we divide the interval covered by the datavalues and then into equal sub-intervals, known as ‘bins’. Every time, a data value falls intoa particular sub-interval, then a block, of size equal 1 by the binwidth, is placed on top of it.When we construct a histogram, we need to consider these two main points: the size of thebins (the binwidth) and the end points of the bins.
The data are (the log of) wing spans of aircraft built in from 1956 – 1984. (The completedataset can be found in Bowman & Azzalini (1997) Applied Smoothing Techniques for DataAnalysis. We use a subset of this, namely obeservations 2, 22, 42, 62, 82, 102, 122, 142, 162,182, 202 and 222. We only use a subset otherwise some plots become too crowded so it is fordisplay purposes only.) The data points are represented by crosses on the x-axis.
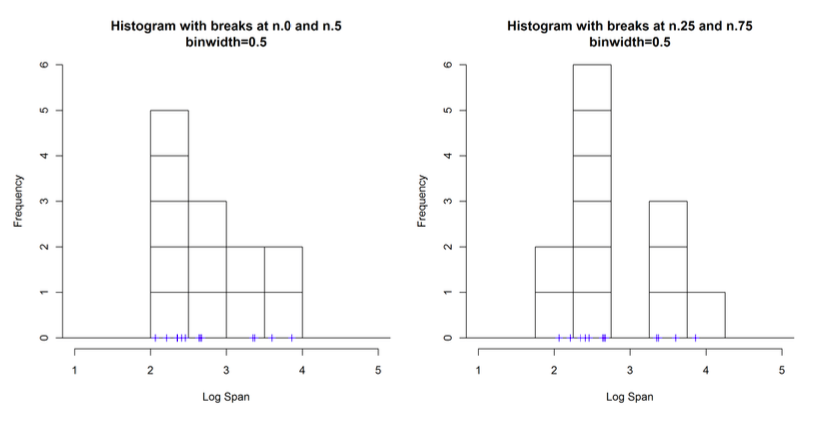
If we choose breaks at 0 and 0.5 and a binwidth of 0.5, the our histogram looks like the oneon top. It appears that the this density is unimodal and skewed to the right, according tothis histogram on the left. The choice of end points has a particularly marked effect of theshape of a histogram. For example if we use the same binwidth but with the end pointsshifted up to 0.25 and 0.75, then out histogram looks like this one below. We now have acompletely different estimate of the density – it now appears to be bimodal.
We have illustrated the properties of histograms with these two examples: they are
• not smooth
• depend on end points of bins
• depend on width of bins.
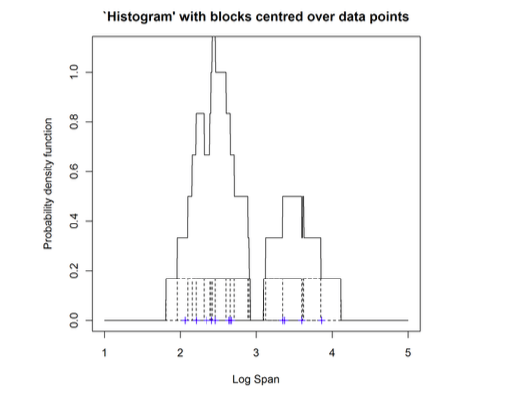
We can alleviate the first two problems by using kernel density estimators. To remove thedependence on the end points of the bins, we centre each of the blocks at each data pointrather than fixing the end points of the blocks.
In the above ‘histogram’, we place a block of width 1/2 and height 1/6 (the dotted boxes)as there are 12 data points, and then add them up. This density estimate (the solid curve)is less blocky than either of the histograms, as we are starting to extract some of the finerstructure. It suggests that the density is bimodal.
This is known as box kernel density estimate – it is still discontinuous as we have used adiscontinuous kernel as our building block. If we use a smooth kernel for our building block,then we will have a smooth density estimate. Thus we can eliminate the first problem withhistograms as well. Unfortunately we still can’t remove the dependence on the bandwidth(which is the equivalent to a histogram’s binwidth).
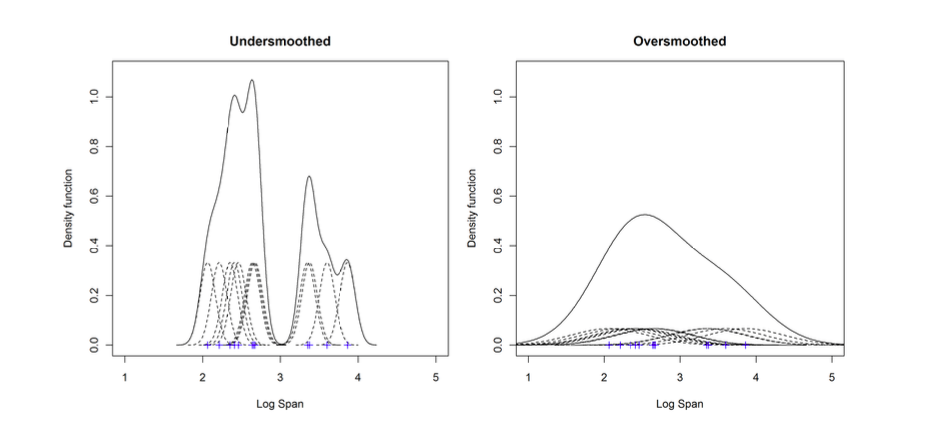
It’s important to choose the most appropriate bandwidth as a value that is too small ortoo large is not useful. If we use a normal (Gaussian) kernel with bandwidth or standarddeviation of 0.1 (which has area 1/12 under the each curve) then the kernel density estimateis said to undersmoothed as the bandwidth is too small in the figure below. It appears thatthere are 4 modes in this density - some of these are surely artifices of the data. We cantry to eliminate these artifices by increasing the bandwidth of the normal kernels to 0.5. Weobtain a much flatter estimate with only one mode. This situation is said to be oversmoothedas we have chosen a bandwidth that is too large and have obscured most of the structure ofthe data.
So how do we choose the optimal bandwidth? A common way is the use the bandwidth thatminimises the optimality criterion (which is a function of the optimal bandwidth) AMISE =Asymptotic Mean Integrated Squared Error so then optimal bandwidth = argmin AMISEi.e. the optimal bandwidth is the argument that minimises the AMISE.
In general, the AMISE still depends of the true underlying density (which of course we don’thave!) and so we need to estimate the AMISE from our data as well. This means that thechosen bandwidth is an estimate of an asymptotic approximation. It now sounds as if it’s toofar away from the true optimal value but it turns out that this particular choice of bandwidthrecovers all the important features whilst maintaining smoothness.
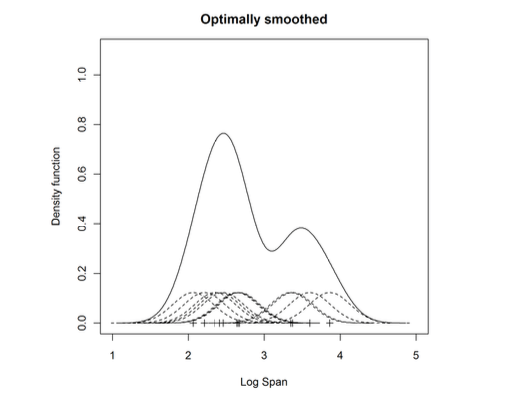
The optimal value of the bandwidth for our dataset is about 0.25. From the optimallysmoothed kernel density estimate, there are two modes. As these are the log of aircraft wingspan, it means that there were a group of smaller, lighter planes built, and these are clusteredaround 2.5 (which is about 12 m). Whereas the larger planes, maybe using jet engines asthese used on a commercial scale from about the 1960s, are grouped around 3.5 (about 33m).
The properties of kernel density estimators are, as compared to histograms:
• smooth
• no end points
• depend on bandwidth.
This has been a quick introduction to kernel density estimation. The current state of researchis that most of the issues concerning one-dimensional problems have been resolved. The nextstage is then to extend these ideas to the multi-dimensional case where much less researchhas been done. This is due to that there are the orientation of multi-dimensional kernels hasa large effect on the resulting density estimate (which has no counterpart in one-dimensionalkernels). I am currently looking for reliable methods for bandwidth selection for multivariatekernels. Some progress that I have made in plug-in methods is here. However this page ismore technical and uses equations!
These notes are an edited version of a seminar given by Tarn Duong on 24 May 2001 aspart of the Weatherburn Lecture Series for the Department of Mathematics and Statis-tics, at the University of Western Australia. Please feel free to contact the author attarn(dot)duong(at)gmail(dot)com if you have any questions. Tarn’s web page contains moredetails of his research into kernel smoothing methods.
4





















 370
370











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








