DARTS

DARTS

Related Work

传统的NAS的方法：

1.基于强化学习的NAS

2.基于进化学习的NAS

现存优化传统NAS的方法：

1.搜索空间的特殊结构

2.单个结构的权重或者性能的预测

3.多个结构之间的权值共享

可以应用于NAS上的传统优化方法

1.强化学习

2.进化学习

3.MCTS

4.SMBO

5.Bayesian Optimization

以上方法并不能Work的原因在于：NAS是一种基于离散空间上的黑盒优化过程，因此在过多的结构搜索中，存在着过多的结构性能评估的过程

Motivation

Tips 1: Search Space

很多现存的NAS的搜索空间是离散的，因此本文将搜索空间弱化为一个连续的空间结构，以此可以使用梯度夏下降进行性能优化,DARTS能够在丰富的搜索空间中搜索到一种具有复杂图形拓扑结构的高性能框架

• Search Space 的连续性并不是首创的方法，但是Darts与传统的方法不同的是，传统的方法是在一个连续搜索空间中，搜索一种特殊的结构(Filters Shape、Branch Pattern)，而DARTS是搜索一种完整的网络结构

Method

Search Space

目标：搜索一种Convolutional Cell(有向无环图，其中包含$N$个节点-Feature Map,有向边是一种对Feature Map进行转换的的相互关联的操作)作为网络最终结构的Building Block，得到的Cell既可以通过Stack成Classification network，也可以循环连接形成Recurrent Network

细节：

• Class Cell: Cell的输入对应其上一层的输出

• Recurrent Cell: 当前的输入State是前一步运算过后的State

• Cell 的总输出:在所有网络结构内部的Nodes进行Reduction Operation(e.g. Concatenation)
  $$x^i=\underset{j<i}{\Sigma }{o}^{(i,j)}{x}^{(j)}$$

• 为了表示某些节点之间是没有任何联系的，因此此处引入了**$Zero-Operation$**

Continuous Relaxation Scheme

目的：能够在Architecture和Weight两者的联合优化问题上能够学到一个可微的目标

具体实现：为了能够使得搜索空间连续，我们将特殊操作的类别选择简化成对于所有可能的Operations的Softmax
$${\stackrel{-}{o}}^{(i,j)}(x)=\underset{(o\in O)}{\Sigma }\frac{exp({\alpha }_o^{(i,j)})}{\Sigma (o^{{}^{\prime }}\in O)({{\alpha }_o^{{}^{\prime }}}^{(i,j)})}$$

• [说明]

  • 成对Nodes之间混合权重的操作被向量${\alpha }^{i,j}\in |\mathbb{O}|$进行参数化，此时的结构化搜索被简化成学习一系列连续的变量 α = { α ( i , j ) } \alpha=\{\alpha^{(i,j)}\} α={α(i,j)}的过程

  • 在搜索过程的最后，通过利用最大可能替换的方式，得到最终的网络结构
    $$o^{(i,j)}=\underset{o\in O}{\mathrm{argmax}}{\alpha }_o^{(i,j)}$$

  • 同样利用了Reward机制，DARTS将Validation Performance 当作自己的Reward

方法目标——Bilevel Optimization：

• ${\alpha }^{\ast }$: [Upper-Level] 找到一个合适的${\alpha }^{\ast }$来最小化$L_{val}(w^{\ast },{\alpha }^{\ast })$

• $w^{\ast }$:[Lower-Level] 找到合适的权重来最小化训练Loss,$L_{train}(w,{\alpha }^{\ast })$
  KaTeX parse error: Expected group after '_' at position 98: …\mathop{argmin}_̲\limits{w}\quad…

Approximation

**具体内容:**使得$w,\alpha$能够在各自的搜索空间中，分别利用梯度下降法进行交错优化

$\alpha$的优化问题：
$${\nabla }_{\alpha }{L}_{val}(w^{{}^{\prime }},\alpha )-\xi {\nabla }_{\alpha ,w}^2{L}_{train}(w,\alpha ){\nabla }_{w^{{}^{\prime }}}{L}_{val}(w^{{}^{\prime }},\alpha )$$

$$w^{{}^{\prime }}=w-\xi {\nabla }_w{L}_{train}(w,\alpha )$$

• 一阶近似：$\xi =0$，此时，基于结构的二阶导消失，也即：$\alpha$与$weight$之间相互独立，实验证明，其效果比较差

• 二阶近似：$\xi >0$，与一阶近似相反，其效果比较好

  作者通过特例的收敛效果图来解释了一下学习率对于网络收敛性的影响，如下图所示

Tips：在(5)式中，后面一项是利用了矩阵乘法运算，因此本文利用了有限差分方法进行计算上的近似运算
$${\nabla }_{\alpha ,w}^2{L}_{train}(w,\alpha ){\nabla }_{w^{{}^{\prime }}}{L}_{val}(w^{{}^{\prime }},\alpha )\approx \frac{{\nabla }_{\alpha }{L}_{train}(w^{+},\alpha )-{\nabla }_{\alpha }{L}_{t}rain(w^{-},\alpha )}{2ϵ}$$

$$\begin{gathered} w^{+}=w+ϵ{\nabla }_{w^{{}^{\prime }}}{L}_{val}(w^{{}^{\prime }},\alpha ) \\ {w}^{-}=w-ϵ{\nabla }_{w^{{}^{\prime }}}{L}_{val}(w^{{}^{\prime }},\alpha ) \end{gathered}$$

Deriving Discrete Architectures

Step 1:为每一个中间节点保留$k$个强有力的先驱，统计计算边上的可选的操作，Convolutional Cell中$k=2$，Recurrent Cell中$k=1$

**Step 2:**通过$argmax$的操作选择最有效的边上的Optimation

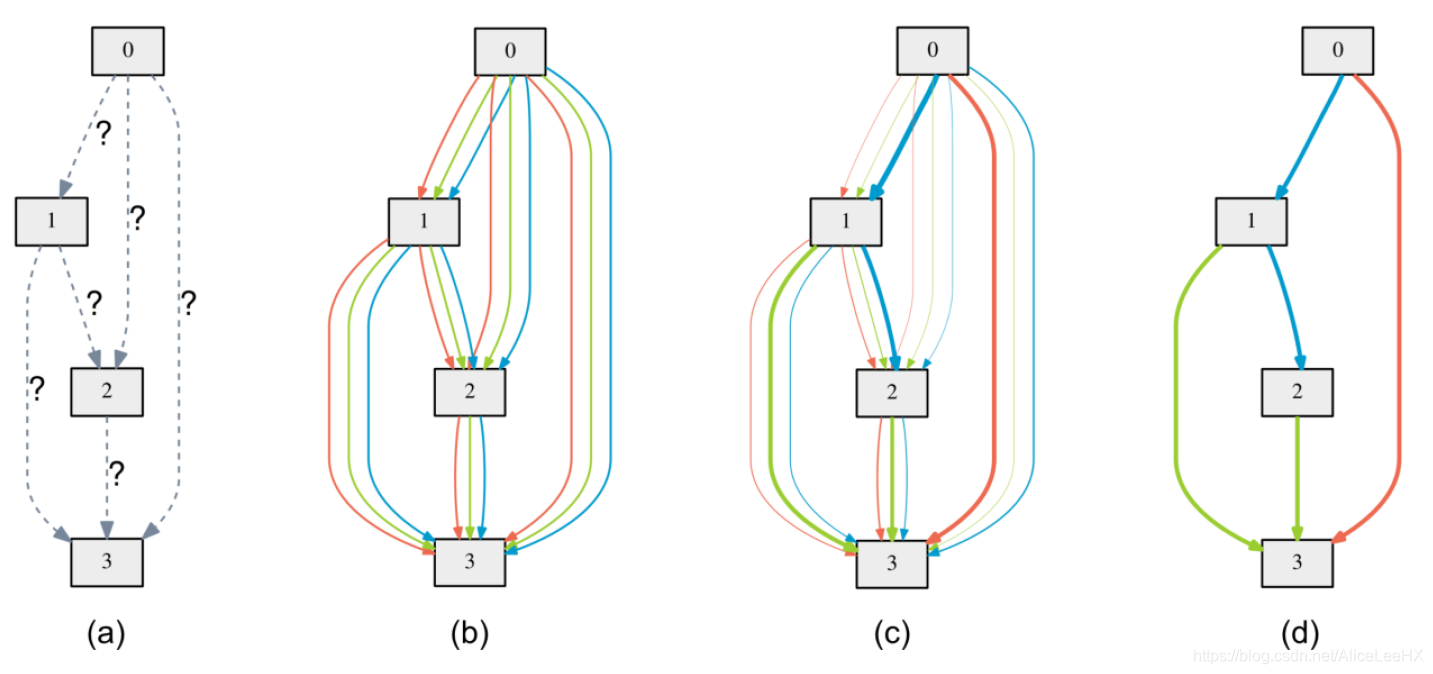
a:初始化Nodes，其中，两点之间的操作是不可知的

b:通过在每个边上混合操作生成一个连续的可选的操作空间

c:通过解决Bilevel的优化问题，联合优化混合操作概率和权重

d:从混合操作概率中得到最终的网络结构

搜索空间预定义：

Optimations:

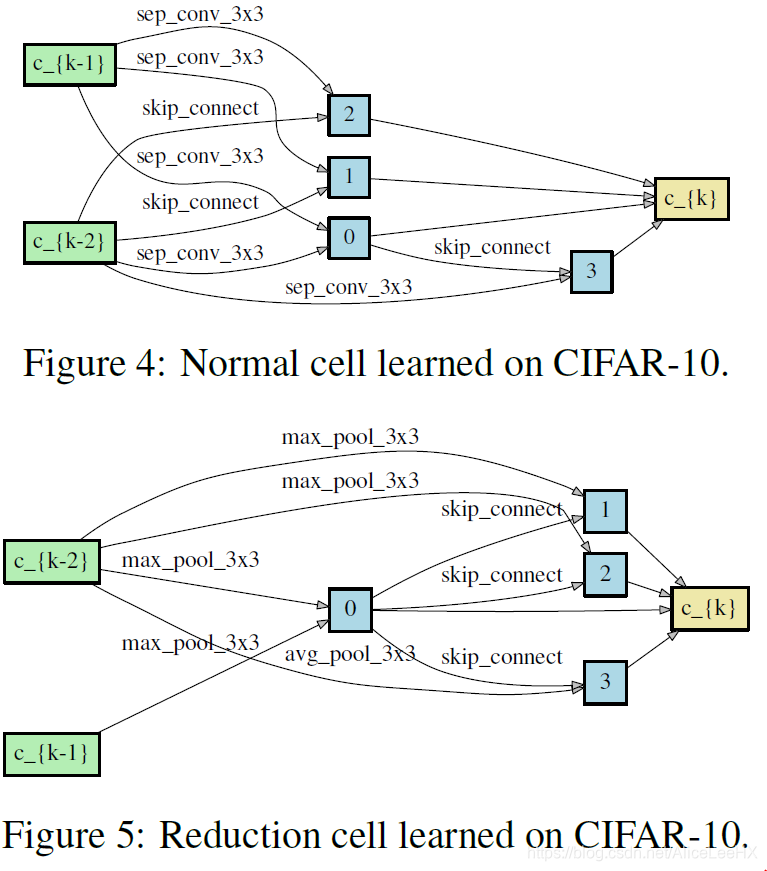
[Normal]

separable convolutions	dilated convolutions	max pooling	average pooling	Identity	Zero
$3\times 3$、$5\times 5$	$3\times 3$、$5\times 5$	$3\times 3$	$3\times 3$

• 以上所有操作的Stride均设置为1，同时还带有Padding操作
• 使用了$ReLU-Conv-BN$为顺序的卷积操作，每一个Separable Convolution均利用两次这样的顺序结构

Cell:

• 每个Cell包含7个Nodes
• Nodes的输出定义为所有中间Nodes(除输入)的结果的Depthwise Concatenate
• 第$k$个Cell的第一个输入对应于第$k-2$个Cell的输出，第$k$个Cell的第二个输入对应于第$k-1$个Cell的输出
• Network是将得到的Cell进行Stack组成

[Reduce]

在网络总深度的$\frac{1}{3}$和$\frac{2}{3}$处Reduction Cell(e.g. Concatenat),同时在Reduce Cell中，除了引入上面所有的操作以外，还使用了$1\times 1$卷积，Cell中所有的靠近输入节点的操作的Stride均设为2

Experience