源自:http://blog.csdn.net/chuan6099/article/details/8952978
动态规划法
经常会遇到复杂问题不能简单地分解成几个子问题,而会分解出一系列的子问题。简单地采用把大问题分解成子问题,并综合子问题的解导出大问题的解的方法,问题求解耗时会按问题规模呈幂级数增加。
为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组中,这就是动态规划法所采用的基本方法。
【问题】 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题,设A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”为它们的最长公共子序列。不难证明有以下性质:
(1) 如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
(2) 如果am-1!=bn-1,则若zk-1!=am-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列;
(3) 如果am-1!=bn-1,则若zk-1!=bn-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有am-1=bn-1,则进一步解决一个子问题,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一个最长公共子序列;如果am-1!=bn-1,则要解决两个子问题,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
求解:
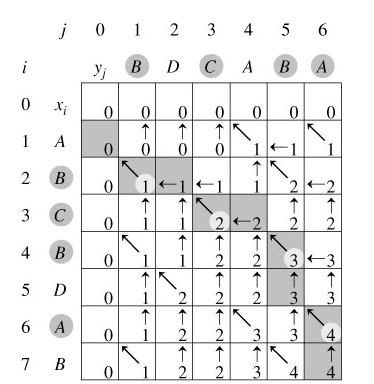
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
问题的递归式写成:
回溯输出最长公共子序列过程:
算法分析:
由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m + n)。
- #include <stdio.h>
- #include <string.h>
- #define MAXLEN 100
- void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN]) {
- int i, j;
- for(i = 0; i <= m; i++)
- c[i][0] = 0;
- for(j = 1; j <= n; j++)
- c[0][j] = 0;
- for(i = 1; i<= m; i++) {
- for(j = 1; j <= n; j++) {
- if(x[i-1] == y[j-1]) {
- c[i][j] = c[i-1][j-1] + 1;
- b[i][j] = 0;
- } else if(c[i-1][j] >= c[i][j-1]) {
- c[i][j] = c[i-1][j];
- b[i][j] = 1;
- } else {
- c[i][j] = c[i][j-1];
- b[i][j] = -1;
- }
- }
- }
- }
- void PrintLCS(int b[][MAXLEN], char *x, int i, int j) {
- if(i == 0 || j == 0)
- return;
- if(b[i][j] == 0) {
- PrintLCS(b, x, i-1, j-1);
- printf("%c ", x[i-1]);
- } else if(b[i][j] == 1)
- PrintLCS(b, x, i-1, j);
- else
- PrintLCS(b, x, i, j-1);
- }
- int main(int argc, char **argv) {
- char x[MAXLEN] = {"ABCBDAB"};
- char y[MAXLEN] = {"BDCABA"};
- int b[MAXLEN][MAXLEN];
- int c[MAXLEN][MAXLEN];
- int m, n;
- m = strlen(x);
- n = strlen(y);
- LCSLength(x, y, m, n, c, b);
- PrintLCS(b, x, m, n);
- return 0;
- }
//Reference:http://www.ahathinking.com/archives/124.html
使用动态规划求解这个问题,先寻找最优子结构。设X=<x1,x2,…,xm>和Y=<y1,y2,…,yn>为两个序列,LCS(X,Y)表示X和Y的一个最长公共子序列,可以看出 如果xm=yn,则LCS ( X,Y ) = xm + LCS ( Xm-1,Yn-1 )。 如果xm!=yn,则LCS( X,Y )= max{ LCS ( Xm-1, Y ), LCS ( X, Yn-1 ) } LCS问题也具有重叠子问题性质:为找出X和Y的一个LCS,可能需要找X和Yn-1的一个LCS以及Xm-1和Y的一个LCS。但这两个子问题都包含着找Xm-1和Yn-1的一个LCS,等等. DP最终处理的还是数值(极值做最优解),找到了最优值,就找到了最优方案;为了找到最长的LCS,我们定义dp[i][j]记录序列LCS的长度,合法状态的初始值为当序列X的长度为0或Y的长度为0,公共子序列LCS长度为0,即dp[i][j]=0,所以用i和j分别表示序列X的长度和序列Y的长度,状态转移方程为 dp[i][j] = 0 如果i=0或j=0 dp[i][j] = dp[i-1][j-1] + 1 如果X[i-1] = Y[i-1] dp[i][j] = max{ dp[i-1][j], dp[i][j-1] } 如果X[i-1] != Y[i-1]
#include <iostream>
using namespace std;
/* LCS
* 设序列长度都不超过20
*/
int dp[21][21]; /* 存储LCS长度, 下标i,j表示序列X,Y长度 */
int i, j;
void main()
{
char *strX = "ABCBDAB";
char *strY = "BDCABA";
int xlen = strlen(strX);
int ylen = strlen(strY);
/* dp[0-xlen][0] & dp[0][0-ylen] 都已初始化0 */
for(i = 1; i <= xlen; ++i)
{
for(j = 1; j <= ylen; ++j)
{
if(strX[i-1] == strY[j-1])
{
dp[i][j] = dp[i-1][j-1] + 1;
}else if(dp[i][j-1] > dp[i-1][j])
{
dp[i][j] = dp[i][j-1];
}else
{
dp[i][j] = dp[i-1][j];
}
}
}
printf("len of LCS is: %d\n", dp[xlen][ylen]);
/* 输出LCS 本来是逆序打印的,可以写一递归函数完成正序打印
这里采用的方法是将Y作为临时存储LCS的数组,最后输出Y
*/
i = xlen;
j = ylen;
int k = dp[i][j];
char lcs[21] = {'\0'};
while(i && j)
{
if(strX[i-1] == strY[j-1] && dp[i][j] == dp[i-1][j-1] + 1)
{
lcs[--k] = strX[i-1];
--i; --j;
}else if(strX[i-1] != strY[j-1] && dp[i-1][j] > dp[i][j-1])
{
--i;
}else
{
--j;
}
}
printf("%s\n",lcs);
}
2)最长公共子串(Longest-Common-Substring,LCS)
这里要求是需要连续,子串需要连续,子序列不需要连续。
既然需要连续,那问题就相对要简单点。
我们使用dp[i][j]表示 以x[i]和y[j]结尾的最长公共子串的长度,因为要求子串连续,所以对于X[i]与Y[j]来讲,它们要么与之前的公共子串构成新的公共子串;要么就是不构成公共子串。故状态转移方程
- X[i] == Y[j],dp[i][j] = dp[i-1][j-1] + 1
- X[i] != Y[j],dp[i][j] = 0
对于初始化,i==0或者j==0,如果X[i] == Y[j],dp[i][j] = 1;否则dp[i][j] = 0。
#include <stdio.h>
#include <string>
/* 最长公共子串 DP */
int dp[30][30];
int maxlen, maxindex;
void outputLCS(char * X);
void LCS_dp(char * X, int xlen, char * Y, int ylen)
{
maxlen = maxindex = 0;
for(int i = 0; i < xlen; ++i)
{
for(int j = 0; j < ylen; ++j)
{
if(X[i] == Y[j])
{
if(i && j)
{
dp[i][j] = dp[i-1][j-1] + 1;
}
if(i == 0 || j == 0)
{
dp[i][j] = 1;
}
if(dp[i][j] > maxlen)
{
maxlen = dp[i][j];
maxindex = i + 1 - maxlen;
}
}
}
}
outputLCS(X);
}
void outputLCS(char * X)
{
if(maxlen == 0)
{
printf("NULL LCS\n");
return;
}
printf("The len of LCS is %d\n",maxlen);
int i = maxindex;
while(maxlen--)
{
printf("%c",X[i++]);
}
printf("\n");
}
void main()
{
char X[] = "aaaba";
char Y[] = "abaa";
/* DP算法 */
LCS_dp(X,strlen(X),Y,strlen(Y));
}
基本算法使用Hash
要求子串中的字符不能重复,判重问题首先想到的就是hash,寻找满足要求的子串,最直接的方法就是遍历每个字符起始的子串,辅助hash,寻求最长的不重复子串,由于要遍历每个子串故复杂度为O(n^2),n为字符串的长度,辅助的空间为常数hash[256]。代码如下:
/* 最长不重复子串 设串不超过30
* 我们记为 LNRS
*/
int maxlen;
int maxindex;
void output(char * arr);
/* LNRS 基本算法 hash */
char visit[256];
void LNRS_hash(char * arr, int size)
{
for(int i = 0; i < size; ++i)
{
memset(visit,0,sizeof(visit));
visit[arr[i]] = 1;
for(int j = i+1; j < size; ++j)
{
if(visit[arr[j]] == 0)
{
visit[arr[j]] = 1;
}else
{
if(j-i > maxlen)
{
maxlen = j - i;
maxindex = i;
}
break;
}
}
}
output(arr);
}DP方案
前面刚刚讨论过最长递增子序列的问题,咋一想就觉得二者有点类似,何不向DP方面想一下,为什么说二者类似,在LIS问题中,对于当前的元素,要么是与前面的LIS构成新的最长递增子序列,要么就是与前面稍短的子序列构成新的子序列或单独构成新子序列;
同理,对于最长不重复子串,某个当前的字符,如果它与前面的最长不重复子串中的字符没有重复,那么就可以以它为结尾构成新的最长子串;如果有重复,那么就与某个稍短的子串构成新的子串或者单独成一个新子串。
举个例子:例如字符串“abcdeab”,第二个字符a之前的最长不重复子串是“abcde”,a与最长子串中的字符有重复,但是它与稍短的“bcde”串没有重复,于是它可以与其构成一个新的子串,之前的最长不重复子串“abcde”结束;
再看一个例子:字符串“abcb”,跟前面类似,最长串“abc”结束,第二个字符b与稍短的串“c”构成新的串;
这两个例子,可以看出些眉目:当一个最长子串结束时(即遇到重复的字符),新的子串的长度是与(第一个重复的字符)的下标有关的。
于是类似LIS,对于每个当前的元素,我们“回头”去查询是否有与之重复的,如没有,则最长不重复子串长度+1,如有,则是与第一个重复的字符之后的串构成新的最长不重复子串,新串的长度便是当前元素下标与重复元素下标之差。
于是我们得到O(N^2)的DP方案,我们可以与LIS的DP方案进行对比,是一个道理的。代码如下:
/* LNRS dp */
int dp[30];
void LNRS_dp(char * arr, int size)
{
int i, j;
maxlen = maxindex = 0;
dp[0] = 1;
for(i = 1; i < size; ++i)
{
for(j = i-1; j >= 0; --j)
{
if(arr[j] == arr[i])
{
dp[i] = i - j;
break;
}
}
if(j == -1)
{
dp[i] = dp[i-1] + 1;
}
if(dp[i] > maxlen)
{
maxlen = dp[i];
maxindex = i + 1 - maxlen;
}
}
output(arr);
}DP + Hash方案
上面的DP方案是O(n^2)的,之所以是n^2,是因为“回头”去寻找重复元素的位置了,受启发于最初的Hash思路,我们可以用hash记录元素是否出现过,我们当然也可以用hash记录元素出现过的下标,既然这样,在DP方案中,我们何不hash记录重复元素的位置,这样就不必“回头”了,而时间复杂度必然降为O(N),只不过需要一个辅助的常数空间visit[256],典型的空间换时间。
代码如下:这样遍历一遍便可以找到最长不重复子串
/* LNRS dp + hash 记录下标 */
void LNRS_dp_hash(char * arr, int size)
{
memset(visit, -1, sizeof visit); //visit数组是-1的时候代表这个字符没有在集合中
memset(dp, 0, sizeof dp);
maxlen = maxindex = 0;
dp[0] = 1;
visit[arr[0]] = 0;
for(int i = 1; i < size; ++i)
{
if(visit[arr[i]] == -1) //表示arr[i]这个字符以前不存在
{
dp[i] = dp[i-1] + 1;
visit[arr[i]] = i; /* 记录字符下标 */
}else
{
dp[i] = i - visit[arr[i]];
}
if(dp[i] > maxlen)
{
maxlen = dp[i];
maxindex = i + 1 - maxlen;
}
}
output(arr);
}DP + Hash优化方案
写到这里,还是有些别扭,因为辅助的空间多了,是不是还能优化,仔细看DP最优子问题解的更新方程:
| 1 | |
dp[i-1]不就是更新dp[i]当前的最优解么?这与最大子数组和问题的优化几乎同出一辙,我们不需要O(n)的辅助空间去存储子问题的最优解,而只需O(1)的空间就可以了,至此,我们找到了时间复杂度O(N),辅助空间为O(1)(一个额外变量与256大小的散列表)的算法,代码如下
/* LNRS dp + hash 优化 */
void LNRS_dp_hash_impro(char * arr, int size)
{
memset(visit, -1, sizeof visit);
maxlen = maxindex = 0;
visit[arr[0]] = 0;
int curlen = 1;
for(int i = 1; i < size; ++i)
{
if(visit[arr[i]] == -1)
{
++curlen;
visit[arr[i]] = i; /* 记录字符下标 */
}else
{
curlen = i - visit[arr[i]];
}
if(curlen > maxlen)
{
maxlen = curlen;
maxindex = i + 1 - maxlen;
}
}
output(arr);
}最后给出输出函数与测试用例:
/* 输出LNRS */
void output(char * arr)
{
if(maxlen == 0)
{
printf("NO LNRS\n");
}
printf("The len of LNRS is %d\n",maxlen);
int i = maxindex;
while(maxlen--)
{
printf("%c",arr[i++]);
}
printf("\n");
}
void main()
{
char arr[] = "abcdeab";
/* LNRS 基本算法 */
LNRS_hash(arr,strlen(arr));
/* LNRS dp */
LNRS_dp(arr,strlen(arr));
/* LNRS dp + hash 记录下标 */
LNRS_dp_hash(arr,strlen(arr));
/* LNRS dp + hash 优化方案 */
LNRS_dp_hash_impro(arr,strlen(arr));
}4)最长递增子序列
第i个元素之前的最长递增子序列的长度要么是1(单独成一个序列),要么就是第i-1个元素之前的最长递增子序列加1,可以有状态方程:
LIS[i] = max{1,LIS[k]+1},其中,对于任意的k<=i-1,arr[i] > arr[k],这样arr[i]才能在arr[k]的基础上构成一个新的递增子序列。
#include <iostream>
using namespace std;
/* 最长递增子序列 LIS
* 设数组长度不超过 30
* DP
*/
int dp[31]; /* dp[i]记录到[0,i]数组的LIS */
int lis = 0; /* LIS 长度 */
int LIS(int * arr, int size)
{
for(int i = 0; i < size; ++i)
{
dp[i] = 1;
for(int j = 0; j < i; ++j)
{
if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
{
dp[i] = dp[j] + 1;
if(dp[i] > lis)
{
lis = dp[i];
}
}
}
}
return lis;
}
/* 输出LIS */
void outputLIS(int * arr, int index)
{
bool isLIS = 0;
if(index < 0 || lis == 0)
{
return;
}
if(dp[index] == lis)
{
--lis;
isLIS = 1;
}
outputLIS(arr,--index);
if(isLIS)
{
printf("%d ",arr[index+1]);
}
}
void main()
{
//int arr[] = {1,-1,2,-3,4,-5,6,-7};
int arr[] = { 9, 3, 8, 11, 4, 5, 6, 4, 19, 6, 1, 7 };
/* 输出LIS长度; sizeof 计算数组长度 */
printf("%d\n",LIS(arr,sizeof(arr)/sizeof(int)));
/* 输出LIS */
outputLIS(arr,sizeof(arr)/sizeof(int) - 1);
printf("\n");
int i = 0;
while (i < sizeof(arr)/sizeof(int) && dp[i] != 0)
{
cout << dp[i] << ' ';
i++;
}
cout << endl;
char *c = "asdfasdf";
cout << strlen(c) << endl;
}注:
有递增子序列,就相对的有递减或者非递增序列(即递减序列中有相等)
有这么一个题,http://acm.uestc.edu.cn/problem.php?pid=1308
思想是一样的,需要改动就是判断条件,
取dp[i]表示第i个拦截导弹拦截的是第几个袭击导弹,
dp[i] = max{1,dp[j] + 1},1<j<i<n
include<stdio.h>
int main()
{
int n,i,j,num,h[1000],max[1000];
while(~scanf("%d",&n))
{
num=0;
for(i=0;i<n;++i)
{
scanf("%d",&h[i]);
max[i]=1;
}
for(i=1;i<n;++i)
{ for(j=0;j<i;++j)
{
if(h[j]<=h[i]&&max[j]+1>max[i])
max[i]=max[j]+1;
if(num<max[i])
num=max[i];
}
printf("%d\n",num);
}
return 0;
}5)最长回文子串
DP的考虑源于暴力方法,暴力方法是寻找一个字符串的所有子串,需要O(n^2)的开销,然后对于每一个子串需要O(n)的开销来判断是否是回文,故暴力方案为O(n^3),但是这里有一个问题,就是在暴力的时候有重复判断;
例如,如果子串X为回文,那么sXs也是回文;如果X不是回文,那么sXs也不是回文;另外,ss也是回文。所以这里使用DP我们可以按照子串长度从小到大的顺序来构建DP状态数组,使用一个二维数组dp[i][j]记录子串[i-j]是否为回文子串,那么我们就有初始化和自底向上的方案了;
初始化:单字符串和相等的双字符串为回文
自底向上构造:X[i]==X[j] && dp[i+1][j-1]==1 则dp[i][j] = 1
#include <iostream>
using namespace std;
/* 最长回文子串 LPS - DP */
int maxlen; // LPS长度
/* DP解法 */
bool dp[31][31]; // dp[i][j]记录子串[i-j]是否构成回文
void LPS_dp(char * X, int xlen) // 略去测试X合法性
{
maxlen = 1;
for(int i = 0; i < xlen; ++i) // 初始化
{
dp[i][i] = 1; // 单字符为回文
if(i && (X[i-1] == X[i]))
{
dp[i-1][i] = 1; // 双字符串为回文
}
}
for(int len = 2; len < xlen; ++len)
{
for(int begin = 0; begin < xlen-len; ++begin)
{
int end = begin + len; // 从长度为3开始
if((X[begin]==X[end]) && (dp[begin+1][end-1]==1))
{
dp[begin][end] = 1;
if(end - begin + 1 > maxlen)
{
maxlen = end - begin + 1;
}
}
}
}
}











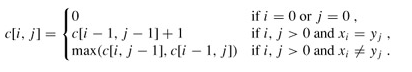














 730
730

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








