http://zh.wikipedia.org/wiki/RSA加密演算法
公钥和私钥的产生
假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥:
- 随意选择两个大的质数p和q,p不等于q,计算N=pq。
- 根据欧拉函数,不大于N且与N互质的整数个数为(p-1)(q-1)
- 选择一个整数e与(p-1)(q-1)互质,并且e小于(p-1)(q-1)
- 用以下这个公式计算d:d× e ≡ 1 (mod (p-1)(q-1))
- 将p和q的记录销毁。
e是公钥,d是私钥。d是秘密的,而N是公众都知道的。Alice将她的公钥传给Bob,而将她的私钥藏起来。
加密消息
假设Bob想给Alice送一个消息m,他知道Alice产生的N和e。他使用起先与Alice约好的格式将m转换为一个小于N的整数n,比如他可以将每一个字转换为这个字的Unicode码,然后将这些数字连在一起组成一个数字。假如他的信息非常长的话,他可以将这个信息分为几段,然后将每一段转换为n。用下面这个公式他可以将n加密为c:
计算c并不复杂。Bob算出c后就可以将它传递给Alice。
解密消息
Alice得到Bob的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n:
得到n后,她可以将原来的信息m重新复原。
解码的原理是
以及ed ≡ 1 (mod p-1)和ed ≡ 1 (mod q-1)。费马小定理证明
-
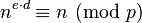 和
和
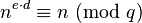
这说明(因为p和q是不同的质数)









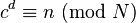

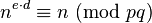














 5976
5976

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








