数独算法-递归与回溯

最新推荐文章于 2024-08-06 16:10:04 发布

bacouhuai7918

最新推荐文章于 2024-08-06 16:10:04 发布

阅读量319

点赞数

文章标签： java 数据结构与算法人工智能

原文链接：http://www.cnblogs.com/yhtboke/p/5749139.html

版权

1.概述

数独（Sudoku）是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-9，不重复。
1)终盘数量:
数独中的数字排列千变万化，那么究竟有多少种终盘的数字组合呢？
6,670,903,752,021,072,936,960（约为6.67×10的21次方）种组合，2005年由Bertram Felgenhauer和Frazer Jarvis计算出该数字，并将计算方法发布在他们网站上，如果将等价终盘（如旋转、翻转、行行对换，数字对换等变形）不计算，则有5,472,730,538个组合。数独终盘的组合数量都如此惊人，那么数独题目数量就更加不计其数了，因为每个数独终盘又可以制作出无数道合格的数独题目。
2)标准数独:
目前（截止2011年）发现的最少提示数9×9标准数独为17个提示，截止2011年11月24日16:14，共发现了非等价17提示数谜题49151题，此数量仍在缓慢上升中，如果你先发现了17提示数的题目，可以上传至“17格数独验证”网站，当然你也可以在这里下载这49151题。
Gary McGuire的团队在2009年设计了新的算法，利用Deadly Pattern的思路，花费710万小时CPU时间后，于2012年1月1日提出了9×9标准数独不存在16提示唯一解的证明，继而说明最少需要17个提示数。并将他们的论文以及源代码更新在2009年的页面上。

以上内容来自于百度百科。

2.算法实现（Java）

网络上有很多解数独的算法，例如舞蹈链算法、遗传算法等。参考各种算法的性能比较：
递归回溯对数独情有独钟。
本文解数独用的是候选数法（人工选择）+万能搜索法，搜索+剪枝（递归+回溯），参考博文：
数独算法及源代码

1）未优化的算法-只有递归回溯（单解或多解）

从第一个位置开始依次检索所有格子（暴力），执行时间会比较长。
多解与单解：很简单，在找到解的语句返回false表示继续递归寻解，返回true表示停止寻解（不会复位，不回溯）

package com.sudoku;

import java.util.Date;


public class Sudoku {
    private int[][] matrix = new int[9][9];//注意下标从0开始 private int count=0;//解的数量 private int maxCount = 1;//解的最大数量 //输入格式要求0作为占位符(表示待填)，只接受数字字符串，长度为81位 public Sudoku(String input,int maxCount) throws Exception{ if(input==null||input.length()!=81||!input.matches("[0-9]+")) throw new Exception("必须为81位长度的纯数字字符串"); init(input); this.maxCount = maxCount; } public Sudoku(String input) throws Exception{ this(input,1); } public Sudoku(){ } public int getCount(){ return count; } //初始化数独 private void init(String input){ for(int i=0;i<input.length();i++) { String s = input.substring(i, i+1); int value = Integer.parseInt(s); matrix[i/9][i%9]=value; } } //万能解题法的“搜索+剪枝”,递归与回溯 //从(i,j)位置开始搜索数独的解,i和j最大值为8 private boolean execute(int i,int j){ //寻找可填的位置（即空白格子），当前(i,j)可能为非空格，从当前位置当前行开始搜索 outer://此处用于结束下面的双层循环 for(int x=i;x<9;x++){ for(int y=0;y<9;y++){ if(matrix[x][y]==0){ i=x; j=y; break outer; } } } //如果从当前位置并未搜索到一个可填的空白格子，意味着所有格子都已填写完了，所以找到了解 if(matrix[i][j]!=0){ count++; System.out.println("第"+count+"种解:"); output(); if(count==maxCount) return true;//return true 表示只找寻一种解，false表示找所有解 else return false; } //试填k for(int k=1;k<=9;k++){ if(!check(i,j,k)) continue; matrix[i][j] = k;//填充 //System.out.println(String.format("(%d,%d,%d)",i,j,k)); if(i==8&&j==8) {//填的正好是最后一个格子则输出解 count++; System.out.println("第"+count+"种解:"); output(); if(count==maxCount) return true;//return true 表示只找寻一种解，false表示找所有解 else return false; } //计算下一个元素坐标，如果当前元素为行尾，则下一个元素为下一行的第一个位置（未填数）， //否则为当前行相对当前元素的下一位置 int nextRow = (j<9-1)?i:i+1; int nextCol = (j<9-1)?j+1:0; if(execute(nextRow,nextCol)) return true;//此处递归寻解，若未找到解，则返回此处,执行下面一条复位语句 //递归未找到解，表示当前(i,j)填k不成功，则继续往下执行复位操作，试填下一个数 matrix[i][j] = 0; } //1~9都试了 return false; } public void execute(){ execute(0,0);//从第一个位置开始递归寻解 } //数独规则约束，行列宫唯一性,检查(i,j)位置是否可以填k private boolean check(int i,int j,int k){ //行列约束,宫约束，对应宫的范围 起始值为(i/3*3,j/3*3),即宫的起始位置行列坐标只能取0,3,6 for(int index=0;index<9;index++){ if(matrix[i][index]==k) return false; if(matrix[index][j]==k) return false; if(matrix[i/3*3+index/3][j/3*3+index%3]==k) return false; } return true; } public void output(){ for(int i=0;i<9;i++){ for(int j=0;j<9;j++) System.out.print(matrix[i][j]); System.out.println(); } } public static void main(String[] args) { try { //Sudoku sudoku = new Sudoku("000000000000000012003045000000000036000000400570008000000100000000900020706000500"); Sudoku sudoku = new Sudoku("123456789456789123789123456234567891567891234891234567345000000000000000000000000",10); //Sudoku sudoku = new Sudoku(); sudoku.output(); Date begin = new Date(); sudoku.execute(); System.out.println("执行时间"+(new Date().getTime()-begin.getTime())+"ms"); if(sudoku.getCount()==0) System.out.println("未找到解"); } catch (Exception e) { e.printStackTrace(); } } }

执行效果：
原数独：

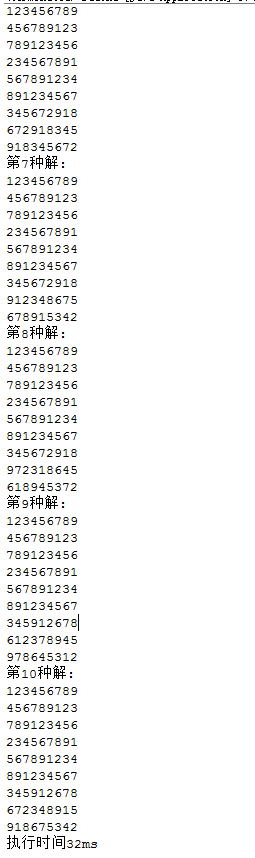
这里写图片描述

2）优化算法-添加（唯一法或唯余法、摒除法、三链数删减法）

由于前面一种未经过优化搜索条件，属于“暴力型”解法（Brute Force），若碰到需要递归非常大的空间时，消耗时间将是非常长的，还有可能会抛出内存溢出的异常。如果按照人的思维去解数独，绝对不会像计算机一样呆呆的一个一个地去试，相反，人工解数独首先考虑的是将候选数最少（通常为1，必填）的格子先肯定的填上去，各种方法都用尽后，所谓山穷水尽时才会考虑试填，（即计算机的运作方式：递归回溯），而试填时也是从最少的候选数的格子开始（通常为2），这样能有效的找到解，而计算机只能使用暴力。所以，在算法中加上人工智能选择的话，可以大大提高执行效率。
基本解题方法：隐性唯一解（Hidden Single）及显性唯一解（Naked Single），摒除法，余数法，候选数法
进阶解题方法：区块摒除法（Locked Candidates）、数组法（Subset）、四角对角线（X-Wing）、唯一矩形（Unique Rectangle）、全双值坟墓（Bivalue Universal Grave）、单数链（X-Chain）、异数链（XY-Chain）及其他数链的高级技巧等等。参考度娘：数独技巧

要仿照人工求解模式，需要采用候选数法对候选数进行删减法，其中可以应用到唯一（余）法，摒除法（行列宫）等。对应关系：
唯一（余）法：某个格子的候选数只剩下一个数字，则该数字必填如该格子。对应于唯一候选数法
摒除法：如果某个数字在某宫所有格子的所有候选数中总共只出现一次，则该数字必填入候选数包含它的那个格子中。行列情况同理。对应于隐性唯一候选数法。
三链数删减法:找出某一列、某一行或某一个九宫格中的某三个宫格候选数中，相异的数字不超过3个的情形，
进而将这3个数字自其它宫格的候选数中删减掉的方法就叫做三链数删减法。
这样程序执行流程是：

反复应用候选数删减法寻找必填项，直到候选数未发生变化（即找不到必填项了）
然后才递归寻解（如果上一步骤找到了解，那递归寻解只输出解了）

package com.sudoku;

import java.util.Date;
import java.util.HashSet;
import java.util.Set;

public class Sudoku {
    private int[][] matrix = new int[9][9];//注意下标从0开始 private String[][] candidature= new String[9][9];//表示候选数 private int count=0;//用于统计解的数量 private int maxCount = 1;//解的最大数量 //输入格式要求0作为占位符(表示待填)，只接受数字字符串，长度为81位 public Sudoku(String input,int maxCount) throws Exception{ if(input==null||input.length()!=81||!input.matches("[0-9]+")) throw new Exception("必须为81位长度的纯数字字符串"); init(input); output(); this.maxCount = maxCount<=0?1:maxCount; if(!isValid()) throw new Exception("无效数独(有数字重复)"); if(!initCandidature()) throw new Exception("不合格数独（无解数独）"); } public Sudoku(String input) throws Exception{ this(input,1); } public Sudoku(){ } public int getCount(){ return count; } //初始化数独和候选数 private void init(String input){ for(int i=0;i<input.length();i++) { String s = input.substring(i, i+1); int value = Integer.parseInt(s); matrix[i/9][i%9]=value; } } //校验给出的数独题目是否为有效数独（即某行列宫中有重复的数字则无效） private boolean isValid(){ Set<Integer> rowSet = new HashSet<Integer>(); Set<Integer> colSet = new HashSet<Integer>(); Set<Integer> gridSet = new HashSet<Integer>(); for(int x=0;x<9;x++){//对应于行列宫号，对应宫的起始位置为(x/3*3,x%3*3) 取余与乘除优先级相同 rowSet.clear(); colSet.clear(); gridSet.clear(); for(int index=0;index<9;index++){ if(matrix[x][index]>0&&!rowSet.add(matrix[x][index])){ //行重复 System.out.println(String.format("数独无效,第%d行重复！",x+1)); return false; } if(matrix[index][x]>0&&!colSet.add(matrix[index][x])){//列重复 System.out.println(String.format("数独无效,第%d列重复！",x+1)); return false; } if(matrix[x/3*3+index/3][x%3*3+index%3]>0&&!gridSet.add(matrix[x/3*3+index/3][x%3*3+index%3])){ System.out.println(String.format("数独无效,第%d宫重复！",x+1)); return false;//宫重复 } } } return true; } //初始化候选数(唯一法或唯余法),数独无解返回false private boolean initCandidature() throws Exception{ for(int i=0;i<9;i++){ for(int j=0;j<9;j++){ if(matrix[i][j]>0) continue; candidature[i][j]=""; for(int k=1;k<=9;k++){ if(check(i,j,k)) { candidature[i][j] += k; } } //如果待填格子候选数个数为0，不合格数独（无解数独） if(candidature[i][j]==null||candidature.length==0) { return false;//无解数独 } //候选数个数为1，对应于唯一法或唯余法，可以100%的将该候选数填入该格子中，并重新计算候选数 if(candidature[i][j].length()==1){ int k = Integer.parseInt(candidature[i][j]); matrix[i][j] = k; System.out.println(String.format("唯一(余)法必填项(%d,%d,%d)",i,j,k)); deleteCandidature(i,j,k); } //System.out.println(String.format("(%d,%d)",i,j)+"->"+candidature[i][j]); } } return true; } //删除(i,j)等位格群上的候选数k，当(i,j)上可以肯定的填入数字k时(等位格局包含除自身外共20个格子) //每次调用此方法后，候选数发生了变化，需要再次检查唯一（余）性质 //只要有一个候选数发生了删减，则返回true private boolean deleteCandidature(int i,int j,int k){ boolean change = false; for(int index=0;index<9;index++){ if(matrix[i][index]==0&&candidature[i][index]!=null&&candidature[i][index].contains(""+k)) { candidature[i][index] = candidature[i][index].replace(""+k,""); change = true; } if(matrix[index][j]==0&&candidature[index][j]!=null&&candidature[index][j].contains(""+k)){ candidature[index][j] = candidature[index][j].replace(""+k,""); change = true; } if(matrix[i/3*3+index/3][j/3*3+index%3]==0&&candidature[i/3*3+index/3][j/3*3+index%3]!=null &&candidature[i/3*3+index/3][j/3*3+index%3].contains(""+k)){ candidature[i/3*3+index/3][j/3*3+index%3] = candidature[i/3*3+index/3][j/3*3+index%3].replace(""+k,""); change = true; } } return change; } //唯一法或唯余法或唯一候选数法，检查每个格子候选数的个数是否为1 //此为最基础的方法、应用其他方法发生了删减候选数时都要应用此方法检查一遍 private boolean single(){ System.out.println("唯一法或唯余法:"); boolean change = false;//表示是否候选数是否发生变化(当有删除候选数操作时则发生了变化) for(int i=0;i<