初学线性分式变换(LFT)笔记

G.Jerry

已于 2024-12-20 16:36:17 修改

阅读量942

点赞数 5

文章标签：笔记

于 2024-12-20 16:30:39 首次发布

本文链接：https://blog.csdn.net/baolan2020/article/details/144595303

版权

## 定义

线性分式变换(Linear fractional transformation)是具有如下形式的函数：

$T(z)=\frac{az+b}{cz+d}$

其中， $a,b,c,d$ 是复常数，且有 $ad-bc \neq 0$ 。这也被称为莫比乌斯变换或双线性变换。

## 困惑

在这一部分记录我曾出现的困惑。

问题1：为什么有 $ab-cd \neq 0$ ？

解答1：

因为

$T(z) =\frac{az+b}{cz+d} =\frac{\frac{a}{b}z+1}{\frac{c}{d}z+1} \frac{b}{d}$

当 $ad-bc=0$ 时，有 $\frac{a}{b}=\frac{c}{d}$ 。所以，线性分式变换就会变成常函数，即

$T(z)=\frac{b}{d}$ ，

如果它是常函数的话，我们就没必要把它复杂化成线性分式变换来做工作了。

问题2：为什么要关注 $z \mapsto \infty$ 和 $T(z) \mapsto \infty$ 的情况？

解答2：

首先说明这两种情况分别是

$T(\infty)=\left\{\begin{matrix} \frac{a}{c}, \text{if} c \neq 0\\ \infty, \text{if} c=0 \end{matrix}\right.\\ T(-\frac{d}{c})=\infty, \text{if} c \neq 0$

它说 “定义这两种情况便于我们考虑在扩展复平面 $C \cup \left\{ \infty \right\}$ 上定义的线性变换” 。这句话将在后面的例子中解释。（我当时不能理解的地方在于：这个拓展复平面C在哪里？为什么要与 $\left\{ \infty \right\}$ （这是个集合？）取并集？难道拓展复平面C中没有无穷远处吗？）

## 理解

我们最熟悉的应该就是

$y=Px$

这种把向量 $x$ 通过矩阵 $P \in \mathbb{R}^{n_x \times n_x}$ 变化为向量 $y$ 的函数变换。这种变换一般在一个空间里进行，比如把向量 $x$ 经过平移，放缩，旋转变成向量 $y$ 。

而从宏观角度看，线性分式变换是从一个空间里的某个位置区域变换到另一个空间里的某个位置区域。从微观角度看，初始空间里的某个位置区域内有不计其数的向量 $x$ ，对其中的每个向量 $x$ 进行 $y=T(x)$ 变换，得到了不计其数的变量 $y$ ，组成了变换后空间内的某个位置区域。（我个人感觉，这就好比原来我们一次搬一个箱子，现在我们一次搬一车箱子。如果用图画出来的话就是

与

其中的坐标系为包含原始空间（向量）和变换后空间（向量）的更高维度空间所设。）比如这种旋转加放大的线性分式变换：

（可以看到左图表示原始空间，坐标轴为 $x, y$ ；右图表示变换后的空间，坐标轴为 $u, v$ ，也就是前文所谓的扩展复平面 $C$ 。这两个空间都是复平面。）

又比如在上述基础上再加上平移的线性分式变换：

还比如这种天翻地覆的线性分式变换：

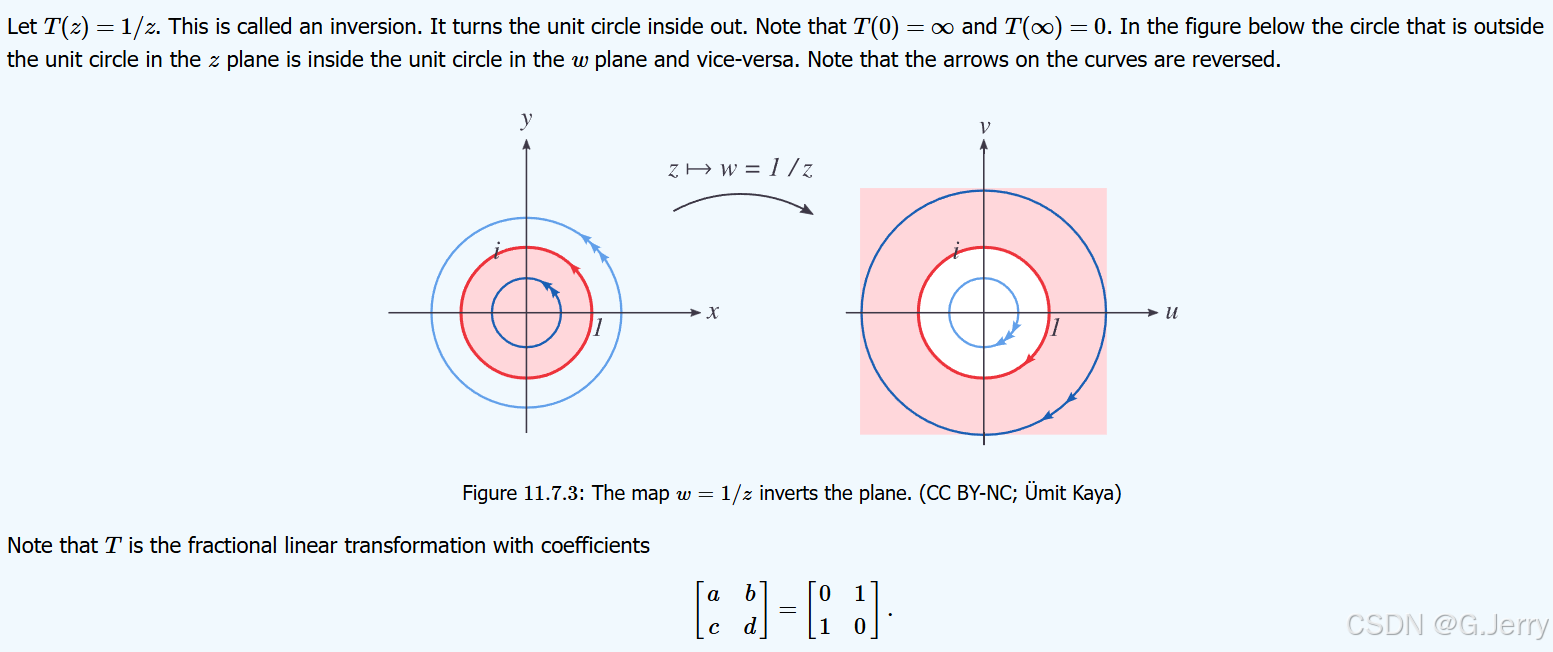
（这里把原始空间的单位圆内区域经过线性分式变换到了变换后的空间的单位圆外。相应地，

在原始空间里，浅蓝色的线在单位圆外，但是，在变换后的空间里，它被变换到了单位圆内。

在原始空间里，浅蓝色的线在单位圆外，但是，在变换后的空间里，它被变换到了单位圆内。）

再比如这个把 “原空间的包含 $x$ 轴的上半平面区域” 经过线性分式变换到 “变换后的空间的单位圆区域” 的变换：

（从这个例子中可以看出，原始空间中无限大的区域经过线性分式变换成变换后空间中的一个有限的区域。这是一种有前途的问题转化思路：与其处理无限大的区域，不如处理它经过线性变换后的一个有限的小区域。我个人以为之所以与 $\left\{ \infty \right\}$ 取交集就是要考虑变换后空间的单位圆边界，也就是原始空间种无穷远处的情况。）