luogu P4296 [AHOI2007] 密码箱 [数论] [推柿子]

P4296 [AHOI2007] 密码箱 link

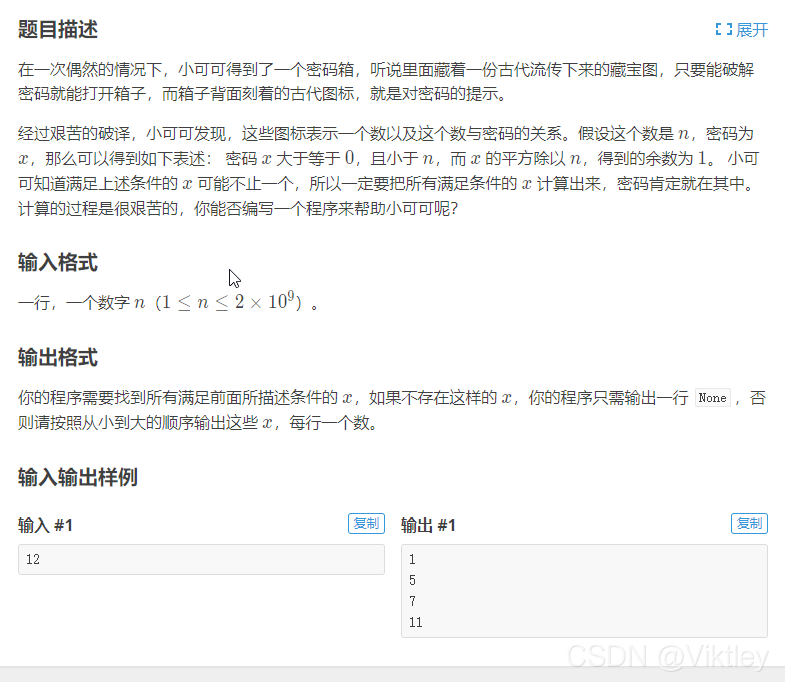
题目大意：

给定 $n$，求出所有正整数 $x$，满足小于 $n$，

且 $x^2\equiv 1\left(modn\right)$ 将满足的 $x$ 按从小到大的顺序依次换行输出

---

思路：

$x^2=kn+1$

移项发现是个平方差

即$(x+1)(x-1)=kn$

考 虑 拆 解 $k,n$

①$(x+1)=k_1\ast n_1$

②$(x-1)=k_2\ast n_2$

③$k_1\ast k_2=k,n_1\ast n_2=n$

发现可以枚举 $n$ 的约数 $y$，

记作其中的 $n_1$，

则有 $n_2=n/y$,$(x+1)=k1\ast y$④

因为 $x<n$,$x+1<=n$，考虑枚举倍数$k_1$，

假设当前枚举倍数为 $d$

则有 $(x+1)=d\ast y$

即 $x=d\ast y-1$⑤

④⑤带入②，则有 $(d\ast y-2)=k_2\ast (n/y)$

若 $(d\ast y-2)$ 为 $(n/y)$ 的倍数，则 $x=d\ast y-1$ 为一组符合的解

同理可以将 $y$ 记作其中的$n_2$，即由②推①

则有 $(d\ast y+2)=k1\ast (n/y)$

若 $(d\ast y+2)$ 为 $(n/y)$ 的倍数，则 $x=d\ast y+1$ 为一组可能的解，

因为这里是 $(x-1)->(x+1)$，$x$ 可能大于 $n$

ps:

1. 一组约数 $y$ , $n/y$，可能对应两个解
   即 $y->x-1,(n/y)->x+1$ 或者 $y->x+1,(n/y)->x-1$
2. 枚举倍数时，选择大于 $\sqrt{n}$ 的，
   不然 $\sum (k_i)$ 可能和会很大
   然后对于每个枚举的 约数，
   可以 $(x-1)->(x+1)$ 或者 $(x+1)->(x-1)$

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;
ll n, ans[N], num, cnt; 
  
void Jud(ll y) 
{
	for (ll d = 0; d <= n / y; d++) 
	{
		num = (d * y - 2);
		if (!(num % (n / y))) ans[++cnt] = d * y - 1;		
		num = (d * y + 2);
		if (!(num % (n / y))) ans[++cnt] = d * y + 1;
	}
}

int main() {
	scanf("%lld", &n);
	if (n == 1) { printf("None\n"); return 0; }
	ll siz = sqrt(n);
	for(ll i = 1; i <= siz; i++) if (!(n % i)) Jud(n / i);
	sort(ans + 1, ans + cnt + 1);
	int m = unique(ans + 1, ans + cnt + 1) - ans - 1;
	int l = 1, r = m;
	while (ans[r] >= n) r--;
	while (ans[l] < 0) l++; 
	if (!(r - l + 1)) printf("None");
	else for(int i = l; i <= r; i++) printf("%lld\n", ans[i]);
}