机器学习六(决策树ID3算法原理和实现——西瓜书学习笔记)

1.前言

西瓜书决策树学习笔记，了解决策树原理（具体理解请参看西瓜书决策树章节），手动实现决策树的西瓜分类，数据来自西瓜书给的例子。

2.决策树算法流程（伪代码——西瓜书贴图）

说明：算法代码完全按照该流程编写，结果有些不同，但感觉还挺对的。

3.实验数据

说明：来自书上数据，手敲了一下。最后一列自己加的，用于跟踪代码。属性名称单独给出，对应数据0，1，2，3，4，5列。
属性：

'色泽', '根蒂', '敲声', '纹理', '脐部', '触感'

样本数据（需要使用，请复制黏贴到txt中，python代码修改txt路径）：

青绿,蜷缩,浊响,清晰,凹陷,硬滑,是,1
乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,是,2
乌黑,蜷缩,浊响,清晰,凹陷,硬滑,是,3
青绿,蜷缩,沉闷,清晰,凹陷,硬滑,是,4
浅白,蜷缩,浊响,清晰,凹陷,硬滑,是,5
青绿,稍蜷,浊响,清晰,稍凹,软粘,是,6
乌黑,稍蜷,浊响,稍糊,稍凹,软粘,是,7
乌黑,稍蜷,浊响,清晰,稍凹,硬滑,是,8
乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,否,9
青绿,硬挺,清脆,清晰,平坦,软粘,否,10
浅白,硬挺,清脆,模糊,平坦,硬滑,否,11
浅白,蜷缩,浊响,模糊,平坦,软粘,否,12
青绿,稍蜷,浊响,稍糊,凹陷,硬滑,否,13
浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,否,14
乌黑,稍蜷,浊响,清晰,稍凹,软粘,否,15
浅白,蜷缩,浊响,模糊,平坦,硬滑,否,16
青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,否,17

4. python代码

# 手动实现决策树ID3算法

import numpy as np
import math
import pandas as pd

class Node:
    # 属性
    a_i = None
    # 属性值
    a_value = None
    # 孩子节点
    child_list = []
    # 分类
    class_y = None
    # 输出显示（a_i+a_value）
    print_content = None
    # 增益
    best_gain = None

class DecisionTree:
    root = None
    labels = []
    # 属性对应样本值集合
    attr_value_set = {}

    def __init__(self, data, labels):
        self.root = Node()
        self.labels = labels
        for label in self.labels:
            col_num = labels.index(label)
            col = [a[col_num] for a in data]
            self.attr_value_set[label] = set(col)

    # 计算类别的熵
    # param: 数据集（格式：[[绿色，硬皮，好]]）
    # 最后一列是分类
    def calculate_entropy(self, data):
        # 数据量
        row_num, col_num = np.shape(data)
        # 各个类别的数量(类别名：数量)
        label_count = {}
        for row in data:
            current_label = row[-2]
            if current_label not in label_count.keys():
                label_count[current_label] = 0
            label_count[current_label] += 1
        entropy = 0
        # 计算类别的熵
        for key in label_count:
            prob = float(label_count[key]/row_num)
            entropy -= prob*math.log2(prob)
        return entropy

    # 找得类别中最多的
    def majority_class(self, class_y):
        y_count = {}
        for y in class_y:
            if y not in y_count.keys():
                y_count[y] = 0
            y_count[y] += 1
        max_count = 0
        max_key = class_y[0]
        for key in y_count:
            if y_count[key] > max_count:
                max_count = y_count[key]
                max_key = key
        return max_key

    # 划分数据集，根据属性ai,获取值为ai_v的数据集data_v
    # i：第i个属性（这里data第i列）
    # v: ai第v个取值
    def split_data_v(self, data, i, v):
        data_v = []
        for row in data:
            if row[i] == v:
                reduced_row = row[:i]
                reduced_row.extend(row[i + 1:])
                data_v.append(reduced_row)
        return data_v

    # 最优划分属性，根据熵，增益,返回属性列序号
    # best_attr: 属性值，data列序号
    # best_gain: 最大属性增益
    def find_best_attr(self, data):
        # 属性的数量
        attr_num = len(data[0]) - 1
        # 计算D的熵
        ent_d = self.calculate_entropy(data)
        # 增益
        best_gain = 0
        # 最优属性序号(0~len(data)-1)
        best_attr = -1
        for i in range(attr_num):
            # 属性ai所有取值，data第i列
            attr_i = [a[i] for a in data]
            # 属性ai所有取值
            attr_iv_set = set(attr_i)

            # 属性ai的v个取值的熵求和(例：ai表示色泽，ai_v=青绿，v=0,1,2...)
            # sum: |D^v|/|D|*ent(D^v)(v=0,1,2...)
            sum_ent_dv = 0
            for attr_iv in attr_iv_set:
                data_v = self.split_data_v(data, i, attr_iv)
                prob = len(data_v)/len(data)
                sum_ent_dv += prob*self.calculate_entropy(data_v)
            gain_v = ent_d - sum_ent_dv
            # 获取最大增益和对应属性
            if gain_v > best_gain:
                best_gain = gain_v
                best_attr = i
        return [best_attr, best_gain]

    def create_tree(self, data, labels, node=None):
        # 初始化根节点
        if node is None:
            node = self.root
        # 获取分类列(data最后一列)
        class_y = [cls[-2] for cls in data]
        # 分类相同，标记为叶子节点
        if class_y.count(class_y[0]) == len(class_y):
            node.class_y = class_y[0]
            return
        # 属性为空，或者data中样本在属性上取值相同，类别标记为data中最多的一个
        # data[0] == 1说明，只有最后一列类别，属性已经全部剔除
        # if len(data[0]) <= 2:
        if labels is None or len(labels) == 0:
            node.class_y = self.majority_class(class_y)
            return
        # 从属性中找到最优划分属性(ID3算法)
        best_attr, best_gain = self.find_best_attr(data)
        node.a_i = labels[best_attr]
        node.best_gain = best_gain
        # 最优属性ai所有样本值，data第i列
        # attr_i = [a[best_attr] for a in data]
        # 最优属性ai所有取值
        attr_iv_set = self.attr_value_set[node.a_i]
        for attr_iv in attr_iv_set:
            # 为node生成一个分支节点，data_v表示data在属性attr_i取值为attr_iv的样本集合
            child_node = Node()
            child_node.child_list = []
            # 父节点属性+值
            child_node.print_content = node.a_i+attr_iv
            child_node.a_value = attr_iv
            node.child_list.append(child_node)
            data_v = self.split_data_v(data, best_attr, attr_iv)
            # data_v是空，标记为叶子节点，分类属于data中节点最多的
            if data_v is None or len(data_v) == 0:
                class_v_y = [cls[-2] for cls in data]
                child_node.class_y = self.majority_class(class_v_y)
            else:
                # 去掉最优属性
                label_v = labels[:best_attr] + labels[best_attr + 1:]
                self.create_tree(data_v, label_v, child_node)
        return

    # 给定属性，进行预测，树前序遍历
    def predict(self, x, node=None):
        if node is None:
            node = self.root
        if node.class_y is not None:
            print(node.class_y)
            return node
        # 节点对应属性位置
        ai_index = self.labels.index(node.a_i)
        ai_v = x[ai_index]
        print(node.a_i)
        if len(node.child_list) > 0:
            for child_node in node.child_list:
                leaf = None
                if child_node.a_value == ai_v:
                    print(child_node.print_content)
                    leaf = self.predict(x, child_node)
                if leaf is not None:
                    return leaf


    # 层序遍历树
    def bfs_tree(self):
        queue = []
        if self.root is not None:
            queue.append(self.root)
        while queue is not None and len(queue) > 0:
            # 每层节点数
            level_num = len(queue)
            for i in range(level_num):
                if len(queue[0].child_list) > 0:
                    for node in queue[0].child_list:
                        queue.append(node)
                print_content = queue[0].print_content if queue[0].print_content is not None else ""
                if queue[0].a_i is not None:
                    print(print_content, queue[0].a_i, queue[0].best_gain, end=' ')
                    print(",", end=' ')
                if queue[0].class_y is not None:
                    print(print_content, queue[0].class_y, end=' ')
                    print(",", end=' ')
                del queue[0]
            print(" ")


def create_data_set():    # 创造示例数据
    data_set = pd.read_table('data/watermelon_data.txt', header=None, encoding='utf8', delimiter=',')
    data_set = np.array(data_set).tolist()
    labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']  #两个特征
    return data_set, labels


dataSet, label = create_data_set()  # 创造示列数据
tree = DecisionTree(dataSet, label)
tree.create_tree(dataSet, label)  # 输出决策树模型结果
tree.bfs_tree()
node = tree.predict(x=['浅白', '蜷缩', '浊响', '稍糊', '平坦', '软粘'])

5.实验结果

（1）层序遍历决策树结果：

纹理 0.381 ,  
纹理稍糊 触感 0.722 , 纹理模糊 否 , 纹理清晰 根蒂 0.458,  
触感硬滑 否 , 触感软粘 是 , 根蒂稍蜷 色泽 0.252 , 根蒂硬挺 否 , 根蒂蜷缩 是 ,  
色泽青绿 是 , 色泽浅白 是 , 色泽乌黑 触感 1.0 ,  
触感硬滑 是 , 触感软粘 否 ,  

格式说明：每行是树的每层
i) 根节点：(属性 增益值），如（纹理 0.381）
ii) 中间节点：(父节点属性和值 增益最大属性 增益值)，如（纹理稍糊 触感 0.722）
iii) 叶子节点：（父节点属性和值 分类），如（触感硬滑 是）

word画一下决策树图：

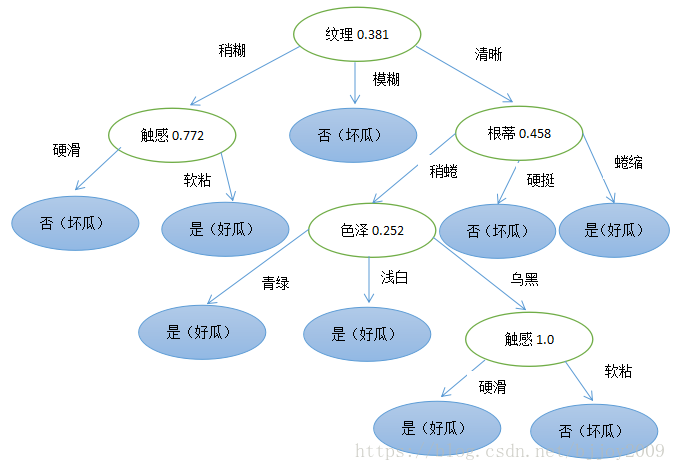
（2）给出样例在决策树汇总查找路径(x=[‘浅白’, ‘蜷缩’, ‘浊响’, ‘稍糊’, ‘平坦’, ‘软粘’])

纹理
纹理稍糊
触感
触感软粘
是

根据决策树，选择增益最大属性纹理->选择纹理属性值稍糊->增益最大属性触感->选择触感属性值软粘->结果是（好瓜）

6.总结

（1）plot画决策树略难
（2）树不能保存，没办法像sklearn一样保存训练结果持续使用
（3）实现细节挺多
（4）python，numpy，pandas数据格式需要互相转化