算法专题七：分治-CSDN博客

快排

1.颜色分类

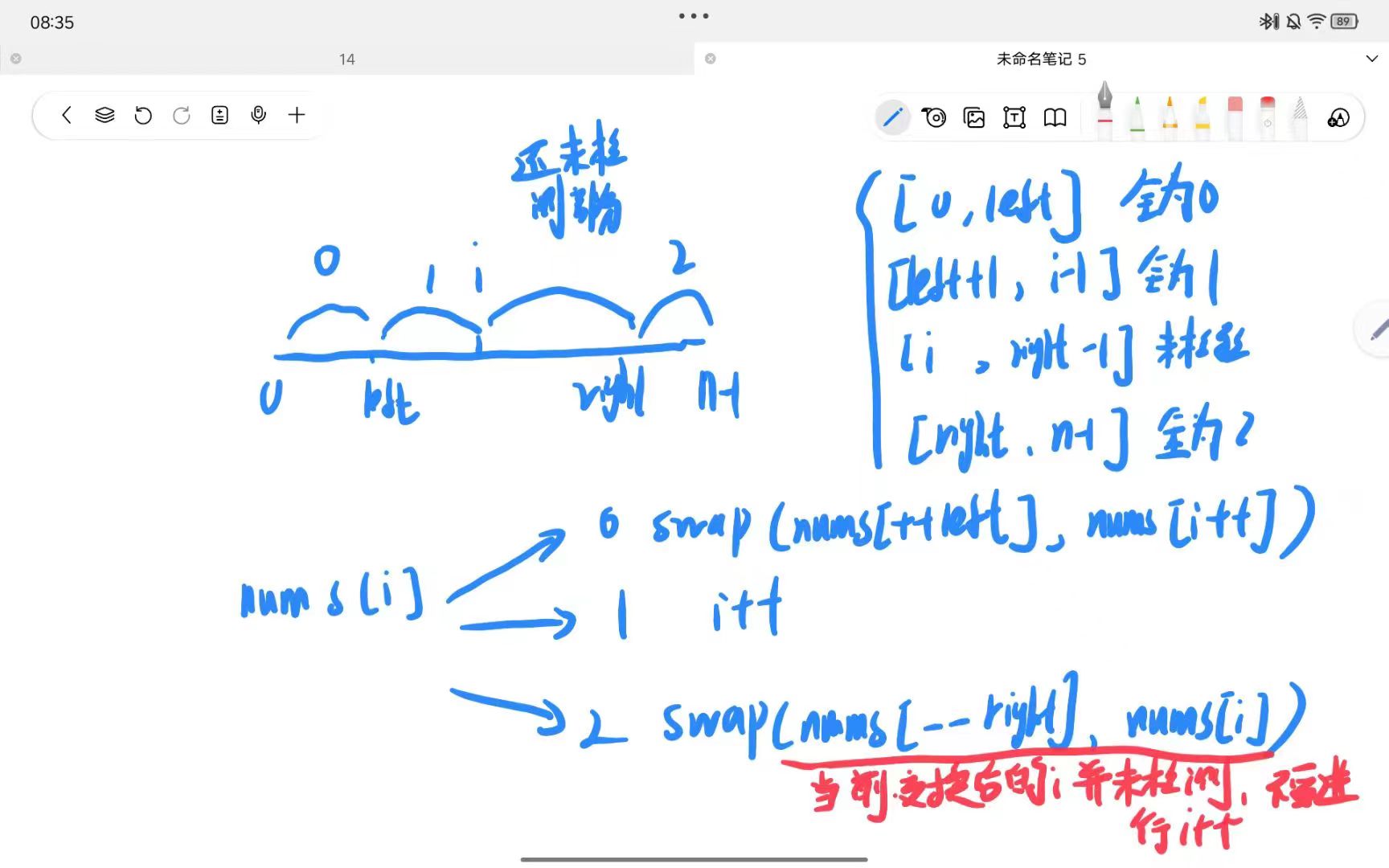
class Solution {


    public void swap(int[] nums, int i, int j){
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
    public void sortColors(int[] nums) {
        int left=-1 ,i=0 ,right=nums.length;
        while(i<right){
            if(nums[i] == 0) swap(nums, ++left, i++);
            else if(nums[i] == 1) i++;
            else swap(nums, --right, i);
        }

    }
}

2.排序数组

题目链接：912. 排序数组 - 力扣（LeetCode）

排序的规则和颜色分类的思想基本一致

那么key的值如何选择

class Solution {
    public int[] sortArray(int[] nums) {
        int left=0;
        int right=nums.length-1;
        qsort(nums,left,right);
        return nums;
    }
    public void qsort(int[] nums,int l,int r){
        if(l>=r){
            return;
        }
        int key=nums[new Random().nextInt(r-l+1)+l];
        int left=l-1;
        int right=r+1;
        int i=l;
        while(i<right){
            if(nums[i]<key){
                swap(nums,++left,i++);
            }else if(nums[i]==key){
                i++;
            }else{
                swap(nums,--right,i);
            }
        }
        qsort(nums,l,left);
        qsort(nums,right,r);
    }
    public void swap(int[] nums,int m,int n){
        int t=nums[m];
        nums[m]=nums[n];
        nums[n]=t;
    }
}

3.数组中第k个最大元素

题目链接：215. 数组中的第K个最大元素 - 力扣（LeetCode）

class Solution {
    public int findKthLargest(int[] nums, int k) {
        return qsort(nums,0,nums.length-1,k);
    }

    public int qsort(int[] nums,int l,int r,int k){
        if(l==r){
            return nums[l];
        }
        int key=nums[new Random().nextInt(r-l+1)+l];
        
        int left=l-1,right=r+1,i=l;
        while(i<right){
            if(nums[i]<key){
                swap(nums,++left,i++);
            }else if(nums[i]==key){
                i++;
            }else{
                swap(nums,--right,i);
            }
        }
        int b=right-left-1;
        int c=r-right+1;
        if(c>=k){
            return qsort(nums,right,r,k);
        }else if(b+c>=k){
            return key;
        }else{
            return qsort(nums,l,left,k-b-c);
        }
    }

    public void swap(int[] nums,int m,int n){
        int t=nums[m];
        nums[m]=nums[n];
        nums[n]=t;
    }
}

4.最小的k个数

题目链接：LCR 159. 库存管理 III - 力扣（LeetCode）

class Solution {
    public int[] inventoryManagement(int[] nums, int k) {
        qsort(nums,0,nums.length-1,k);
        int[] ret=new int[k];
        for(int i=0;i<k;i++){
            ret[i]=nums[i];
        }
        return ret;
    }

    public void qsort(int[] nums,int l,int r,int k){
        if(l>=r){
            return ;
        }
        int key=nums[new Random().nextInt(r-l+1)+l];
        
        int left=l-1,right=r+1,i=l;
        while(i<right){
            if(nums[i]<key){
                swap(nums,++left,i++);
            }else if(nums[i]==key){
                i++;
            }else{
                swap(nums,--right,i);
            }
        }
        int b=right-left-1;
        int a=left-l+1;
        if(a>=k){
            qsort(nums,l,left,k);
        }else if(b+a>=k){
            return;
        }else{
            qsort(nums,right,r,k-a-b);
        }
    }

    public void swap(int[] nums,int m,int n){
        int t=nums[m];
        nums[m]=nums[n];
        nums[n]=t;
    }
}

归并

1.排序数组

题目链接：912. 排序数组 - 力扣（LeetCode）

首先将其差分成最小的单个数字，进行排序，然后将其合并，将两个合并的时候，有可能其中一个排序完了，但另一个没有完，导致合并的循环结束，所以我们需要将未处理的数字添加到数组中，最后将数组还原成题目中给的数组

class Solution {
    int[] ret;
    public int[] sortArray(int[] nums) {
        ret=new int[nums.length];
        mergSort(nums,0,nums.length-1);
        return nums;
    }

    public void mergSort(int[] nums,int left,int right){
        if(left>=right){
            return;
        }
        int mid=(right+left)/2;

        // 排序
        mergSort(nums,left,mid);
        mergSort(nums,mid+1,right);

        // 合并
        int cur1=left;
        int cur2=mid+1;
        int i=0;
        while(cur1<=mid && cur2<=right){
            ret[i++]=nums[cur1]<=nums[cur2]?nums[cur1++]:nums[cur2++];
        }
        // 处理剩下未处理的
        while(cur1<=mid){
            ret[i++]=nums[cur1++];
        }
        while(cur2<=right){
            ret[i++]=nums[cur2++];
        }

        // 还原
        for(int k=left;k<=right;k++){
            nums[k]=ret[k-left];
        }
    }
}

2.数组中的逆序对

题目链接：LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

升序情况

class Solution {
    int[] ret;
    public int reversePairs(int[] nums) {
        ret=new int[nums.length];
        return mergeSort(nums,0,nums.length-1);
        
    }
    public int mergeSort(int[] nums,int left,int right){
        if(left>=right){
            return 0;
        }
        int mid=(right+left)/2;
        int result=0;
        // [left,mid][mid+1,right]  
        // 左半的个数+排序，右半的个数+排序
        result+=mergeSort(nums,left,mid);
        result+=mergeSort(nums,mid+1,right);

        int cur1=left;
        int cur2=mid+1;
        int i=0;
        while(cur1<=mid && cur2<=right){
            if(nums[cur1]<=nums[cur2]){
                ret[i++]=nums[cur1++];
            }else{
                ret[i++]=nums[cur2++];
                result+=mid-cur1+1;
            }
        }

        while(cur1<=mid){
            ret[i++]=nums[cur1++];
        }
        while(cur2<=right){
            ret[i++]=nums[cur2++];
        }

        for(int j=left;j<=right;j++){
            nums[j]=ret[j-left];
        }
        return result;
    }
}

3.计算右侧小于当前元素的个数

题目链接：315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

class Solution {
    int[] ret;
    int[] index;
    int[] temIndex;
    int[] temNums;
    public List<Integer> countSmaller(int[] nums) {
        int n=nums.length;
        ret=new int[n];
        index=new int[n];
        temIndex=new int[n];
        temNums=new int[n];
        for(int i=0;i<n-1;i++){
            index[i]=i;
        }
        mergeSort(nums,0,n-1);
        List<Integer> result=new ArrayList<Integer>();
        for(int x:ret){
            result.add(x);
        }
        return result;
    }

    public void mergeSort(int[] nums,int left,int right){
        if(left>=right){
            return;
        }

        int mid =(right+left)/2;
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);

        int cur1=left;
        int cur2=mid+1;
        int i=0;
        while(cur1<=mid && cur2<=right){
            if(nums[cur1]<=nums[cur2]){
                temNums[i]=nums[cur2];
                temIndex[i++]=index[cur2++];
            }else{
                ret[index[cur1]]+=right-cur2+1;
                temNums[i]=nums[cur1];
                temIndex[i++]=index[cur1++];
            }
        }

        while(cur1<=mid){
            temNums[i]=nums[cur1];
            temIndex[i++]=index[cur1++];
        }
        while(cur2<=right){
            temNums[i]=nums[cur2];
            temIndex[i++]=index[cur2++];
        }
        for(int k=left;k<=right;k++){
            nums[k]=temNums[k-left];
            index[k]=temIndex[k-left];
        }
    
    }
}

4.翻转对

题目链接：493. 翻转对 - 力扣（LeetCode）

class Solution {
    int[] tem;
    public int reversePairs(int[] nums) {
        int n=nums.length;
        tem=new int[n];
        return mergeSort(nums,0,n-1);
    }

    public int mergeSort(int[] nums,int left,int right){
        if(left>=right){
            return 0;
        }
        int ret=0;
        int mid=(right+left)/2;
        ret+=mergeSort(nums,left,mid);
        ret+=mergeSort(nums,mid+1,right);

        int cur1=left;
        int cur2=mid+1;
        int i=left;
        while(cur1<=mid){
            while(cur2<=right && nums[cur2] >= nums[cur1] / 2.0){
                cur2++;
            }
            if(cur2>right){
                break;
            }
            ret+=right-cur2+1;
            cur1++;
        }

        cur1=left;
        cur2=mid+1;
        while(cur1<=mid && cur2<=right){
            if(nums[cur1]<nums[cur2]){
                tem[i++]=nums[cur2++];
            }else{
                tem[i++]=nums[cur1++];
            }
        }
     
        while(cur1<=mid){
            tem[i++]=nums[cur1++];
        }
        while(cur2<=right){
            tem[i++]=nums[cur2++];
        }

        for(int k=left;k<=right;k++){
            nums[k]=tem[k];
        }
        return ret;
    }
}