详解状压DP

题目大意：

在一个  的图中选  个点，使得以每个点为中心的九宫格内有且只有它一个点，问方案数；

分析：

最笨的方法是常规搜索：从第 1 个格子开始，判断之后的每个格子能不能放国王，放完所有k个点得到一些答案；然后又从第 2 个格子开始，......；为了避免方案重复，只考虑当前开始格子之后的格子，之前的不管，否则会重复方案。将这些答案加起来就是答案。

明显这种方法会超时。

进阶分析：

你会发现相邻格子会影响放的位置，同理相邻的行也会影响放的位置；

如果把一个格子一个格子分析变成一行一行分析不就节省时间了吗？

假设我们有一行已经放好了国五，是下图这样放的（红色位置表示放国王）：

正常操作：我们可以开一个一维数组  表示第  个位置有没有放上国王；

但是这样在判断该行哪些位置放了国五时需要遍历整个f数组，

由于每个格子只有两种状态：放国王 和 不放国王 ，所以我们可以用  表示放国王， 表示不放国王；

那么把每个格子的数连起来就是：

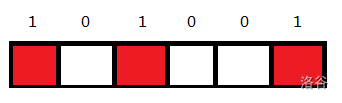
这是什么？如果我们将这个01串看成是一个二进制数的话，那么这种状态就被我们完美的表示成了一个数，这个数在十进制下是：

利用这个数就简单地表示了这一行的状态。（这就叫状态压缩）

接下来，怎么考虑下一行呢？明显是要根据当前行去推出下一行的状态，所以就有了dp动态规划的影子。

DP第一步：

按照DP的套路，我们要分析有哪些因素（变量）：

1、当前在考虑第几行（前面的行已经都放好了）？（用变量 表示）

2、当前行的状态如何？（用变量 表示）

3、到当前行为止放了几个国王？(用变量 表示）

4、至当前行为止的方案数？（这个是待求项）

那么就可以用  表示：我们已经选到了第  行，第  行的状态为 ，用了  个国王的方案数；

第二步：分析转移方程：

首先看一下国王的攻击范围（以其为中心的九宫格）：

红色代表国王位置，蓝色代表它的攻击范围：

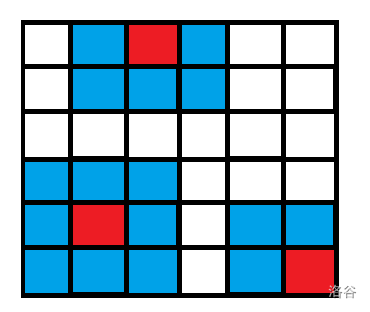
思考：如果我们第  行的第  列放好国王之后，那么对第  行的影响是什么呢？

也就是国王在第  行上的攻击范围内的格子不能再放国王了：

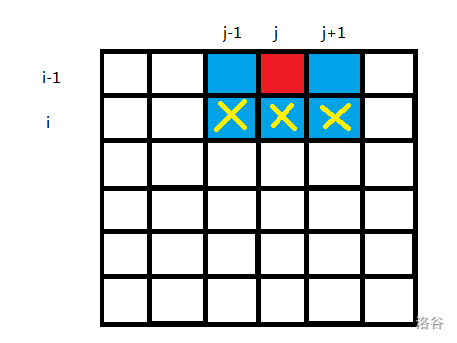
也就是说，如果第 i−1 行的状态 S1​（表示状态的二进制数）的第 j 位是 1（放国王）的话，第 i 行的状态 S2​ 的第 j−1，j，j +1 列一定为 0（不能再放国王了），否则就是不合法的状态；

那怎么表示这一条件呢？回归到二进制上来看：

假如我们现在正在决定第 i 行的状态：

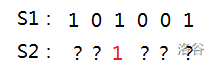
显然这个红色的 1 是不合法的，但是怎么知道它是不合法的呢？

这里就要运用巧妙的位运算了：

此时  &   ；

那如果是右下方有一个国王呢？

我们可以按照刚刚那样的方法用位运算：

1. 先将 S2​ 向左移一位：

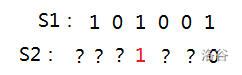
2. 然后这样两个 1 就冲齐了，此时两种状态的 & 运算是不为 0 的；

(S2​<<1) & S1​  0；

在左下方的情况同理：

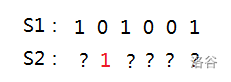
1. 我们先将 S2​ 向右移一位：

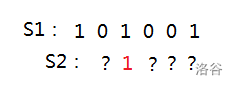
2. 然后发现此时两状态的 & 运算不为 0；

(S2​>>1) & S1​  0；

所以我们就得出了表示这三个位置的方法，那么 S2​ 必须满足什么条件才可能由 S1​ 转移过去呢？

条件：(S2​ & S1​ ==0) && ((S2​<<1) & S1​)==0) && ((S2​>>1) & S1​==0)

我们发现这样写有点长，还可以这样写哦：

(S2​∣(S2​>>1)∣(S2​<<1)) & S1​==0

当然，我们处理完行间的限制后，接下来就要处理行内的限制了；

一个国王的左右格子内不能再放国王了，这就是行内的限制！

运用上面的第二，三种情况的做法，问题就迎刃而解了：

1. 判断左边有没有国王：

我们将 S2​ 向右移一位，再与原来的 S2​ 做 & 运算：

观察到 1 左边的数右移后跑到了 1 的位置上，所以我们再做一次 & 运算即可：

若结果为 0 ，说明那一位是 0（合法）；否则为 1（不合法）；

2. 判断右边有没有国王：

同理，将 S2​ 左移一位再做 & 运算：

把上述过程转化成代码：

((S2​<<1) & S2​==0) && ((S2​>>1) & S2​==0)

更短的写法：

((S2​<<1)∣(S2​>>1)) & S2​==0

所以我们下一步的状态 S2​ 要同时满足这两个条件才可以哦~

因为第二个条件只与状态的情况有关，所以我们可以预处理这个东西，dp 的时候将所有满足第二条性质的状态拿出来看看是否再满足第一条性质就好了；

考虑第二维怎么转移的：

显然对于第 i−1 行来说，第 i 行多放的国王数就是第 i 行的状态上 1 的个数（在二进制下）；

综上，则有 dp[i][j][S2​]+=dp[i−1][j−cnt[S2​]][S1​] ，（其中 S2​ 要满足上述两个条件，cnt[S2​] 表示 S2​ 在二进制下有几个 1）

发现转移方程类似于背包 dp 时的方程

边界设置

刚开始一个偌大的棋盘，我们啥也不知道，只知道它的第 0 行不能放旗子（先说有第 0 行嘛qwq）；

即 dp[0][0][0]=1；

答案输出

最后的情况，肯定是我们已经考虑完 n 行的排放情况，并且在其中一定是只放了 k 个国王了，但对于第 n 行具体摆成什么稀奇古怪的亚子，我们也不知道，所以我们去枚举第 n 行所有可能的情况，统计答案就好了；