数列的前缀和:
sum[i]表示a[1]~a[i]的和
用处1:求i~j的和sum[j]-sum[i-1]
用处2:区间修改。设置一个change数组。当区间[i,j]上要加k时,我们令change[i]+=k,令change[j+1]-=k。如果我们对change数组求前缀和的话,前缀和sum_change[i]就是i这个位置变动的值
树的前缀和有两种
– 根路径前缀和sum2[i],指i到根节点所有节点的权值之和。
– 子树前缀和sum1[i],指i的子树(包括i本身)所有节点的权值之和。
树的前缀和用处
–根路径前缀和,可以用来求路径节点权值和(配合lca食用)
–假如要求x到y路径的权值和,x,y的lca是z。则可以用sum[x]+sum[y]-2sum[z]+value[z]
–子树前缀和,可以用来做路径修改(也得配合lca食用)
–设定一个修改数组change。如果要对x到y路径上的所有点权值+k,lca为z。那么change[x]+=k,change[y]+=k,change[z]-=k,change[fa[z]]-=k。这样如果最后对change[i]求前缀和的话,最后得到的结果就是i权值的修改量
–特点:可以O(1)修改,但是只能一次查询(因为要求前缀和O(n))
前缀和的使用不都是用来差分的?
二维数组的差分:Ans=sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]
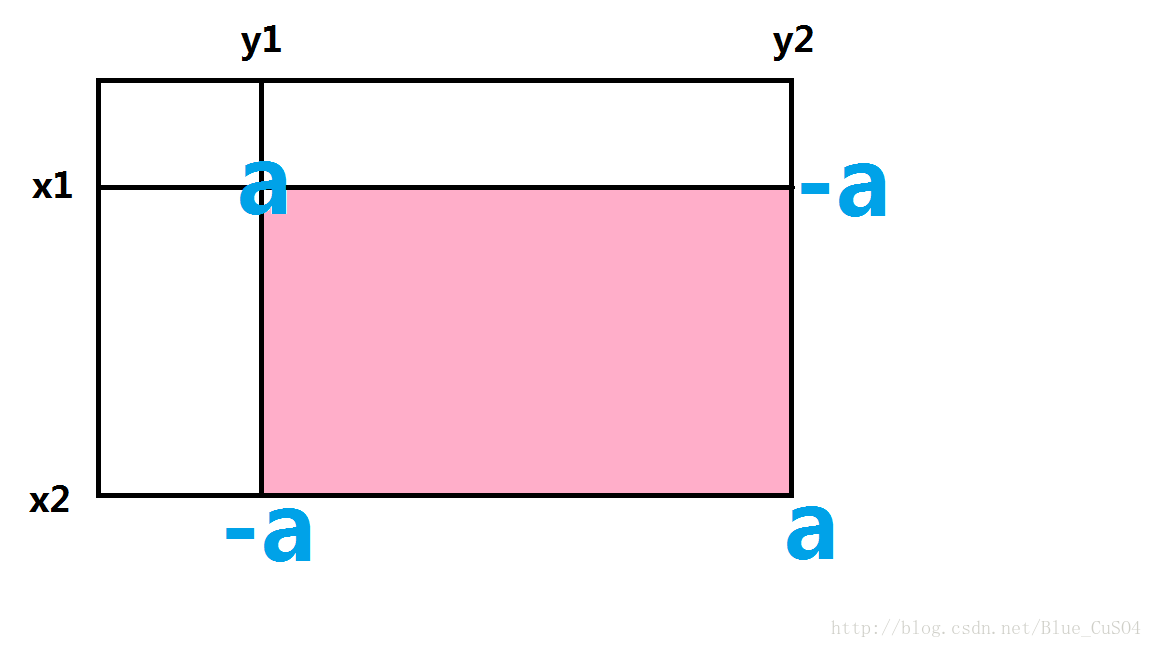
二维数组的修改:用数组C存修改信息。在C[x1][y1]处加上a,在C[x2+1][y1]和C[x1][y2+1]处减a,在C[x2+1][y2+1]再加上a。
最后(i,k)位置上变化的数值就是C数组在(i,k)位置的前缀和。
基本就是
树上差分经典思路
①利用dfs序的时间戳,一个点拆成两个点,每次在in+1,在out-1,然后bit统计前缀和,资瓷动态修改和查询子树访问次数。用于子树打标记。
②对于点x,y设r=lca(x,y)。在x+1,y+1,r-2,然后从所有叶节点往上累加。用于树链打标记,资瓷查询某条边的访问次数。
③对于点x,y设r=lca(x,y)。在x+1,y+1,r-1,father[r]-1,然后从所有叶节点往上累加。用于树链打标记,资瓷查询某个点的访问次数。





















 1606
1606











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








