iParker：智能停车系统

iParker—一种基于动态资源分配与定价的新型智能停车系统

摘要

在主要城市中，尤其是在交通密集的情况下，停车直接影响交通流量和人们的生活。本文介绍了一种基于智能资源分配、预约和定价的新型智能停车系统。该系统通过为驾驶员提供成本最低、寻找时间最短的有保障的停车预约，同时为停车场管理者实现最高收入和资源利用率，从而解决当前的停车问题。本文还提出了新的公平定价策略，可在实际中实施。该新系统基于混合整数线性规划（MILP）的数学建模，旨在最小化驾驶员的总货币成本，并最大化停车资源利用率。

关键词 —动态定价，动态资源分配，混合整数线性规划（MILP），预约，智能汽车停车。

一、引言

PARKING 在金钱或为寻找“免费停车位”所花费的时间和精力方面，都是一项昂贵的过程。目前的研究表明，一辆汽车在其生命周期中95%的时间处于停车状态，只有5%的时间在路上行驶[1]。以2014年英国的情况为例，根据英国国家旅行调查[2]，平均每辆汽车每年行驶361小时，这意味着约有8404小时汽车处于停车状态。那么，在如此长的时间里，你会把车停在哪里呢？随着全球汽车拥有者数量的增加，“寻找停车位”自然成为首要问题。平均而言，30%的交通流量是由驾驶员四处寻找停车位造成的[3]。2006年，一项法国的研究估计，法国每年有7000万小时花在寻找停车位上，导致每年经济损失达7亿欧元[4]。2011年，IBM®[5]的一项全球停车调查显示，寻找理想停车位平均需要花费20分钟。根据这些统计数据，我们可以推断，全球很大一部分污染和燃油浪费与寻找停车位有关。

一些地方的停车位非常充裕，而在其他地方则很难找到。定价策略几十年来，在整体停车可用性方面发挥了重要作用[6]。这里出现了一个重要问题：我们是否需要更多的停车位，还是需要更好的停车管理？我们认为是后者，因此本研究工作的动机在于通过公平且有利可图的定价策略实现更优的停车管理。

本文提出的工作结合了停车预约和定价模型，以解决停车问题。在停车预约方面，Mouskos et al.[7]将预约过程建模为一个资源分配问题。他们的模型基于混合整数线性规划（MILP），目标是最小化驾驶员成本。该模型提供固定定价的实时预约。Geng et al.[8]通过考虑用户成本（包括定价和步行距离）扩展了他们的工作。此外，他们还通过引入公平性约束并进行大规模仿真进一步完善了模型。尽管[8]中提出的系统表现优异，但其模型仍存在局限性，仅适用于短期预约，且未考虑停车收入。

在定价方面，舒普等[3]提出了新概念，推动了旧金山停车系统（SFPark）[9]在旧金山的建立，该系统旨在通过基于传感器历史数据动态调整价格来缓解交通拥堵。在SFPark中，传感器被部署在沥青路面上，用于收集停车信息，并将数据存储在数据库中，按周或月进行处理。根据历史数据，价格会按照预期利用率的比例进行升降调整。尽管动态变化的停车价格能够平衡停车供需关系并提高整体利用率，但其依赖于历史数据和统计结果，可能不够准确，难以达到理想效果。

本文提出了一种新的智能汽车停车系统，名为 iParker，该系统结合了静态资源调度、动态资源分配和定价模型，旨在优化停车场管理者和驾驶员双方的停车系统。本工作的贡献包括：1）提高停车资源利用率；2）增加停车收入；3）通过降低成本、减少寻找停车位时间和步行时间来改善驾驶员的停车体验。我们的工作与[8]中的研究不同，后者提出了一个动态资源分配模型。该模型的主要局限性在于：仅允许在有限时间段内（例如几分钟）进行预约，采用固定价格，未考虑收入，且只考虑单一目的地选择。而我们的模型允许驾驶员为未来任意时间预约停车位，考虑了收入因素，并引入了新的定价模型。此外，还提出了一种结合个人行程规划器的停车解决方案。我们在定价方面的研究也与舒普的研究不同，我们提出了停车领域的实时动态定价，并证明了其有效性。

本文其余部分组织如下：第二节介绍相关工作。第三节介绍所提出系统的概述、架构与响应机制。第四节描述并构建了智能资源分配模型。第五节展示了大规模仿真与讨论结果。最后，第六节对本文进行总结。

II. 相关工作

在过去二十年中，汽车停车领域已开展了大量研究并投入了大量资金。其中一些研究已应用于实践，例如停车引导与信息系统（PGI系统）[10]–[12]。PGI系统通过可变信息标志向驾驶员提供受控区域内停车场的实时信息。它们主要利用部署在停车场出入口的传感器来收集总占用率信息。其他实现方式通常在每个停车位配备一个传感器，这种做法已在商业购物中心和商业区中出现，以进一步提高停车位利用率并减少寻找时间。

大多数研究都集中在如何检测停车位的占用状态[13]–[16]。然而，这些系统仍未解决所有问题。停车监控区域内的停车资源竞争导致交通拥堵加剧，同时其他停车资源却处于空闲状态。这也引发了“多辆车争抢同一车位”的已知现象。尽管掌握停车区域的占用状态数据确实至关重要，但更重要的是高效利用这些数据。

还有其他研究人员探讨了停车预约系统。例如，Trusiewicz et al.[17]采用非结构化补充服务数据（USSD）作为驾驶员与停车预约系统之间的通信媒介。尽管大多数网络运营商使用USSD并非免费，但它仍是一种用于停车预约的廉价且可靠的技术。Inaba et al.[18]利用RFID标签存储和更新预约状态，并讨论了实时预约与共享时段预约之间的区别，两者的差异在于：在共享时段预约中，由于资源时间是共享的，驾驶员必须在已知的进出时间窗口内使用服务；而在实时预约中，驾驶员可以不受其他驾驶员影响，以无限的时间间隔进行停车。Wang et al.[19]提出了一种分布式系统的原型，该系统包含一个中央处理器，用于收集预约请求并将其重定向到相应的本地处理器。他们的系统利用蓝牙和Wi‐Fi来检测停车场内的占用状态，并相应地通知驾驶员可用停车位。

短消息服务（SMS）预约在许多研究论文中被提出。例如，Hanif et al.[20]开发了一种使用微控制器、键盘、门禁控制和远程终端单元（微型RTU）的嵌入式短信预约系统。微型RTU是一种带有处理器和GSM模块的独立终端，用于接收短信并触发I/O引脚。互联网预约已在[21]通过使用ZigBee和压力传感器的传感器网络来检测停车位的占用状态。驾驶员可通过网站进行预约。这些预订系统确实能够减少整体停车问题。然而，它们主要关注驾驶员与系统之间的通信技术或媒介，很少涉及能够以高效管理预约并带来显著改进的模型或算法。

桥本等人提出了一种基于拍卖的预约系统，在该系统中，预约过程有一个间隔时间，驾驶员需要在截止时间前注册，系统将根据最高出价分配停车位。总体而言，基于拍卖的方法可能导致许多公平性问题。

III. iParker—系统概述

我们的新理念是将实时预订（RTR）与共享时间预订（STR）相结合，从而使驾驶员可以在前往目的地途中（例如几分钟内到达）预订停车位，也可以提前任意时间（例如几天前）进行预订。RTR通过执行动态资源分配来实现，类似于呼叫中心中的基于技能的路由。在RTR情况下，系统会持续为驾驶员分配到达目的地前可用的最佳停车位。而STR则通过基于时间调度的静态资源分配实现，驾驶员可明确选择首选资源及其在未来任意时间的占用时间范围。本文提出了针对这两种预订类型的公平定价策略，兼顾驾驶员和停车场管理者的利益。此外，还引入了一个动态定价引擎，该引擎根据占用率、预约情况及其他事件所反映的实时资源利用率，定期更新停车价格。iParker 支持普通和残疾人停车位，并允许驾驶员自由选择多个目的地，系统将根据其选定的目的地和具体情况分配最优资源。

在本文中，我们将使用术语“parker”指代驾驶员或汽车，“资源”指代一组停车位，“D型”指代动态预订、RTR或请求动态预订的驾驶员类型，“S型”指代静态预订、STR或请求静态预订的驾驶员类型。

A. 架构与响应方案

iParker 是一个半分布式系统，如图1所示：系统包含一个中央请求中心（CRC）、一个停车场管理员（PM）和多个本地智能分配系统（SAS）。

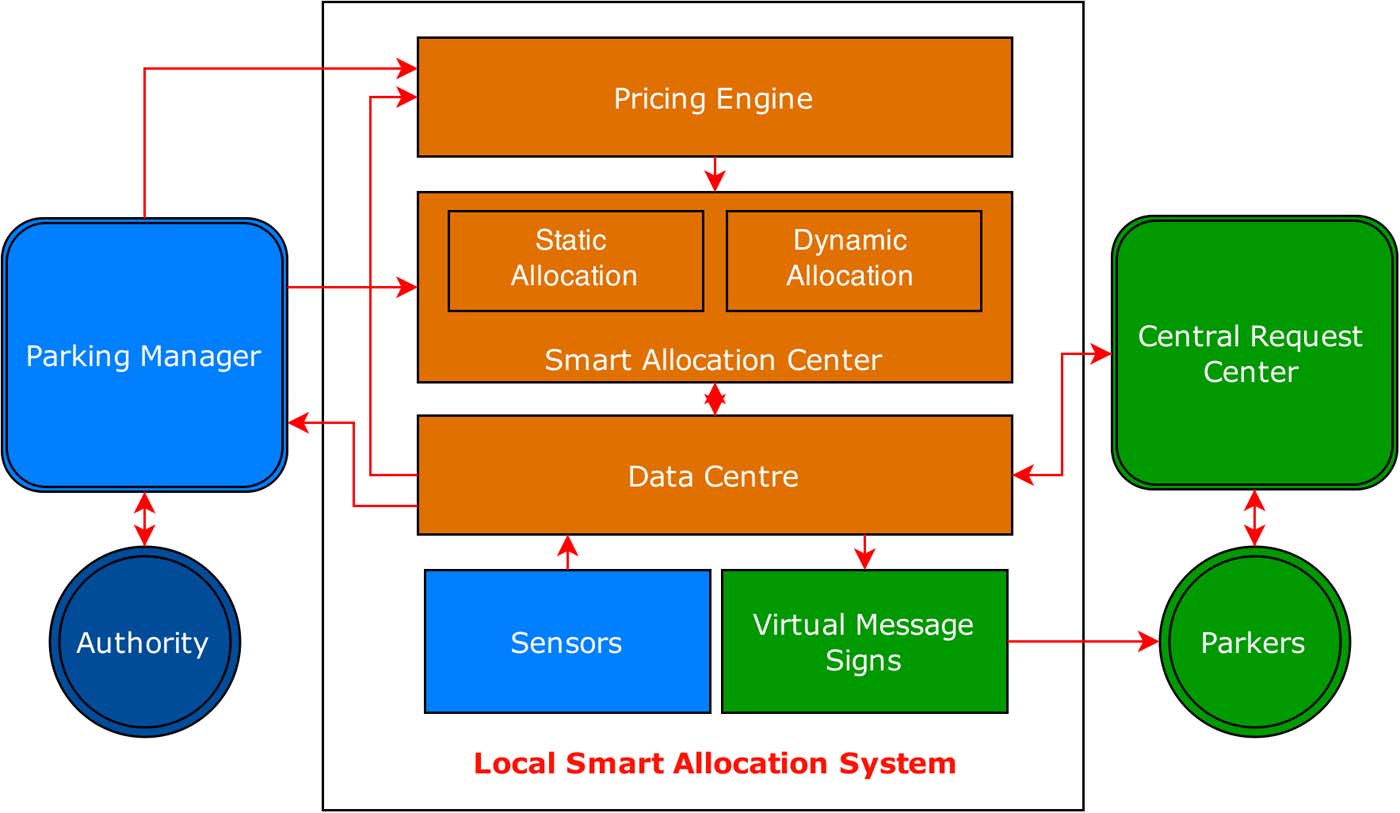
中央预留控制器（CRC）接收停车者的请求，处理并将其转移至相关的本地智能分配系统（SAS）。请求过程如下：停车人选择一个或多个目的地，如果其为S型，则可选择首选停车资源。两种类型均需分配一个0到1之间的权重参数，以反映其对资源与目的地的接近程度和资源价格之间的偏好程度。两种类型还需设定可接受的最高价格和最大步行距离。对于S型，必须定义占用间隔。对于D型，会测量GPS坐标并将其附加到请求中。最后，将停车者身份信息（即驾驶员和车牌号码）随请求一起发送。中央预留控制器（CRC）还会向所有停车者回复预约报价，并以相同方式通知本地智能分配系统（SAS）停车者的响应。

中央停车管理者（PM）是停车管理部门、停车资源管理者、智能分配系统（SAS）和本地定价引擎之间的接口。停车管理部门可以通过PM手动更新相关的定价引擎或数据中心。例如，为特定停车资源设定定价数值，或向数据中心更新相关资源附近即将发生的事件信息。

下面我们介绍本地智能分配系统的主要组件：

• 定价引擎 —定价引擎是运行在网络服务器上的小型应用程序。定价引擎的职责是每隔预定义时间间隔从停车管理部门获取停车使用数据和更新，并据此设置新的停车价格。该引擎在SAS上独立运行，计算新的价格并更新数据中心。
• 传感器 —每个资源都配备有车位占用检测系统。理想情况下，该系统必须能够准确提供停车资源的使用情况数据，无论是在室内还是室外部署。该检测系统通常由无线/有线传感器网络组成，可提供每个停车位的占用状态；或者 alternatively 由停车场出入口的计数传感器组成，仅能提供总使用率数值。后一种方法只能在受控环境中工作，因此我们更倾向于使用传感器网络和中央处理器，以实时更新数据中心的利用率数值。
• Data Centre —存储来自所有iParker组件的全部信息，并将其保存在结构化数据容器中。它包含一个价格表，其中含有每分钟每个资源的最新定价信息，包含利用率数据的使用情况表，以及由停车管理部门设置其他参数（如与事件相关）的管理部门参数表。数据中心还负责更新多种虚拟信息标志和公共设备的最新定价信息及停车可用性。
• 智能分配中心 —一个运行复杂混合整数线性规划（MILP）模型的网络服务，能够最优且公平地为停车者分配/预约停车资源。该分配基于若干关键变量，包括但不限于驾驶员限制条件、当前资源使用情况、最新定价信息以及事件发生。该中心为停车者提供不间断的停车预约服务，下一节将对此进行详细描述。
• 虚拟信息标志（VMS） —向停车人/公众提供最新的定价和停车可用性信息。这通过在城市各处尤其是路侧停车区域周围部署大量VMS显示屏来实现。对于路外停车场，在入口处设置一个VMS显示屏就足以向到达者提供更新的信息。需要特别说明的是，停车者将仅根据预约报价中确定的费率支付费用。如果停车者未使用该服务，则需根据其停车时显示的费率支付。VMS对非智能手机用户尤为重要。

IV. 智能资源分配

本研究解决的问题结合了实时预约和共享时间预约系统。实时预约通常与停车人对停车位的使用时长无关，即停车人可以根据需要使用任意时长，而不会影响其他停车者。另一方面，共享时间预约则依赖于具体的车位占用率和车位离开时间。共享时间预约通常被建模为生灭随机过程。在我们的模型中，动态预约属于实时预约，而静态预约属于共享时间预约。

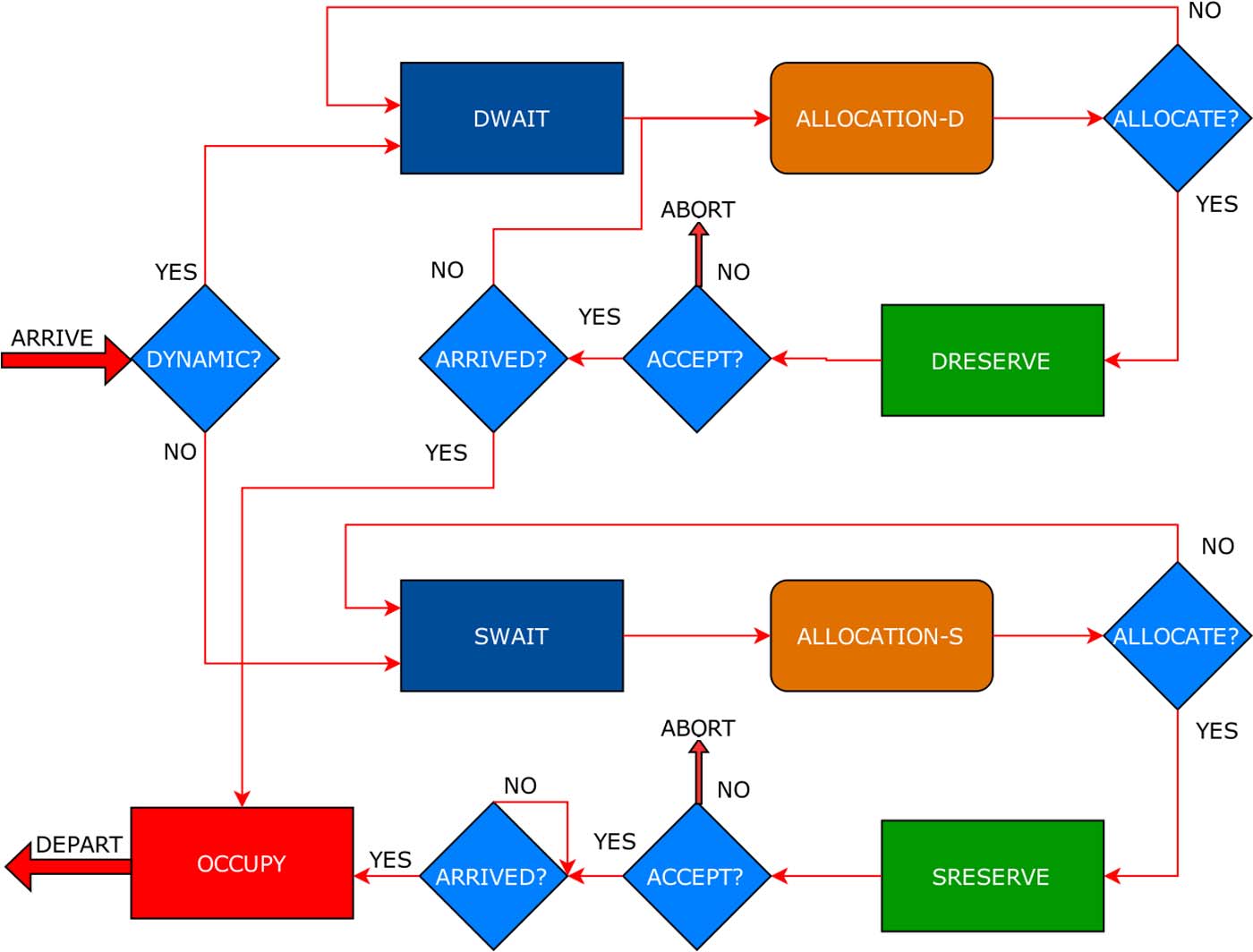
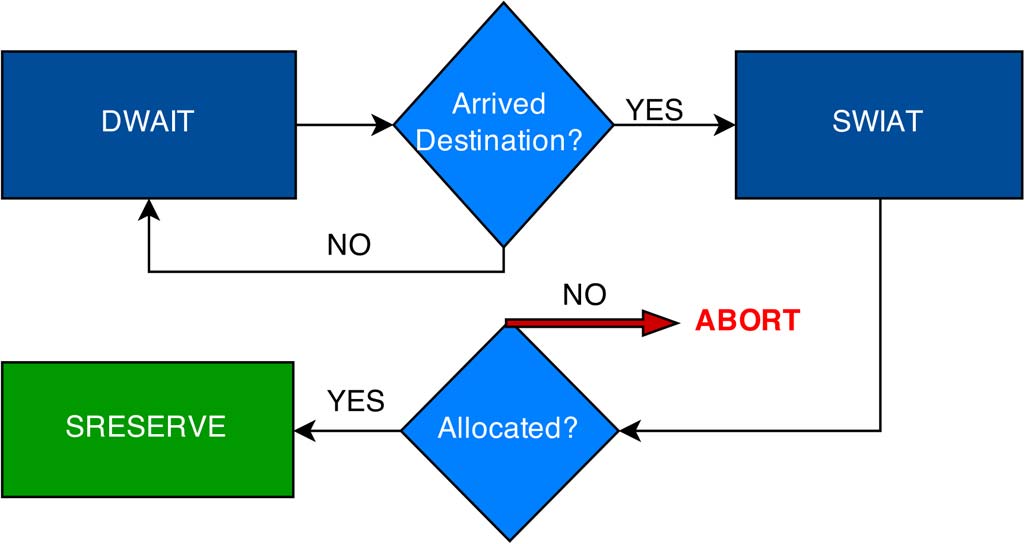
我们的混合整数线性规划（MILP）模型的目标是最小化停车者的总货币成本，并最终最大化资源利用率，以使停车场管理者获得最大收入。我们将基于图2中的排队模型来构建本模型。系统中有N个资源，其中每个资源j被划分为 P1个停车位（用于动态预约的普通停车位数量）、 P2个停车位（用于静态预约的普通停车位数量） P3以及 P4（类似于 P1和 P2，但针对残障人士）。智能分配中心的运行时间被离散化为多个小的时间段。我们将每个时间段记为一个决策点 K。所有停车者随机且独立地到达分配中心，并加入相应的等待队列（WAIT queue）。在每个决策点，分配中心将向动态停车者和静态停车者分配资源，并将其转移至相应的预留队列（RESERVE queue）。处于动态预留队列（DRESERVE）中的停车者将在每个决策点后重新分配到更优的停车位（如果可用），直到他们到达被定义为其第一个目的地的指定区域。处于静态等待队列（SWAIT）中的停车者仅会被分配一次，随后转入静态预留队列（SRESERVE）。当停车者到达其分配的资源时，他们将被移入占用队列（occupy queue），然后 P1、 P2、 P3或 P4的计数将根据停车者人数相应减少。当停车者离开停车位时，他们将从系统中完全移除，同时停车位的数量将相应增加。为了充分最大化资源利用率，我们将通过初始化系统，使50%的资源为“动态”，50%的资源为“静态”。然后我们将遵循图3中的策略：当DWAIT队列中的停车者到达其目的地时，若因 P1或 P3变为零（即动态预留者无空闲停车位）而未能成功分配，则系统会自动将其转移到SWAIT队列，使其有机会分配到“静态”资源。

A. 问题建模

在每个决策点 K，我们将如下定义智能分配系统 A(K)的状态和停车者Xi(K)的状态（定义列表见表I）：

A(K)={DW(K), SW(K), DR(K), SR(K), Z(K)}(1)
X i( K)={l i( K), ψi( K), υi( K), ωi( K), Fi( K)}. (2)

分配系统的关键输入是每个停车人有资格获得的可行资源F i( K)。为此，我们为停车者定义了一些主要属性：
1）Mi 是停车者 i能够承受的最高总价格。2） D i 是停车者 i可容忍的最大步行距离。3） ϕ i 是停车者 i所需的停车位类型。¯4）β i 是预约类型。5） P i j( K)、 P i j 和 gi(K)是描述停车资源状态的参数，将在后文解释。

下面我们定义一些关键的二元变量：

ϕi={1, if i is requesting a normal resource 0, if i is requesting a disabled resource (3)
β i ={1, if i is requesting a dynamic reservation 0, if i is requesting a static reservation (4)
υ i( K)={j, if i is reserved the resource j 0, otherwise (5)

通过定义L j 为资源 j的位置，可以按如下方式估算停车人 i 与资源 j之间在时间 K的剩余距离d i j (K)和行驶时间 τ i j(K)：

d i j(K)= ‖l i( K)− L j ‖
τ i j(K)= d i j(K)/V i( K). (6)

现在可以将停车人 i 的第一个属性 Mij(K)的定价方案设置为 τij(K)、 ψi(K)、 Ti(总占用时间) 和 Cj(K)(占用资源 j 的每小时当前价格) 的函数。如(7)所示，我们对动态停车者收取的预订费用等于其总预约时间对应的费用。另一方面，我们对静态停车者收取相当于一个占用小时价格的固定预订费用。

Mij(K)=
{
(Cj(K)/60)(ψi(K)+Ti+τij(K)), if βi=1
(Cj(K)Ti/60)+Cj(K), if βi=0.
(7)

对于静态停车者和动态停车者，我们允许他们选择多个目的地。 DLi={d1i, d2i,…,d ndi}是停车人 i所选择的目的地Di={1, 2,…, nd}的位置集合，其中 d1i为第一个目的地。每个停车人最多可选择 nd个目的地。停车人 i的第二个属性Dij(K)现在可用于表示步行总时间。公式(8)允许分配系统根据该停车人 i所选的目的地 Di，识别出离其最近的资源 j

Dij(K)=∑ n∈Di ‖dni − Lj‖. (8)

现在我们可以计算总成本函数Jij(K)，并根据权重 swi=[0 −1]对停车人 i进行最小化。如果停车人 i希望获得最便宜资源，则选择swi= 1；如果停车人 i仅关注步行距离意义上的最佳车位，则选择 swi= 0。此外，也可选择0.5的权重以平衡价格和接近度。

Jij(K)= swi Mij(K)/Mi +(1 − swi) Dij(K)/Di . (9)

备注 ：我们在本模型中采用了分组车位技术以节省计算能力，使得一个资源 j 可能拥有 N 个车位。例如，P1j = 1, P2j = 2,P3j = 3和P 1 j = 4 表示在资源 j 中，有1个普通‐动态、2个普通‐静态、3个残疾人‐动态和4个残疾人‐静态的空闲车位。

对于动态停车者，分配系统必须实时接收来自停车传感器的数据。因此我们定义Pij( K)为与停车人 i的停车类型相兼容的资源 j中的空闲动态车位数量。我们还定义gi(K)为至少包含一个空闲停车位的资源集合。gi(K)将等于空闲普通停车资源集合（表示为 σ({v10)）或空闲残疾人停车资源集合（表示为 σ¯(K)）

P i j(K)= ϕ i P1j(K)+(1 − ϕ i) P3j(K) (10)
σ(K)={j: j ∈ Resources, P1j(K)> 0}
σ¯(K)={j: j ∈ Resources, P3j(K)> 0}
gi( K)={σ(K), if ϕi = 1 σ¯(K), if ϕ = 0. (11)

Π i( K)现在可以被定义为可分配给动态停车者的可行资源集合。Π i( K)由以下方式确定

通过筛选所有资源，以匹配停车人 i在价格和接近度方面的最高界限（Mi和 Di）。如果资源 j与停车人 i所要求的类型（普通/残障）相同，且存在该类型的空闲停车位，并满足边界条件，则在决策时刻 K将 j添加到Πi中

Πi(K)={j: Mij(K) ≤ Mi, Dij(K) ≤ Di, Pij(K)> 0, j ∈ gi(K)}. (12)

我们将采用不同的方法来为静态停车者定义可行资源。正如我们之前提到的，静态预约属于共享时间预约系统。因此，分配系统将根据停车人 i占用开始时间时空闲停车位的可用情况，以及停车人的需求，向静态停车者分配资源。

我们定义 Pij为资源 j中与停车人 i的停车类型相兼容的静态车位总数，即

P¯ij= ϕiP2j+(1 − ϕi)P4j (13)

Θivj(K) 随后被计算，这是一个二元变量，当停车者 i 和 v 在同一类型资源 j 上的占用区间 SW(K) 与 SR(K) 存在冲突时，其值为1。占用间隔从 θ 开始，到 ϑ 结束。

Θivj(K)=
{
1, if((θvj ≥ θij)∧(θvj ≤ ϑij))|((θij ≥ θvj)∧(θij ≤ ϑvj)) ∧(ϕi= ϕv)∧(βi= βv)∧(i ≠ v)
0, otherwise.
}

然后我们定义矩阵 E(K) =[Θivj(K)]，并引入关键数组 conflict ij(K)，以实现对静态停车者的资源分配。

conflictij(K)= ∑ i∈SW(K),j∈Resources E(K) (14)

基于冲突ij(K)和停车人需求，可以按如下方式计算静态停车者的可行资源Φi(K)：

Φi(K)={j: Mi j(K) ≤ Mi, Di j(K) ≤ Di, conflictij(K)< P¯i j(K), j ∈ Resources}. (15)

我们将把所有停车者（动态和静态）合并到一个目标函数中。这可以通过为每种类型的停车人 i引入 F i( K)作为其可行资源集来实现。

F i( K)={Πi( K), if βi = 1 Φ K), if βi = 0. (16)

B. 目标函数

从停车人的角度来看，iParker在价格和接近度方面最小化了停车者总成本。从停车场管理者的角度来看，iParker最大化了资源利用率和总收入。我们引入二元决策变量 xij(K)，使得

xij(K)={1, if parker i is assigned resource j 0, otherwise (17)

并定义矩阵 X(K) =[xij(K)]。现在我们可以为在每个决策点 K 求解的问题建立目标函数和约束条件：

minimize ∑ i∈DW(K)∪DR(K) ∑ j∈Fi(K) xij(K) · Jij(K) + ∑ i∈DW(K)∪SW(K) (1− ∑ j∈Fi(K) xij(K)) (18)

s.t.: ∑ j∈Fi(K) xij(K) ≤ 1 ∀i ∈ DW(K)∪ SW(K) (19)
∑ i∈DW(K)∪DR(K):ϕi=1 xij(K) ≤ P1(K) ∀j ∈ σ(K) (20)
∑ i∈DW(K)∪DR(K):ϕi=0 xij(K) ≤ P3(K) ∀j ∈ σ¯(K) (21)
∑ j∈ F i( K) xij(K)= 1 ∀i ∈ DR(K) (22)
( ∑ n∈Fi( K) xin(K) ) − xmj(K) ≥ 0 ∀i, m ∈ DW(K), j ∈ Fi(K) s.t. τmj(K)> τij(K), ϕi= ϕm (23)
∑ j∈ F i( K) xij(K) · Jij(K) ≤ Jij(K−1) ∀i ∈ DR(K) (24)
xij(K) · t1ij(K)≤t0(K) ∀i∈DW(K), j ∈Fi(K). (25)

目标函数(18)可以分为两部分：∑i ∈ DW(K)∪ DR(K) ∑j∈ F i( K) xi j(K) · Ji j( K) 和 ∑i ∈ DW(K)∪ SW(K)(1−∑j∈ F i (K) xi j(K))。在本问题中，我们最小化目标函数，这将根据上述两部分产生两个效果。第一部分旨在最小化所有在 DW(K)和DR(K)中的停车者的总货币成本（见公式9），使得停车人 i将被分配其可行资源 F i中具有最低 J i j 的资源 j。请注意，此处未包含来自 SW(K)或 SR(K)的停车者，因为静态停车者仅被分配一次，且为其所选择的 j 进行分配。如果我们不在方程中加入第二部分，系统将把所有 x i j( K)设为零，从而不分配任何停车者。因此，我们引入第二部分，以尽可能多地在 DW(K)和 SW(K)中分配停车者。由于根据定义 J i j 小于1，因此在目标函数中增加一个值为1的成本足以确保资源分配最大化。

协同此问题中的约束条件可描述如下 流量：

• 容量
  1）约束条件(19)确保在DW(K)和 SW(K)中的所有停车者不能被分配超过一个资源。同时，它也表明这些停车者可能未被分配，即xij(K) = 0。
  2）约束条件(20)和(21)表示，在时间 K，将获得预约的动态停车者（位于 DW(K)中的停车者）与之前已获得预约的停车者（位于DR(K)中的停车者）的数量之和必须小于该时刻的总空闲车位数。

• 预约保障 —约束条件(22)保证了每个停车人 i在 DR(K)中必须保留其分配。请注意，此处未提及 SR(K)中的停车者。这是因为静态停车者（根据目标函数的定义）仅分配一次，一旦分配后便不会再进入分配系统，因此他们的预约保障也自然成立。

• 费用保障 —所有类型的预订系统都必须遵守其向客户提供的报价或报价承诺，这正是约束条件(24)所实现的目标。系统将在每次决策时间 K记录所有停车者的成本 J，并确保不会将任何停车者重新分配到成本高于 J(K −1)的资源 j上。另请注意，该约束中未提及 SR(K)；因为静态停车者会选择他们希望占用的首选资源j，因此该停车者的 J值将永远不会改变。

• 公平性 —约束条件(23)表明，如果停车人 i相对于停车人 m更靠近其可行资源 Fi(K)，即满足τmj( K)> τij( K)，且停车人 i和 m请求相同的停车类型，则应优先分配给停车人 i，使得当 xi j( K) = 0时， xmj( K)必须设为0。

为了进一步通过“动态”停车者最大化资源利用率，引入了约束条件（25），其中我们定义t0(K)为停车人必须距离目的地 t0(K)更远才能符合动态分配资格的阈值。t0( K)根据表二中的规则，依据实时资源利用率动态地设定。

C. 动态定价引擎

我们还研究了基于每个资源的实时利用率数据 j，以实时方式动态调整占用车位的价格，而不是每隔几天或几个月根据历史数据进行调整。动态定价引擎将每隔预设分钟运行一次，根据表二中的规则更新价格。

表二的使用方式如下：如果一项资源 j = 1在某一时刻 K=1的所有停车位均为空闲状态且原始价格

C01，此时的车位价格将被设定为 C1(K) = 0.25 ∗C01，因为利用率为0%。现在如果利用率上升到60%，系统会将价格提高至全额原始价格 C01。同样，当利用率进一步增加时，价格会上涨至最高（原始价格的200%）；而当利用率下降时，价格将降至最低（原始价格的25%）。

动态定价的动机是在所有停车资源中引入利用率和收入的公平平衡，从而有助于减少整体交通拥堵。需要注意的是，价格变动仅对等待队列中的停车人产生影响。这意味着，已经获得预约或占用停车位的停车人，将按其预约/占用时所确定的固定费率支付费用。

为了在实际中实现这一点，对于不使用iParker的驾驶员，应在停车资源附近部署可变信息标志（VMSs），以显示最新价格信息以及下次价格更新的时间。

D. 算法与实现

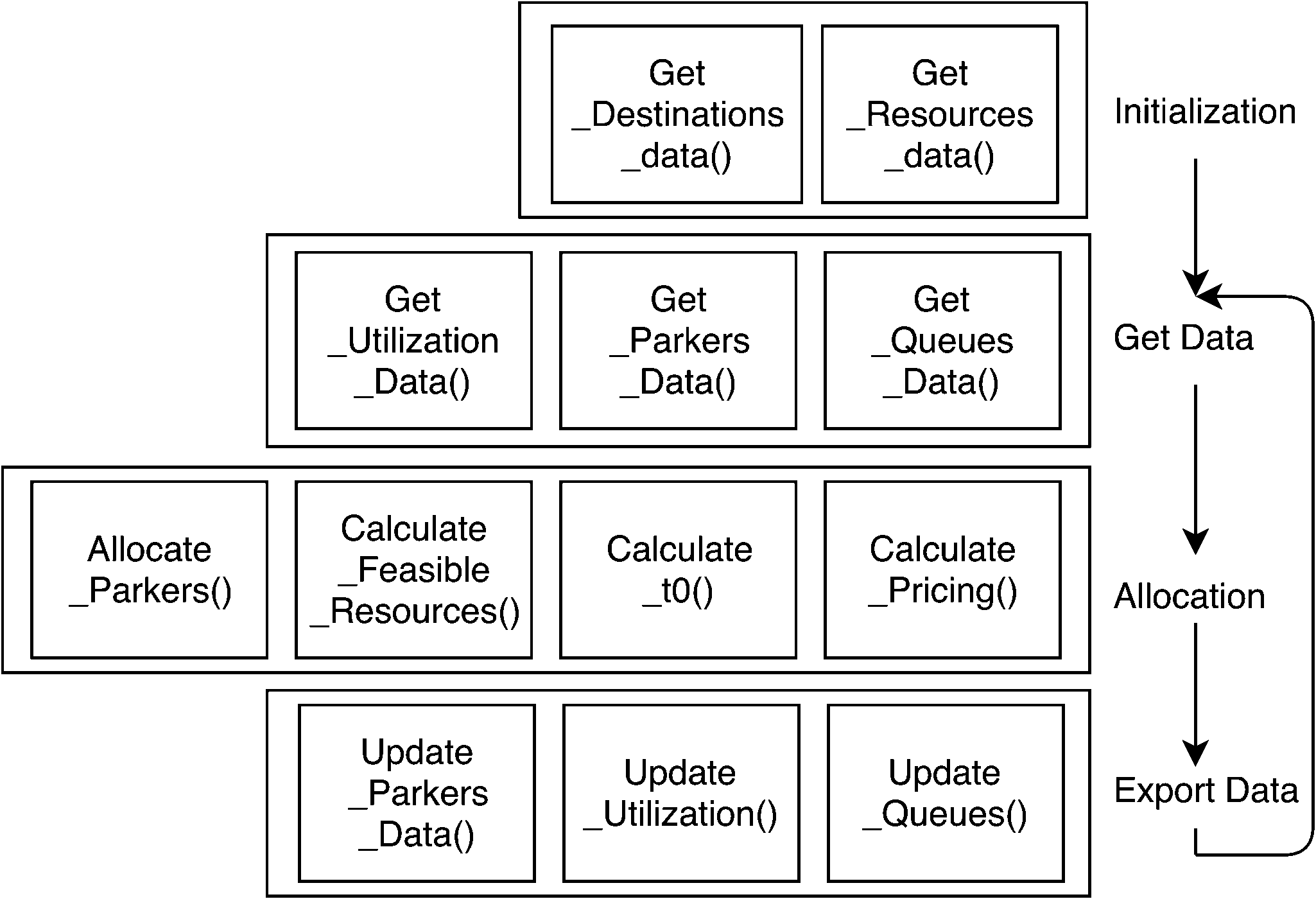
用于求解混合整数线性规划（MILP）问题的软件是 IBM ILOG CPLEX（CPLEX）。为了评估系统有效性，首先对多组数据进行随机化处理，以表示停车者、资源、目的地和定价的数据。使用 Microsoft Excel 生成符合泊松分布的停车者到达数据，其余参数则按指数分布生成。随后创建一个数据库，用于存储这些随机数据，并作为 CPLEX程序的存储节点。如图4所述的CPLEX程序输入先前生成的随机数据，并在停车者分配后更新数据库。

V. 结果与讨论

性能指标：从停车人的角度来看，智能停车应降低成本（无论是金钱、步行距离还是寻找时间，或全部）。另一方面，从停车场管理者的角度来看，智能停车应提供最高的资源利用率并产生最高收入。因此我们定义以下主要性能指标：

• 总利用率 —指资源的平均总利用率，我们将其表示为 U_avg。在仿真结果中，我们进一步将其细分为停车 (UP)、预约(UR)、普通停车人(U_Normal_avg)和残障停车人(U_Disabled_avg)的利用率。
• 收入 —指产生的总收入，在仿真中我们将其细分为道路内和路外收入。
• 寻找时间 —指停车人从到达目的地到实际占用停车位之间的平均耗时。
• 总成本 —指最终成功占用停车资源的停车人所产生的平均总成本，其公式可表示为TotalCost =(1/3)(2(swi(Mij( K)/Mi)+(1 −swi)(Dij(K)/Di)) +(SearchingTimei(K)K/SearchingTimemax))。
• 徘徊率 —指已到达目的地但未能找到或被分配到可用停车资源的停车者所占的比率。

通过在任意指标后添加“−on”或“−off”，我们分别表示路内和路外。同时请注意，“D”指代“动态”，“S”指代“静态”。

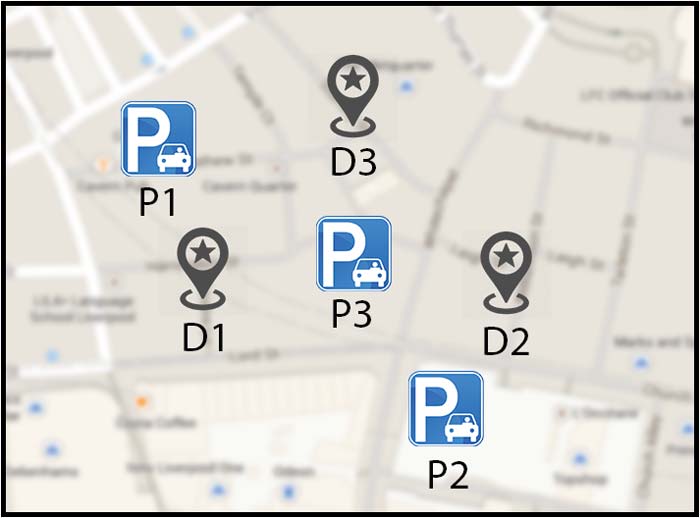
仿真设置：在本节中，iParker系统表示为智能停车 (SP)，引导系统表示为(G)，非引导系统表示为(NG)。G被建模为一个智能停车系统，但不包含预约功能，其描述如下：停车人知晓停车资源的实时可用性、定价及其与目标目的地的接近度。G中的停车人将与SP中一样，尽可能降低其成本。至于NG系统，停车人对停车资源的可用性或价格信息一无所知。在NG系统中，停车者将采用半径递增的方法搜索可接受的空闲停车资源，直至找到并占用该资源。所有仿真将使用表III中的数值（参见图5中的仿真实例环境）。

可扩展性：混合整数线性规划问题属于NP难问题，求解时间与问题复杂度高度相关。此外，随着停车者在较远的未来进行资源预约，我们问题中的静态分配部分将变得更加耗时。在本问题中，关键是在每个决策点的合理时间间隔内获得解决方案。因此，考虑采用以下策略来减小问题规模，并在后续仿真中予以实施：1）分组：通过将资源进行分组，可以显著减少资源数量，使得一个资源包含多个停车位（例如，一个停车场或一条道路）。类似地，位置相近的目的地也可以进行分组。2）区域划分：如果资源和目的地的数量仍然非常大，可以将区域划分为若干子区域，针对每个子区域分别求解问题。3）预约控制：可通过区分距离目的地较远的用户来限制动态预约；而静态预约则可通过缩短停车者可预约车位的时间范围（例如 1周）来进行限制。

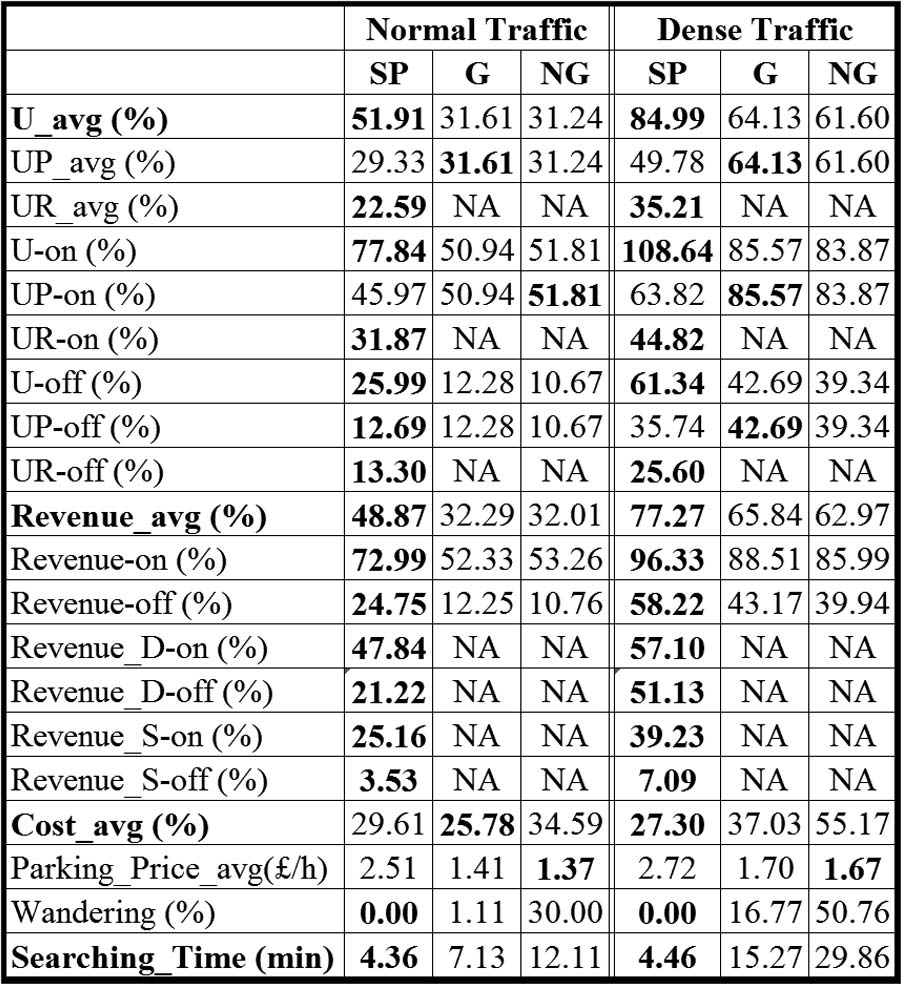
A. 仿真结果 I：均匀到达率

表IV中的结果证明了我们系统背后的概念。从停车场管理者的角度来看，总平均利用率提高了21%，与非引导式系统和引导式系统相比，收入分别增加了16%和14%。尽管其他系统中按停车场计算的利用率（记为UP）高于 SP系统，但由于引入了动态和静态预约，SP系统的总利用率最高。动态变化 t 0( K)的影响可以从结果中看出，在密集交通情况下，SP系统的U‐on低于G系统和NG系统。我们预期会出现这种情况，这是由(25)式的定义决定的。当停车位接近饱和时， t 0( K)趋近于零。在密集交通条件下，路侧停车更容易快速发生这种情况，因为它们比路外停车便宜得多，因此SP系统会将到达的车辆分配至路外停车，直到路边停车利用率下降。然而，这可以被视为一种优势，因为它在不同停车资源之间引入了良好的利用率平衡，进而平衡了整体交通流。

另一方面，从停车者的角度来看，SP系统相比G系统和NG系统能够为停车者提供最低的综合成本。例如，在密集交通情况下，其总成本分别比NG系统和G系统降低了28%和10%。尽管由于预约机制，SP系统在金钱成本上高于其他系统，但使用SP系统的停车者整体满意度更高。这一点在密集交通情况下的结果中表现得尤为明显：与 NG系统相比，SP系统的寻找时间减少了约25分钟，与 G系统相比减少了约11分钟。G系统在密集交通下寻找时间增加的主要原因是“多辆车追逐同一车位”的现象。NG系统寻找时间的显著增加则是由于其盲目寻找可用停车位所致。此外，SP系统还因徘徊时间为零（即停车人到达目的地后未找到可用停车位所耗费的时间）而具有最低的成本。在密集交通情况下，NG系统停车者的徘徊率比正常交通情况下增加了约20%，G系统则增加了约16%。

B. 仿真结果 II：可变到达率

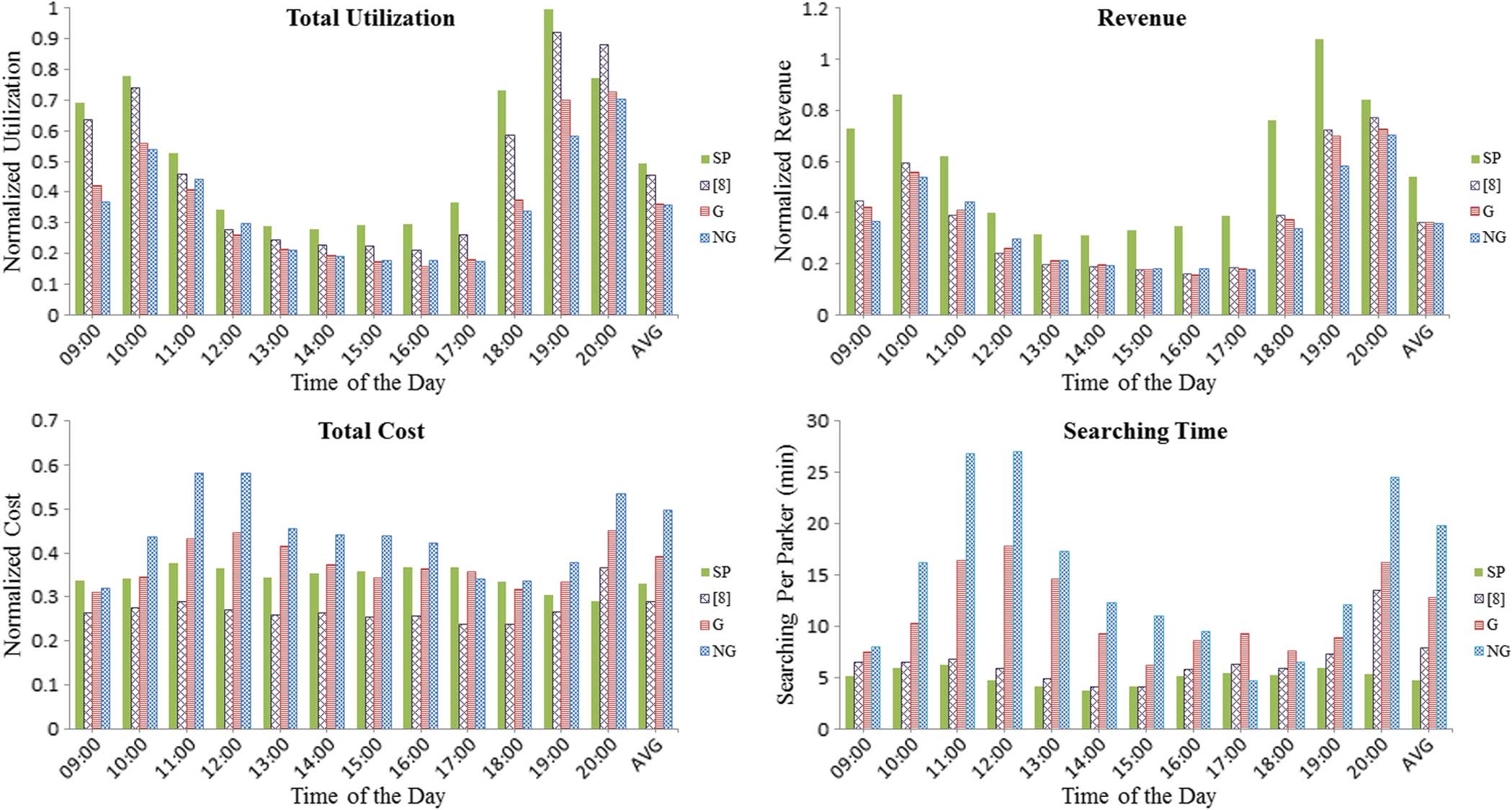
iParker的优势在图6中更加直观，我们在该图中进行了另一次仿真，模拟了从早晨和傍晚的高到达率到下午的低到达率的变化情况。第二次仿真结果与第一次仿真结果一致，均在最大化停车资源利用率、增加收入以及最小化停车者成本方面表现优异。

但需要注意以下几点：1）SP系统在晚上7点的收入大于1。当停车资源接近完全占用时，这种情况通常可能发生，尤其是考虑到预约费用是额外增加的。2）在到达率较低的时间段，SP系统中停车者的总成本相比G系统并未降低。这是因为在G系统中，成本的最小化方式与SP系统完全相同，而当到达率较低时，G系统中的徘徊率接近于零，因此寻找时间最少。然而，这个问题可以通过在到达率较低时段降低预约费用来解决。3）SP系统中的寻找时间在全天基本保持恒定，这证实了我们的模型不允许用户徘徊，从而减少了整体交通拥堵。

我们将我们的系统与[8]的系统进行了比较，结果如图6所示，我们的模型平均利用率高出约5%，寻找时间减少40%，收入增加18%。利用率和收入的提升明显是因为我们的模型允许静态预约，并且动态预约的预订时间阈值不是固定的，不像[8]中那样。最后，总停车人成本增加了4%，这是因为在[8],中他们不收取预订费用。这些结果表明，我们的模型确实优于[8]中的模型。

仿真中使用的大多数参数被设置为动态的，而非固定不变，除了用于设置动态预约资源与静态预约资源之间比率的参数（DR:SR）之外。表V显示了在不同到达率下，不同DR:SR情况的主要性能指标。表格显示DR:SR=70: 30取得了最佳结果。其原因是停车者的到达率如表III所示被设定为70:30。然而观察到的变化可以忽略不计。这证明了前文讨论的动态‐静态接口具有良好的效率。因此，将DR:SR= 50:50作为默认设置是合理的，因为在现实世界中，停车者在动态预约和静态预约之间的选择不会保持恒定。

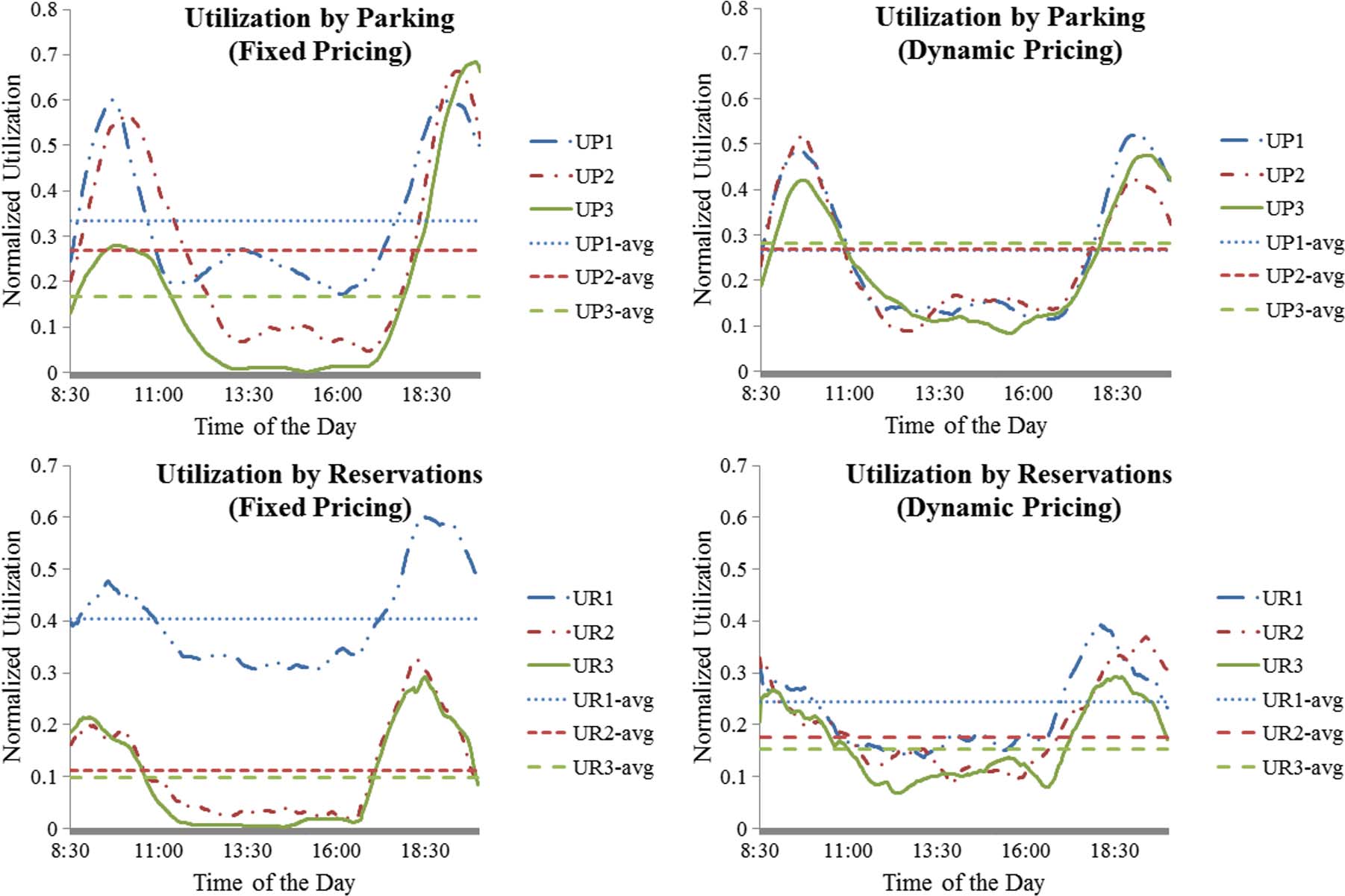
C. 仿真结果 III：固定定价 vs. 动态定价

在本节中，我们探讨了根据表二中的方案，利用实时利用率测量动态调整资源定价的影响，并在图7中展示了结果。可以观察到，正如预期的那样，通过持续改变资源价格，我们能够控制并限制这些资源的利用率。此外，这些变化导致停车资源之间的利用率实现了公平平衡，从而有助于减少由停车引起的整体交通拥堵。使用固定定价时，停车资源1的平均利用率高于其他资源；而使用动态定价时则发生了显著变化，使得3个停车资源的平均利用率接近相同。

VI. 结论与未来工作

在本文中，我们提出了iParker，一种基于混合整数线性规划（MILP）模型的新型智能停车系统，该模型可为停车者动态和静态分配停车资源提供最优解，并提供灵活的预约选项。本文引入的新概念包括：实时预约与共享时段预约的结合，根据实时利用率信息动态执行系统决策（预约时间约束和定价），以及为驾驶员提供选择多个目的地和预约类型的权利。我们还提出了针对静态和动态预约的定价策略，以最大化停车收入。大量仿真结果表明，与无引导停车系统相比，所提出的系统显著降低了所有停车者的总有效成本达28%，总利用率最高提升21%，停车管理的总收入最高增加16%。最后，我们提出了一种动态定价方案，通过将其集成到iParker模型中，仿真发现该方案能够平衡所有停车资源的利用率，从而有助于消除因停车引起的整体交通拥堵。

目前，研究重点集中在新的停车感应基础设施和用于停车场的室内导航服务。未来，我们旨在利用实时数据以及更多数量的资源和目的地来评估我们的系统。此外，还将进行可扩展性分析，以检验所提出的可扩展性技术的效率。最后，模拟现实生活中不同的停车到达场景也将是有用的。