数据结构 二叉堆 & 堆排序

二叉堆，是一个满二叉树，满足堆的性质。即父节点大于等于子节点（max heap）或者是父节点小于等于子节点（min heap）。二叉堆的如上性质常用于优先队列（priority queue）或是用于堆排序。

由于max heap 与min heap类似，下文只针对min heap进行讨论和实现。

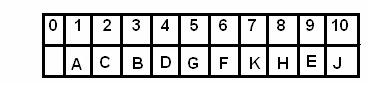
如上图，是根据字母的ASCII码建立的最小堆。

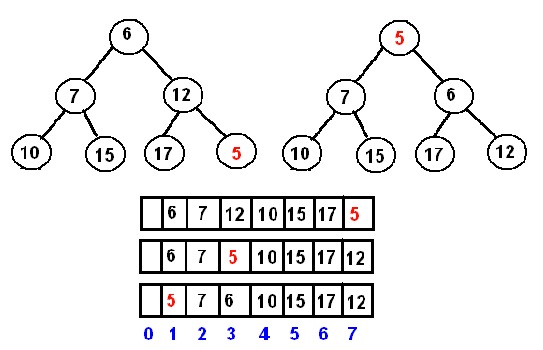
我们用数组对满二叉树采用宽度优先遍历存储堆结构，如下图所示：

从数组下标1开始存储堆，这样的处理方式可以得到如下性质：

1.堆中的每个父节点k，他的两个子节点为k*2和k*2+1

2.堆中的每个子节点k，他的父节点为k/2

堆的插入：当向堆中插入一个元素时，首先将新添加的元素放入数组的末尾，然后使用percolatingUp方法，将新添加的元素逐层向上移动至合适位置。如下图所示：

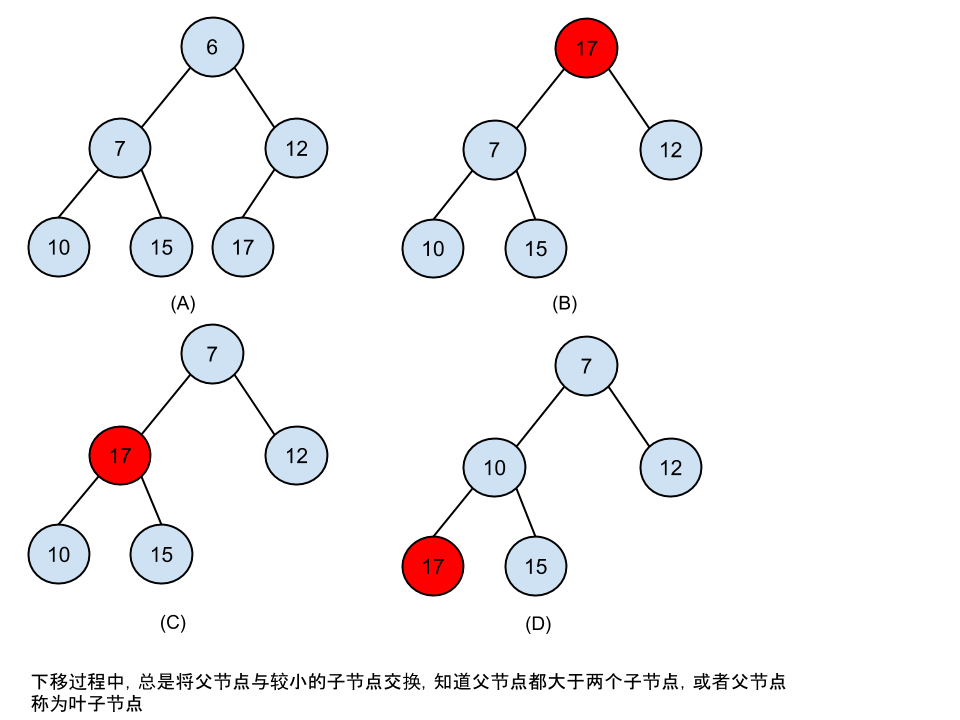
堆的删除：当将堆顶元素删除时，首先将数组中末尾的元素放入对顶，然后使用percolatingDown方法，将堆顶元素逐层向下移动至合适位置。如下图所示：

堆的构建：将对大小为k的数组，从第k/2个元素开始（第1个到第k/2个元素有子节点），依次使用porcelatingUp将元素向上调整，其时间复杂度O(k)。

堆排序的思想是：将待排序的数组转成堆（堆的构建），删除root节点（获取最小元素)，重构(porcelatingDown),删除root节点（获取第二小元素）,重构（porcelatingDown),...一直到堆中不再有元素。

堆操作的时间复杂度(N表示元素个数)：

建堆：O(N)

添加：O(logN)

删除：O(logN)

堆排序：O(NlogN)

堆及堆排序的java实现：

/****************************************************************************
 *       This demonstrates binary heap operations along with the heapSort.
 *
 *****************************************************************************/
import java.util.*;

@SuppressWarnings("unchecked")
public class Heap<AnyType extends Comparable<AnyType>>
{
   private static final int CAPACITY = 2;

   private int size;            // Number of elements in heap
   private AnyType[] heap;     // The heap array

   public Heap()
   {
      size = 0;
      heap = (AnyType[]) new Comparable[CAPACITY];
   }

 /**
  * Construct the binary heap given an array of items.
  */
   public Heap(AnyType[] array)
   {
      size = array.length;
      heap = (AnyType[]) new Comparable[array.length+1];

      System.arraycopy(array, 0, heap, 1, array.length);//we do not use 0 index

      buildHeap();
   }
 /**
  *   runs at O(size)
  */
   private void buildHeap()
   {
      for (int k = size/2; k > 0; k--)
      {
         percolatingDown(k);
      }
   }
   private void percolatingDown(int k)
   {
      AnyType tmp = heap[k];
      int child;

      for(; 2*k <= size; k = child)
      {
         child = 2*k;

         if(child != size &&
            heap[child].compareTo(heap[child + 1]) > 0) child++;

         if(tmp.compareTo(heap[child]) > 0)  heap[k] = heap[child];
         else
                break;
      }
      heap[k] = tmp;
   }

 /**
  *  Sorts a given array of items.
  */
   public void heapSort(AnyType[] array)
   {
      size = array.length;
      heap = (AnyType[]) new Comparable[size+1];
      System.arraycopy(array, 0, heap, 1, size);
      buildHeap();

      for (int i = size; i > 0; i--)
      {
         AnyType tmp = heap[i]; //move top item to the end of the heap array
         heap[i] = heap[1];
         heap[1] = tmp;
         size--;
         percolatingDown(1);
      }
      for(int k = 0; k < heap.length-1; k++)
         array[k] = heap[heap.length - 1 - k];
   }

 /**
  * Deletes the top item
  */
   public AnyType deleteMin() throws RuntimeException
   {
      if (size == 0) throw new RuntimeException();
      AnyType min = heap[1];
      heap[1] = heap[size--];
      percolatingDown(1);
      return min;
	}

 /**
  * Inserts a new item
  */
   public void insert(AnyType x)
   {
      if(size == heap.length - 1) doubleSize();

      //Insert a new item to the end of the array
      int pos = ++size;

      //Percolate up
      for(; pos > 1 && x.compareTo(heap[pos/2]) < 0; pos = pos/2 )
         heap[pos] = heap[pos/2];

      heap[pos] = x;
   }
   private void doubleSize()
   {
      AnyType [] old = heap;
      heap = (AnyType []) new Comparable[heap.length * 2];
      System.arraycopy(old, 1, heap, 1, size);
   }

   public String toString()
   {
      String out = "";
      for(int k = 1; k <= size; k++) out += heap[k]+" ";
      return out;
   }

   public static void main(String[] args)
   {
      Heap<String> h = new Heap<String>();

      h.insert("p");
      h.insert("r");
      h.insert("i");
      h.insert("o");
      System.out.println(h);
      h.deleteMin();
      System.out.println(h);


      Heap<Integer> tmp = new Heap<Integer>();
      Integer[] a = {4,7,7,7,5,0,2,3,5,1};
      tmp.heapSort(a);
      System.out.println(Arrays.toString(a));
   }
}

参考：

1.http://www.cs.cmu.edu/~adamchik/15-121/lectures/Binary%20Heaps/heaps.html

2.http://en.wikipedia.org/wiki/Binary_heap