【考研】（转载）考研数学高数公式知识点整理

前言：本人考数二，故只整理了公共部分。数一、三单独考察部分未整理。除必会公式外，还收录了自己做题中较常见的部分公式。

注：在1920x1080分辨率下，Edge浏览器可能会导致公式中部分“-”号显示异常，请调整缩放比至110%及以上，或使用其他浏览器。

由于本人考数二，恕其他部分无暇顾及，其次，本文只是笔记，故不会涵盖所有知识点。
已停更，暂无打印版，本文所有数学公式均为Latex手打，想打印的可以自己想办法复制出来拍一下版。

已更新内容：

• 函数极限与连续
• 数列极限
• 导数相关
• 积分相关
• 三角函数相关
• 不等式相关
• 多元函数
• 其他公式
• 复合函数相关
• 二重积分
• 微分方程
• 各种应用公式
• 隐藏条件

一、函数极限与连续

泰勒公式

$$\begin{gathered} sinx=x-\frac{x^3}{3!}+o(x^3)arcsinx=x+\frac{x^3}{3!}+o(x^3) \\ tanx=x+\frac{x^3}{3}+o(x^3)arctanx=x-\frac{x^3}{3}+o(x^3) \\ cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}+o(x^4)(1+x{)}^{\alpha }=1+\alpha x+\frac{\alpha (\alpha -1)}{2!}{x}^2+o(x^2) \\ {e}^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+o(x^3)ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+o(x^3) \end{gathered}$$

判断是否正负相间技巧：
若图像爆炸式增长，则恒正，如 ：
$$e^x$$
若图像上下波动或增长缓慢，则正负相间，如：
$$sinx、cosx$$

麦克劳林公式

$$\begin{gathered} e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\cdots +\frac{x^n}{n!}+o(x^n) \\ \sin x=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}=x-\frac{x^3}{6}+o(x^3) \\ \cos x=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n)!}{x}^{2n}=1-\frac{1}{2}{x}^2+o(x^2) \\ \ln (1+x)=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{n+1}{x}^{n+1}=x-\frac{1}{2}{x}^2+o(x^2) \\ (1+x{)}^{\alpha }=1+\sum _{n=1}^{\infty }\frac{\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}{x}^n=1+\alpha x+\frac{\alpha (\alpha -1)}{2!}{x}^2+o(x^2) \\ \arctan x=x-\frac{1}{3}{x}^3+o(x^3) \\ \tan x=x+\frac{1}{3}{x}^3+o(x^3) \\ \arcsin x=x+\frac{1}{6}{x}^3+o(x^3) \end{gathered}$$

常用等价无穷小

$$\begin{gathered} sinx\sim tanx\sim arcsinx\sim arctanx\sim x \\ x-sinx\sim \frac{1}{6}{x}^{3}x-arcsinx\sim -\frac{1}{6}{x}^3 \\ x-tanx\sim -\frac{1}{3}{x}^{3}x-arctanx\sim \frac{1}{3}{x}^3 \\ 1-cosx\sim \frac{1}{2}{x}^2(1-co{s}^{a}x\sim \frac{a}{2}{x}^2) \\ {a}^x-1\sim xlna(1+x{)}^a-1\sim ax \\ {e}^x-1\sim xln(1+x)\sim x \end{gathered}$$

注：
$$\begin{gathered} 型如1^{\infty }即I=\lim g(x{)}^{f(x)} \\ 若g(x)\to 1,f(x)\to \infty \\ 则令A=\lim f(x)[g(x)-1] \\ I=e^A \end{gathered}$$

比阶：
$$\begin{array}{rl}若x\to 0时，f(x)和g(x)分别是x的m、n阶无穷小,则：& \\ & 1、f(x)g(x)是x的m+n阶无穷小\\ & 2、若m>n，\frac{f(x)}{g(x)}是x的m-n阶无穷小\\ & 3、m>n时，f(x)\pm g(x)是x的n阶无穷小；\\ & 4、m=n时，f(x)\pm g(x)是x的n阶或高于n阶无穷小;\\ & 5、{\int }_0^{g(x)}f(t)dt是x的(m+1)\cdot n阶无穷小\end{array}$$

增长速度：
$$x\to \infty 时，a<lo{g}_{a}x<x<a^x<x!<x^x$$

洛必达易错点：
$$\begin{array}{rl}& 1、对\frac{0}{0}、\frac{\infty }{\infty }型可使用洛必达，若结果不存在，则洛必达失效，应使用其他方法。\\ & \\ & 2、若f(x)在x=0处无定义，如f(x)=\frac{1}{x},则对\underset{x\to 0}{\lim }\frac{{\int }_0^{x}f(t)dt}{x}不能使用洛必达\\ 原因：对变限积分{\int }_a^{x}f(t)dt求导的前提：在[a,x]内连续& \\ & 3、f(x)在某处存在二阶导数\nRightarrow f(x)二阶导数连续\\ 即对于\underset{x\to 0}{\lim }\frac{f^{\prime }(x)}{x}不能使用洛必达& \end{array}$$

其他结论：
1 、 { a m p ; lim ⁡ n → + ∞ a 1 n + a 2 n + ⋯ + a m n n = m a x { a 1 , a 2 ⋯   , a m } a m p ; lim ⁡ n → − ∞ a 1 n + a 2 n + ⋯ + a m n n = m i n { a 1 , a 2 ⋯   , a m } （ a 1 … a m 都 是 非 负 数 ） 2 、 ∫ 0 + ∞ e − x 2 d x = π 2 3 、 lim ⁡ n → ∞ a n = 1 ( a > 0 ) \begin{aligned} &1、 \left\{ \begin{aligned} &amp;\lim_{n \rightarrow +\infty}{\sqrt[n]{a_1^n+a_2^n+\cdots+a_m^n}}=max\{a_1,a_2\cdots,a_m\} \\ &amp;\lim_{n \rightarrow -\infty}{\sqrt[n]{a_1^n+a_2^n+\cdots+a_m^n}}=min\{a_1,a_2\cdots,a_m\} \end{aligned} \right. （a_1\dots a_m都是非负数） \\ &2、\int_0^{+\infty} e^{-x^2}dx=\frac{\sqrt{\pi}}{2}\\ &3、\lim_{n \rightarrow \infty}{\sqrt[n]{a}=1} \qquad (a>0) \end{aligned} ​1、⎩⎨⎧​​amp;n→+∞lim​na1n​+a2n​+⋯+amn​ ​=max{a1​,a2​⋯,am​}amp;n→−∞lim​na1n​+a2n​+⋯+amn​ ​=min{a1​,a2​⋯,am​}​（a1​…am​都是非负数）2、∫0+∞​e−x2dx=2π ​​3、n→∞lim​na ​=1(a>0)​

二、数列极限

单调性
1、利用基本不等式

$$2、把x_n改为x，引入f(x)证明数列单调$$
{ 若 f ′ ( x ) > 0 ， 则 { x n } 单 调 { 当 x 2 > x 1 时 ， { x n } 单 调 增 加 当 x 2 < x 1 时 ， { x n } 单 调 减 小 f ′ ( x ) < 0 时 ， 则 { x n } 不 单 调 \begin{aligned} \left\{ \begin{aligned} &若f'(x)>0，则\{x_n\}单调\left\{ \begin{aligned} 当x_2>x_1时，\{x_n\}单调增加\\ 当x_2<x_1时，\{x_n\}单调减小\\ \end{aligned} \right.\\\\ & f'(x)<0时，则\{x_n\}不单调 \end{aligned} \right. \end{aligned} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​​若f′(x)>0，则{xn​}单调{当x2​>x1​时，{xn​}单调增加当x2​<x1​时，{xn​}单调减小​f′(x)<0时，则{xn​}不单调​​

三、导数相关

基本求导公式：
$$\begin{gathered} (x^{\alpha }{)}^{\prime }=\alpha x^{\alpha -1},(a^x{)}^{\prime }=a^{x}lna，(e^x{)}^{\prime }=e^x，(lo{g}_{a}x{)}^{\prime }=\frac{1}{xlna}，(lnx{)}^{\prime }=\frac{1}{x} \\ (sinx{)}^{\prime }=cosx，(cosx{)}^{\prime }=-sinx，(arcsinx{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}，(arccosx{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}} \\ (tanx{)}^{\prime }=se{x}^{2}x，(cotx{)}^{\prime }=-cs{c}^{2}x，(arctanx{)}^{\prime }=\frac{1}{1+x^2}，(arccotx{)}^{\prime }=-\frac{1}{1+x^2} \\ (secx{)}^{\prime }=secxtanx，(cscx{)}^{\prime }=-cscxcotx \end{gathered}$$

特殊求导：
$$\begin{array}{rl}& (ln|x|{)}^{\prime }=\frac{1}{x}ln|x|求导可视绝对值而不见\\ & (e^x+e^{-x}{)}^{\prime \prime }=e^x+e^{-x}\\ & [ln(x+\sqrt{a^2+x^2}){]}^{\prime }=\frac{1}{\sqrt{a^2+x^2}}（ln(x+\sqrt{1+x^2})为奇函数）\end{array}$$

导数定义
$$\begin{array}{rl}& f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}\\ & f^{\prime }(a)=\underset{x\to a}{\lim }\frac{f(x)-f(a)}{x-a}\\ & \Delta y=A\Delta x+o(\Delta x)（线性主部：A\Delta x=dy=y_x^{\prime }\Delta x）\end{array}$$

高阶求导公式

$$(e^{ax+b}{)}^{(n)}=a^n{e}^{ax+b}$$
$$[sin(ax+b){]}^{(n)}=a^{n}sin(ax+b+\frac{n}{2}\pi )$$
$$[cos(ax+b){]}^{(n)}=a^{n}cos(ax+b+\frac{n}{2}\pi )$$
$$[ln(ax+b){]}^{(n)}=(-1{)}^{n-1}{a}^n\frac{(n-1)!}{(ax+b{)}^n}$$
$$(\frac{1}{a+bx}{)}^{(n)}=(-1{)}^n{b}^n\frac{n!}{(a+bx{)}^{n+1}}$$
$$(\frac{1}{a-bx}{)}^{(n)}=b^n\frac{n!}{(a-bx{)}^{n+1}}$$

$$扩展：题目可以出成f(x,y)对x求n阶偏导$$

子孙三代的关系

$$\begin{gathered} {\int }_0^{x}f(x)dx⟵f(x)⟶f^{\prime }(x) \\ 奇\stackrel{①}{⟵}偶⟶奇 \\ 偶⟵奇⟶偶 \\ T\stackrel{②}{⟵}T⟶T \end{gathered}$$
$$\begin{array}{rl}& ①当且仅当下限为0时成立\\ & ②当且仅当{\int }_0^{T}f(x)dx=0时成立\end{array}$$

带拉格朗日余项的 n 阶泰勒公式

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\cdots +\frac{1}{n!}{f}^{(n)}(\xi )(x-x_0{)}^n（\xi 介于x,x_0之间）$$

其他结论

$$\begin{array}{r}1、g(x)在a处连续,若f(x)=|x-a|g(x)在x=a处可导，则g(a)=0\\ \end{array}$$
$$\begin{array}{rl}& 2、若f(x)在x=0处连续，且\underset{x\to 0}{\lim }\frac{f(x)}{x}=A\\ & 则：①f(0)=0。②f^{\prime }(0)=A。\end{array}$$
$$\begin{array}{rl}3、& 不定积分存在定理\\ & ①f(x)在区间I上连续⟶f(x)在I上有原函数。\\ & ②f(x)在区间上有第一类间断点、无穷间断点⟶f(x)在I上不存在原函数。\end{array}$$
$$\begin{array}{rl}4、& 定积分存在定理\\ & \\ & amp;充分条件:\\ & ①f(x)在区间[a,b]上连续⟶F(x)={\int }_a^{b}f(x)dx存在\iff f(x)在[a,b]可积\\ & amp;②f(x)在区间[a,b]上单调⟶F(x)={\int }_a^{b}f(x)dx存在\iff f(x))在[a,b]可积\\ & amp;③f(x)在区间[a,b]上有界，且只有有限个间断点⟶F(x)={\int }_a^{b}f(x)dx存在\iff f(x)在[a,b]可积\\ & \\ & amp;必要条件:\\ & amp;①可积函数必有界，即若定积分F(x)={\int }_a^{b}f(x)dx存在，则f(x)在[a,b]上必有界。\end{array}$$

$$\begin{array}{rl}5、& 变限积分的性质：\\ & ①函数f(x)在[a,b]上可积，则F(x)={\int }_a^{x}f(t)dt在[a,b]连续。\\ & ②函数f(x)在[a,b]上连续，则F(x)={\int }_a^{x}f(t)dt在[a,b]可导。\end{array}$$

三、积分相关

基本积分公式

$$关于a^2和x^2积分$$

$$\begin{gathered} \int \frac{1}{x^2+a^2}dx=\frac{1}{a}arctan\frac{x}{a}+C \\ \int \frac{1}{x^2-a^2}dx=\frac{1}{2a}\ln |\frac{x-a}{x+a}|+C \end{gathered}$$

$$\begin{gathered} \int \frac{1}{\sqrt{x^2+a^2}}dx=\ln (x+\sqrt{x^2+a^2})+C \\ \int \frac{1}{\sqrt{x^2-a^2}}dx=\ln |x+\sqrt{x^2-a^2}|+C \\ \int \frac{1}{\sqrt{a^2-x^2}}dx=arcsin\frac{x}{a}+C \end{gathered}$$

$$\begin{gathered} \int \sqrt{x^2+a^2}dx=\frac{x}{2}\sqrt{x^2+a^2}+\frac{a^2}{2}\ln (x+\sqrt{x^2+a^2})+C \\ \int \sqrt{x^2-a^2}dx=\frac{x}{2}\sqrt{x^2-a^2}-\frac{a^2}{2}\ln |x+\sqrt{x^2-a^2}|+C \\ \int \sqrt{a^2-x^2}dx=\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \frac{x}{a}+C \end{gathered}$$

关于三角函数积分

$$\begin{gathered} \int secxdx=\ln |secx+tanx|+C \\ \int cscxdx=\ln |cscx-cotx|+C \end{gathered}$$

$$\begin{gathered} \int se{c}^{2}xdx=tanx+C \\ \int cs{c}^{2}xdx=-cotx+C \end{gathered}$$

$$\begin{gathered} \int secxtanxdx=secx+C \\ \int cscxcotxdx=-cscx+C \end{gathered}$$

$$\begin{gathered} \int si{n}^{2}xdx=\frac{1}{2}x-\frac{1}{4}sin2x+C \\ \int co{s}^{2}xdx=\frac{1}{2}x+\frac{1}{4}sin2x+C \end{gathered}$$

$$\begin{gathered} \int ta{n}^{2}xdx=tanx-x+C \\ \int co{t}^{2}xdx=-cotx-x+C \end{gathered}$$

Wallis（华里士）公式及相关

$$I_n={\int }_0^{\frac{\pi }{2}}si{n}^{n}xdx=\{\begin{array}{rl}& amp;\frac{n-1}{n}\cdot \frac{n-3}{n-2}\cdot \cdot \cdot \frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi }{2}n为正偶数\\ & \\ & amp;\frac{n-1}{n}\cdot \frac{n-3}{n-2}\cdot \cdot \cdot \frac{4}{5}\cdot \frac{2}{3}\cdot 1n为正奇数\end{array}$$

$$\begin{array}{r}\{\begin{array}{rl}& {\int }_0^{\frac{\pi }{2}}si{n}^{n}xdx={\int }_0^{\frac{\pi }{2}}co{s}^{n}xdx\\ & \\ & {\int }_0^{\pi }si{n}^{n}xdx=2{\int }_0^{\frac{\pi }{2}}si{n}^{n}xdx\\ & {\int }_0^{\pi }co{s}^{n}xdx=\{\begin{array}{rlrl}& 0& & n为正奇数\\ & 2{\int }_0^{\frac{\pi }{2}}co{s}^{n}xdx& & n为正偶数\end{array}\\ & \\ & {\int }_0^{2\pi }si{n}^{n}xdx={\int }_0^{2\pi }co{s}^{n}xdx=\{\begin{array}{rlrl}& 0& & n为正奇数\\ & 4{\int }_0^{\frac{\pi }{2}}co{s}^{n}xdx& & n为正偶数\end{array}\\ & \end{array}\end{array}$$

$${\int }_0^{\pi }xf(sinx)dx=\frac{\pi }{2}{\int }_0^{\pi }f(sinx)dx=\pi {\int }_0^{\frac{\pi }{2}}f(sinx)dx$$

注：
$$\begin{array}{rl}& ①f(sinx)包括f(|cosx|)、f(co{s}^{n}x)dx(n为偶数)\\ & ②有人误以为cosx=\sqrt{1-si{n}^{2}x}可以写成f(sinx)，\\ & 当x\in [0,\pi ]时，cosx\in [-1,1],而\sqrt{1-si{n}^{2}x}=|cosx|\in [0,1]\\ & 显然不成立。\end{array}$$

做题常见积分

$$\begin{array}{r}\int xsinxdx=-xcosx+sinx+C\\ \int xcosxdx=xsinx+cosx+C\end{array}$$
$$\int lnxdx=xlnx-x+C$$

$$\int xlnxdx=\frac{1}{2}{x}^{2}lnx-\frac{1}{4}{x}^2+C$$

$$\int x{e}^{x}dx=x{e}^x-e^x+C$$

$$\int sin2xdx=si{n}^{2}x+C$$

$$\int \frac{f^{\prime }(x)}{f(x)}dx=ln|f(x)|+C(常用于构造辅助函数)$$

反常积分的判敛

$$\begin{array}{rl}& amp;①要求每个积分有且仅有一个奇点\\ & amp;②\{\begin{array}{rl}{\int }_1^{+\infty }\frac{1}{x^p}\{\begin{array}{rlr}& amp;p>1时,& amp;收敛\\ & amp;p\le 1,& amp;发散\end{array}& amp;(大的喜欢大的)\\ & \\ {\int }_0^1\frac{1}{x^p}\{\begin{array}{rlr}& amp;0<p<1时,& amp;收敛\\ & amp;p\ge 1,& amp;发散\end{array}& amp;(小的喜欢小的)\end{array}\end{array}$$

其他

$$1、sinx或cosx面积$$

$$\begin{gathered} 2、积分中值定理 \\ {\int }_a^{b}f(x)dx=A,则f(\xi )=\frac{{\int }_a^{b}f(x)dx}{b-a}=\frac{A}{b-a} \end{gathered}$$

四、三角函数相关

相互转化

$$\begin{gathered} 1+ta{n}^{2}x=se{c}^{2}x \\ 1+co{t}^{2}x=cs{c}^{2}x \end{gathered}$$

$$\begin{gathered} sin2x=2sinxcosx \\ \begin{array}{rl}cos2x& =co{s}^{2}x-si{n}^{2}x\\ & =1-2si{n}^{2}x\\ & =2co{s}^{2}x-1\end{array} \end{gathered}$$

$$\begin{gathered} sin3x=-4si{n}^{3}x+3sinx \\ cos3x=4co{s}^{3}x-3cosx \end{gathered}$$
$$\begin{gathered} si{n}^{2}x=\frac{1}{2}(1-cos2x) \\ co{s}^{2}x=\frac{1}{2}(1+cos2x) \end{gathered}$$

变角

$$\begin{gathered} sin(\pi \pm x)=\mp sinx \\ cos(\pi \pm x)=-cosx \\ sin(\frac{\pi }{2}\pm x)=cosx \\ cos(\frac{\pi }{2}\pm x)=\mp sinx \end{gathered}$$

$$asinx+bcosx=\sqrt{a^2+b^2}sin(x+arctan\frac{b}{a})$$

万能公式(不常用)

$$令u=tan\frac{x}{2}$$

$$sinx=\frac{2tan\frac{x}{2}}{1+ta{n}^2\frac{x}{2}}=\frac{2u}{1+u^2}$$

$$cosx=\frac{1-ta{n}^2\frac{x}{2}}{1+ta{n}^2\frac{x}{2}}=\frac{1-u^2}{1+u^2}$$

$$tanx=\frac{2tan\frac{x}{2}}{1-ta{n}^2\frac{x}{2}}=\frac{2u}{1-u^2}$$

$$一般用于解\int \frac{1}{a+sinx}dx、\int \frac{1}{a+cosx}dx、\int \frac{1}{a+sinx+cosx}dx$$
$$\begin{array}{rl}步骤：& ①令u=tan\frac{x}{2},则dx=\frac{2}{1+u^2}du\\ & ②sinx=\frac{2u}{1+u^2}、cosx=\frac{1-u^2}{1+u^2}\end{array}$$
$$若是不定积分，最后别忘代回x$$

和差角公式

$$\begin{gathered} \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\ \sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\ \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\ \cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta \\ \tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta } \\ \tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta } \end{gathered}$$

积化和差（不常用）

$$\begin{gathered} \sin \alpha \cos \beta =\frac{1}{2}[\sin (\alpha +\beta )+\sin (\alpha -\beta )] \\ \cos \alpha \sin \beta =\frac{1}{2}[\sin (\alpha +\beta )-\sin (\alpha -\beta )] \\ \cos \alpha \cos \beta =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )] \\ \sin \alpha \sin \beta =-\frac{1}{2}[\cos (\alpha +\beta )-\cos (\alpha -\beta )] \end{gathered}$$

和差化积（不常用）

$$\begin{gathered} \sin \alpha +\sin \beta =2\sin \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2} \\ \sin \alpha -\sin \beta =2\cos \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2} \\ \cos \alpha +\cos \beta =2\cos \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2} \\ \cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2} \end{gathered}$$

$$\begin{gathered} 特殊方法： \\ 记“帅”=sinx“哥”=cosx \\ 帅+帅=帅哥 \\ 帅-帅=哥帅 \\ 哥+哥=哥哥 \\ 哥-哥=负嫂嫂 \end{gathered}$$

五、不等式

$$|a\pm b|\le |a|+|b|;||a|-|b||\le |a-b|$$

$$\sqrt{ab}\le \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}$$

$$\sqrt[3]{abc}\le \frac{a+b+c}{3}$$

$$sinx<x<tanx(0<x<\frac{\pi }{2})$$

$$arctanx<x<acrsinx(0<x<1)$$

$$e^x\ge x+1x-1\ge lnx$$

$$\frac{1}{1+x}\le ln(1+\frac{1}{x})\le \frac{1}{x}$$

六、多元函数

![在这里插入图片描述](https://img-blog.csdnimg.cn/32c7f6067bf84465b5649f665112dc4d.jpg?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5bCR6I6r5Y2D5Y2O,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)

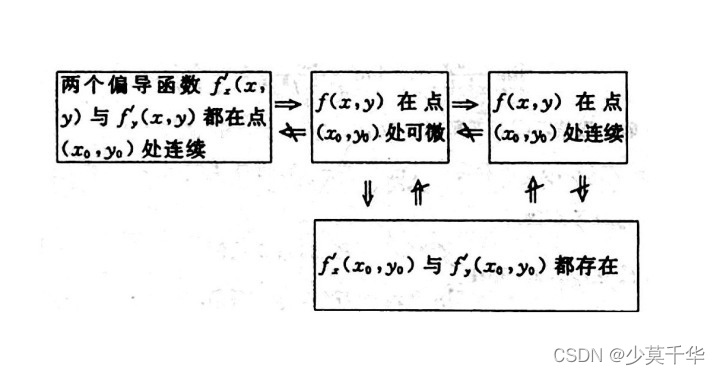
 偏导存在性、可微性
![在这里插入图片描述](https://img-blog.csdnimg.cn/9b4f29f03b0441d1afa58d5b5da1020e.jpg?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5bCR6I6r5Y2D5Y2O,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)

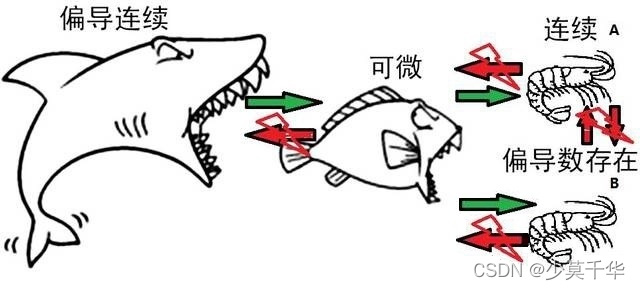
结论：
$$1、f(x,y)为常数\iff \frac{\partial f}{\partial x}\equiv \frac{\partial f}{\partial y}\equiv 0\iff df(x,y)\equiv 0$$

雅可比：
$$\begin{gathered} 设：\{\begin{array}{r}aF(x,y,z)=0,\\ G(x,y,z)=0,\end{array}当满足\frac{\partial (F,G)}{\partial (y,z)}\ne 0时， \\ \frac{dy}{dx}=-\frac{\frac{\partial (F,G)}{\partial (x,z)}}{\frac{\partial (F,G)}{\partial (y,z)}}\frac{dz}{dx}=-\frac{\frac{\partial (F,G)}{\partial (y,x)}}{\frac{\partial (F,G)}{\partial (y,z)}} \end{gathered}$$

七、二重积分

对称性

①普通对称性：
$$\begin{array}{rl}& 若D关于y=x对称，则：\\ & {\iint }_{D}f(x,y)d\sigma =\{\begin{array}{rlr}& 2{\iint }_{D_1}f(x,y)d\sigma ，& f(x,y)=f(y,x)\\ & 0，& f(x,y)=-f(y,x)\end{array}\\ (& D_1是D关于x对称的半个部分)\end{array}$$

②轮换对称性 ：
$$\begin{array}{rl}& 若将D中x,y对调后，D不变，则有则：\\ & I={\iint }_{D}f(x,y)d\sigma ={\iint }_{D}f(y,x)d\sigma \end{array}$$

![在这里插入图片描述](https://img-blog.csdnimg.cn/a5eac7c5aef241518d7e94619582fae2.jpg?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5bCR6I6r5Y2D5Y2O,size_16,color_FFFFFF,t_70,g_se,x_16#pic_center)



    问：谁动了你的面包？答：没人动 ——宇哥

八、微分方程

结论

$$\begin{gathered} 1、如果y_1,y_2,y_3是二阶非齐次线性微分方程的3个解， \\ 则:当且仅当a+b+c=1时，a{y}_1+b{y}_2+c{y}_3是该方程的通解 \end{gathered}$$

九、各种应用公式

1.面积

$$\begin{gathered} 直角坐标：S={\int }_a^b|f(x)-g(x)|dx \\ 极坐标：S={\int }_{\alpha }^{\beta }\frac{1}{2}|r_2^2(\theta )-r_1^2(\theta )|d\theta \end{gathered}$$

2.平面曲线弧长

$$\begin{gathered} 直角坐标：s={\int }_a^b\sqrt{1+[y^{\prime }(x){]}^2}dx \\ 参数方程：s={\int }_{\alpha }^{\beta }\sqrt{[x^{\prime }(t){]}^2+[y^{\prime }(t){]}^2}dt \\ 极坐标方程：s={\int }_{\alpha }^{\beta }\sqrt{[r(\theta ){]}^2+[r^{\prime }(\theta ){]}^2}d\theta \end{gathered}$$

3.旋转体体积

$$\begin{gathered} 绕x轴：V_x={\int }_a^b\pi y^2(x)dx \\ 绕y轴：V_y={\int }_a^{b}2\pi x|y(x)|dx(柱壳法) \\ 二重积分法：V=2\pi {\int }_a^{b}dx{\int }_{y_1(x)}^{y_2(x)}rdy(r为旋转半径) \end{gathered}$$

一定要理解，光背公式没用。另：推荐学习二重积分法求旋转体体积。

4.旋转曲面侧面积(x轴)

$$\begin{gathered} 直角坐标：S_x=2\pi {\int }_a^b|y(x)|\sqrt{1+[y^{\prime }(x){]}^2}dx \\ 参数方程：S_x=2\pi {\int }_{\alpha }^{\beta }|y(t)|\sqrt{[x^{\prime }(t){]}^2+[y^{\prime }(t){]}^2}dt \\ 极坐标：S_x=2\pi {\int }_{\alpha }^{\beta }r(\theta )\sin \theta \sqrt{[r(\theta ){]}^2+[r^{\prime }(\theta ){]}^2}d\theta \end{gathered}$$

5.形心：

$$\bar{x}=\frac{\iint xd\sigma }{\iint d\sigma }\bar{y}=\frac{\iint yd\sigma }{\iint d\sigma }$$

$$利用形心求特殊二重积分：\{\begin{array}{r}\iint xd\sigma =\bar{x}\cdot S_D\\ \iint yd\sigma =\bar{y}\cdot S_D\end{array}（其中D的形心(\bar{x},\bar{y})）$$

6.质心：

$$\begin{array}{rl}& ①\bar{x}=\frac{\int x\rho (x)dx}{\int \rho (x)dx}(\rho (x)为线密度)\\ & \\ & ②\bar{x}=\frac{\int x(t)ds}{\int ds}\bar{y}=\frac{\int y(t)ds}{\int ds}(参数方程，ds为弧微分)\end{array}$$

7.曲率和曲率半径：

$$\begin{array}{rl}& ①K=\frac{|y^{\prime \prime }|}{(1+y^{\prime 2}{)}^{\frac{3}{2}}}(K越大，R越小，弧度越小)\\ & ②R=\frac{1}{K}=\frac{(1+y^{\prime 2}{)}^{\frac{3}{2}}}{|y^{\prime \prime }|}\end{array}$$

    K[f1]大于K[f2]

8.平均值：

$$\bar{f}=\frac{1}{b-a}{\int }_a^{b}f(x)dx$$

8.反函数：

$$x_y^{\prime }=\frac{1}{y_x^{\prime }}{x}_{yy}^{\prime \prime }=-\frac{y_{xx}^{\prime \prime }}{{y_x^{\prime }}^3}$$

9.面积、体积相关：

$$S_{球}=4\pi R^2{V}_{球}=\frac{4}{3}\pi R^3$$

$$S_{椭圆}=\pi ab$$

10.点到线的距离公式：

$$D=\frac{|A{x}_0+B{y}_0+C|}{\sqrt{A^2+B^2}}$$

11.切线、法线、截距

$$\begin{array}{rl}& 设y=y(x)可导且y^{\prime }(x)\ne 0，则\\ ①& 切线方程：Y-y=y^{\prime }(x)(X-x)\\ & X=0时，y轴截距=y-x{y}^{\prime }(x)\\ & Y=0时，x轴截距=x-\frac{y}{y^{\prime }(x)}\\ ②& 法线方程：Y-y=-\frac{1}{y^{\prime }(x)}(X-x)\\ & X=0时，y轴截距=y+\frac{x}{y^{\prime }(x)}\\ & Y=0时，x轴截距=x+y{y}^{\prime }(x)\end{array}$$

十、复合函数

1.奇偶性：

$$对于f(g(x))：内偶则偶，内奇同外。$$

2.连续性：

$$\begin{gathered} \begin{array}{rl} \\ & 唯一确定的结论：\\ & 若g(x)在x_0处连续，f(u)在u_0=g(x_0)处连续，则f(g(x))在x_0处连续\end{array} \end{gathered}$$

十一、隐藏条件

    光滑曲线：处处连续且可导