【转】SPOJ 375 树链剖分

//SPOJ 375
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#define pb push_back
#define mp make_pair
#define eps 1e-9
#define zero(x) (fabs(x)<eps)
#define pi acos(-1.0)
#define f1 first
#define f2 second
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define initial 1,n,1
const int inf=0x3f3f3f3f;
const long long INF=1LL<<50;
using namespace std;
typedef long long LL;
typedef pair <int, int> PII;
template<typename X> inline bool minimize(X&p,X q){if(p<=q)return 0;p=q;return 1;}
template<typename X> inline bool maximize(X&p,X q){if(p>=q)return 0;p=q;return 1;}
#define N 10005
struct edge{
     int to,next;
}e[N<<1];
int head[N],fa[N],son[N],siz[N],dep[N];
int n,o,zzz;
int ww,w[N];
int tp[N];
int a[N][3];

void add(int x,int y)
{   e[o].to=y;
    e[o].next=head[x];
    head[x]=o++;
}

void dfs(int now)
{   son[now]=0; siz[now]=1;
    for (int i=head[now],v=e[i].to;~i;i=e[i].next,v=e[i].to)
        if (v!=fa[now])
        {   fa[v]=now; dep[v]=dep[now]+1;
            dfs(v);
            if (siz[v]>siz[son[now]]) son[now]=v;
            siz[now]+=siz[v];
        }
}
void maketree(int now,int top)
{   w[now]=++ww; tp[now]=top;
    if (son[now]!=0)    maketree(son[now],top);
    for (int i=head[now],v=e[i].to;~i;i=e[i].next,v=e[i].to)
    if (v!=fa[now]&&v!=son[now])
        maketree(v,v);
}

struct segtree{
    int tt[N<<2];
    void clear()
        {
            memset(tt,0,sizeof(tt));
        }
    void update(int pos,int l,int r,int rt)
        {
            if (pos==l&&pos==r) {tt[rt]=zzz;return;}
            int mid=(l+r)>>1;
            if (pos<=mid) update(pos,lson);
            if (mid<pos)  update(pos,rson);
            tt[rt]=max(tt[rt<<1],tt[rt<<1|1]);
        }
    int query(int L,int R,int l,int r,int rt)
         {   if (L<=l&&r<=R)  return tt[rt];
             int mid=(l+r)>>1;
             if (R<=mid) return query(L,R,lson);
             if (mid<L)  return query(L,R,rson);
             return max(query(L,R,lson),query(L,R,rson));
         }
}seg;
int find(int u,int v)
{   int f1=tp[u],f2=tp[v],re=0;
    while (f1!=f2)
        {   if (dep[f1]<dep[f2])
                {swap(f1,f2);swap(u,v);}
            re=max(re,seg.query(w[f1],w[u],initial));
            u=fa[f1]; f1=tp[u];
        }
    if (u==v) return re;
    if (dep[u]>dep[v]) swap(u,v);
    return max(re,seg.query(w[son[u]],w[v],initial));

}
char str[15];
void doit()
{
    scanf("%d",&n);
    memset(head,255,sizeof(head)); o=0;
    for (int i=1;i<n;i++)
        {
            scanf("%d%d%d",&a[i][0],&a[i][1],&a[i][2]);
            add(a[i][0],a[i][1]);
            add(a[i][1],a[i][0]);
        }
    siz[0]=0;
    int root=1;// all of [1,n] is ok
    memset(fa,0,sizeof(fa));
    dfs(root);
    ww=0; maketree(root,root);
    seg.clear();
//    for (int i=1;i<=n;i++)
//        printf("i=%d fa=%d son=%d tp=%d siz=%d w=%d\n",i,fa[i],son[i],tp[i],siz[i],w[i]);
    for (int i=1;i<n;i++)
        {
            if (dep[a[i][0]]>dep[a[i][1]]) swap(a[i][0],a[i][1]);
            zzz=a[i][2];
            seg.update(w[a[i][1]],initial);
        }
    scanf("%s",str); int x,y;
    while (str[0]!='D')
        {   scanf("%d%d",&x,&y);
            if (str[0]=='C')   {zzz=y;
                                seg.update(w[a[x][1]],initial);
                               }
            if (str[0]=='Q')  {printf("%d\n",find(x,y));}
            scanf("%s",str);
        }
}
int main()
{
    int cas;
    scanf("%d",&cas);
    while (cas--) doit();
}

树链，就是树上的路径。剖分，就是把路径分类为重链和轻链。
    记siz[v]表示以v为根的子树的节点数，dep[v]表示v的深度(根深度为1)，top[v]表示v所在的重链的顶端节点，fa[v]表示v的父亲，son[v]表示与v在同一重链上的v的儿子节点（姑且称为重儿子），w[v]表示v与其父亲节点的连边（姑且称为v的父边）在线段树中的位置。只要把这些东西求出来，就能用logn的时间完成原问题中的操作。


    重儿子：siz[u]为v的子节点中siz值最大的，那么u就是v的重儿子。
    轻儿子：v的其它子节点。
    重边：点v与其重儿子的连边。
    轻边：点v与其轻儿子的连边。
    重链：由重边连成的路径。
    轻链：轻边。


    剖分后的树有如下性质：
    性质1：如果(v,u)为轻边，则siz[u] * 2 < siz[v]；
    性质2：从根到某一点的路径上轻链、重链的个数都不大于logn。
   


    算法实现：
    我们可以用两个dfs来求出fa、dep、siz、son、top、w。
    dfs_1：把fa、dep、siz、son求出来，比较简单，略过。
    dfs_2：⒈对于v，当son[v]存在（即v不是叶子节点）时，显然有top[son[v]] = top[v]。线段树中，v的重边应当在v的父边的后面，记w[son[v]] = totw+1，totw表示最后加入的一条边在线段树中的位置。此时，为了使一条重链各边在线段树中连续分布，应当进行dfs_2(son[v])；
           ⒉对于v的各个轻儿子u，显然有top[u] = u，并且w[u] = totw+1，进行dfs_2过程。
           这就求出了top和w。
    将树中各边的权值在线段树中更新，建链和建线段树的过程就完成了。


    修改操作：例如将u到v的路径上每条边的权值都加上某值x。
    一般人需要先求LCA，然后慢慢修改u、v到公共祖先的边。而高手就不需要了。
    记f1 = top[u]，f2 = top[v]。
    当f1 <> f2时：不妨设dep[f1] >= dep[f2]，那么就更新u到f1的父边的权值(logn)，并使u = fa[f1]。
    当f1 = f2时：u与v在同一条重链上，若u与v不是同一点，就更新u到v路径上的边的权值(logn)，否则修改完成；
    重复上述过程，直到修改完成。


    求和、求极值操作：类似修改操作，但是不更新边权，而是对其求和、求极值。
    就这样，原问题就解决了。鉴于鄙人语言表达能力有限，咱画图来看看：树链剖分


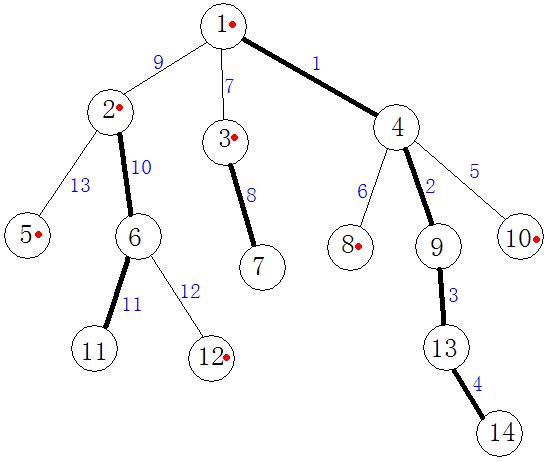
    如右图所示，较粗的为重边，较细的为轻边。节点编号旁边有个红色点的表明该节点是其所在链的顶端节点。边旁的蓝色数字表示该边在线段树中的位置。图中1-4-9-13-14为一条重链。


    当要修改11到10的路径时。
    第一次迭代：u = 11，v = 10，f1 = 2，f2 = 10。此时dep[f1] < dep[f2]，因此修改线段树中的5号点，v = 4, f2 = 1；
    第二次迭代：dep[f1] > dep[f2]，修改线段树中10--11号点。u = 2，f1 = 2；
    第三次迭代：dep[f1] > dep[f2]，修改线段树中9号点。u = 1，f1 = 1；
    第四次迭代：f1 = f2且u = v，修改结束。


**数据规模大时，递归可能会爆栈，而非递归dfs会很麻烦，所以可将两个dfs改为宽搜+循环。即先宽搜求出fa、dep，然后逆序循环求出siz、son，再顺序循环求出top和w。