【scoi 2011】糖果 差分约束

点击就送屠龙宝刀
简单的差分约束
其实差分约束这东西吧，日本白上讲的挺好的
就一句话
dis[from] + l[i].v <= dis[to]（最长路性质）
然后看到不等式什么的往上套就是了
如下图……（字不好，见谅）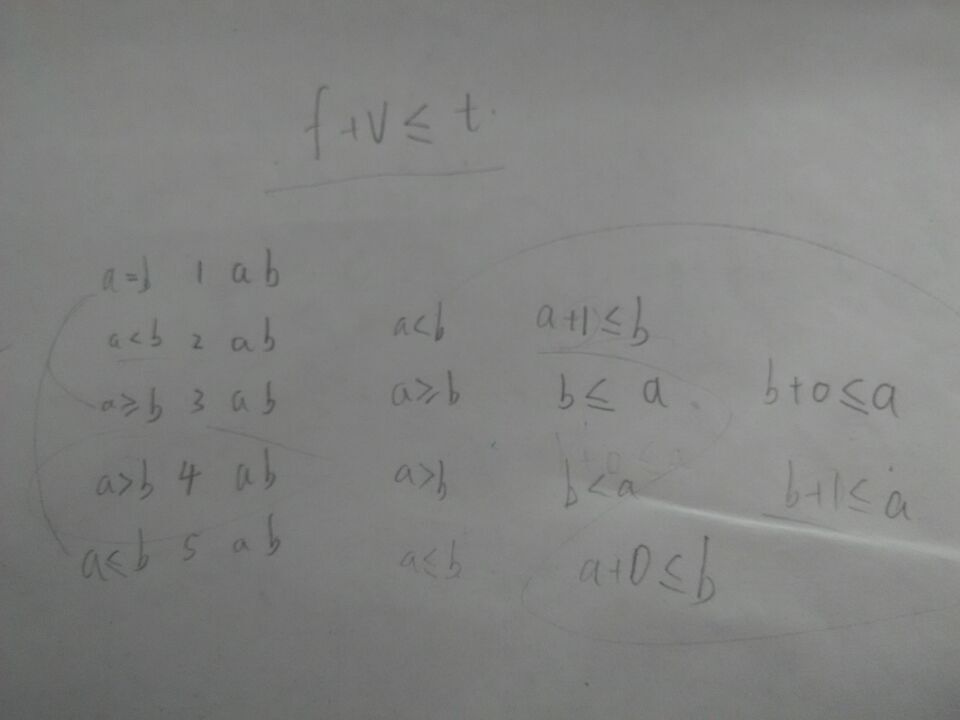

总之就是这样了
然后
差分约束的话不知道起点是谁
麻烦了
我的解决办法是建立超级源点（@网络流）
边权的话，保证不影响结果就是了
然后
跑什么路就看题了
他想最少就跑最长路，想最大就跑最短路

引用
比如给出三个不等式,b-a<=k1,c-b<=k2,c-a<=k3,求出c-a的最大值
由题b-a<=k1,c-b<=k2,得出c-a<=k1+k2,因此比较k1+k2和k3的大小，求出最小的就是c-a的最大值了

我习惯怎样都建正权
（负权好讨厌……）
还有啥来着……
差不多了吧
哦
对了
顺带一提
差分约束东西，边表示的是满足条件，也就是说边是条件……（好晕）
总之就是这样了
上代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const long long MAXN = 100000 + 5;
const long long MAXM = 200000 + 5;
struct edge
{
    long long f,t,v;
}l[MAXM << 1];
long long first[MAXN],next[MAXM << 1],tot;
void init()
{
    memset(first,0xfff,sizeof(first));
    tot = 0;
    return;
}
void build(long long f,long long t,long long v)
{
    l[++tot] = (edge){f,t,v};
    next[tot] = first[f];
    first[f] = tot;
    return;
}
long long dis[MAXN],use[MAXN];
long long vis[MAXN];
deque <int> q;
long long n;
long long spfa_slf(long long s)
{
    memset(dis,0x80,sizeof(dis));
    memset(use,0,sizeof(use));
    q.push_back(s);
    use[s] = true;
    dis[s] = 0;
    q.push_back(0);
    while(!q.empty())
    {
        long long u = q.front();
        q.pop_front();
        use[u] = false;
        if(vis[u] > n)
            return -1;
        for(long long i = first[u];i != -1;i = next[i])
        {
            long long v = l[i].t;
            if(dis[v] < dis[u] + l[i].v)
            {
                dis[v] = dis[u] + l[i].v;
                if(!use[v])
                {
                    vis[v] ++;
                    dis[v] > dis[q.front()] ? q.push_front(v) : q.push_back(v);
                }
            }
        }
    }
    long long ans = 0;
    for(long long i = 1;i <= n;i ++)
        ans += dis[i];
    ans += n;
    return ans;
}
long long k,x,a,b;
int main()
{
    init();
    scanf("%lld %lld",&n,&k);
    for(long long i = 1;i <= k;i ++)
    {
        scanf("%lld %lld %lld",&x,&a,&b);
        switch(x)
        {
            case 1:build(a,b,0);build(b,a,0);break;
            case 2:build(a,b,1);break;
            case 3:build(b,a,0);break;
            case 4:build(b,a,1);break;
            case 5:build(a,b,0);break;
        }
    }
    for(long long i = n;i >= 1;i --)
        build(n + 1,i,0);
    spfa_slf(0);
    printf("%lld\n",spfa_slf(n + 1));
    return 0;
}

转载于:https://my.oschina.net/u/2992707/blog/778008