不定人数的公平抽奖——蓄水池抽样思想

转自：https://huangjj27.gitlab.io/posts/fair-lottery/

仅做个人备份，浏览请看原文

 

题

已知有无法确定的总人数N(人数太多)参与抽奖，要从中随机抽取k个中奖者，要求保证每个中奖者的被抽中的概率为k/N

注意：本文所描述的公平是指每个人都以相同的概率被选中获奖

过程

1. 取出前k个参与者放到奖池中
2. 加入第n个参与者(k+1 <= n <= N)，进行如下的步骤：
   • 产生一个从1到n的随机数r
   • 如果r <= k，则将第n个参与者替换第r个参与者加入到奖池中，进入到下一轮
   • 如果r > k, 则不进行替换，直接进入下一轮。

数学证明

使用数学归纳法证明蓄水池抽样的算法的等概率性（公平性）

1. 初始化奖池后，只有k个元素加入抽奖，即n=k，前k个元素中奖的概率均为1=kk=kn1=kk=kn，等概率性成立。
2. 假设已经加入了n个(n≥kn≥k)元素，每个元素获奖(留在奖池里)的概率均为knkn
   则当加入第n+1个元素时，第n+1个元素被换入奖池的概率为kn+1kn+1
   对于前n个元素，有：

   留在奖池里的概率为 = 已经留在奖池的概率 * (第n+1个元素没有被换入奖池的概率 + 第n+1个元素换入奖池，替换奖池其他k-1个元素的概率)
   

   

   即当地n+1个元素加入后，加入的每个元素的概率均为kn+1kn+1， 等概率性成立。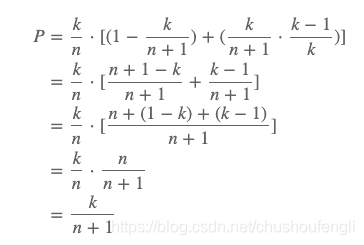
3. 综上，当N个元素均加入（被遍历）之后，每个元素留在奖池中的概率均相等，为kNkN

结论： 利用蓄水池抽样算法抽取的获奖结果是公平的。

实现

#############
# 暂时py实现 #
#############


# -*- coding: utf-8 -*-
import random
SAMPLE_COUNT = 10

# 默认使用系统时间作为种子，增加不可预测性
# 如果想要得到重复结果
# 可以使用固定的种子以选取固定的伪随机数数列
random.seed()
# random.seed(12345)

sample_titles = []
for index, line in enumerate(open("sample.txt")):
    # 初始化奖池
    if index < SAMPLE_COUNT:
        sample_titles.append(line)
    else:
        # 以递减的概率替换奖池里的元素
        # 选择从0到index的一个随机数
        r = random.randint(0, index)
        if r < SAMPLE_COUNT:
            sample_titles[r] = line

print sample_titles     # 打印中奖结果