AndroidX：新纪元的形状 (Shapes) ⭐

近期 Jetpack 全家桶推出了一个新的图形库：Graphics-Shapes (graphics:graphics-shapes:) 。本文在这里向大家介绍它是什么、怎么使用它，希望能够帮助到大家。

利用这个新的 graphics-shapes 库，我们能轻松创建和编辑复杂的圆角多边形。这个库主要有两个部分：形状 Shape 和形变 Morph。为了照顾注意力集中时间较短的读者，我打算分两篇文章来介绍这个库，第一篇介绍 Shape 部分，它允许我们轻松创建和渲染圆角多边形；第二篇则介绍如何为这些形状制作动画效果（又称作“Morph”）。

Android 提供了非常灵活的绘制 API。在自定义 View 时，我们可以重写 onDraw()，然后用参数 canvas 来绘制任何形状，从线条到圆形、矩形，再到复杂的 Path 对象。如果想画一些简单的圆角形状，我们可以利用 RoundRect()。

当然，你可以用 Path API 来实现任意复杂的圆角形状。但从开箱即用的角度来看，我们只有 Canvas.drawRoundRect() 这一个略显无力的 API，它的灵活性极小，矩形的每个圆角都是圆曲线，如果想要自定义圆角的形状或者顶点的数量，我们就得另想办法了。

终于， graphics-shapes 库诞生了，该库提供了一种简单的方式来创建各式各样的圆角形状，这也是我们创建这个库的初衷之一。

当设计师给出以上形状，要求开发人员在不给切图的情况下用代码画出来，他应该拉去枪毙 🔫。但一码归一码，如果我真能用代码实现出来，我应该获奖 🏅，对吧？

言归正传，我们希望创建出来的形状，不仅适用于未来的平台（Jetpack Compose），同时也能兼容旧的 Android View 系统，这样所有的开发者都能从中受益。所以我们在内部使用 Path 对象，Path 从 Android 1.0 开始就有了，这很 “AndroidX”（强兼容性），对吧？

用于创建和绘制这些形状的 API 其实并不难，复杂的实现细节都被隐藏起来了。开发者只需要理解两个部分：1.创建多边形；2.为形状提供可选的圆角参数。别担心，我会在下面介绍这些内容。

多边形

请允许我问你一个问题：什么是“多边形”？

你不必立马回答，可以试着从多个方面思考这个问题的答案。

我想我们有必要讨论一下“多边形”的含义。在我们使用 graphics-shapes 库的时候，这个术语代表什么，还是我们理解的传统意义上的多边形吗？

维基百科上对多边形的定义是这样的：

“多边形，是平面上封闭的几何图形，或者说是由 2 条以上在同一平面的线段首尾相连组成的形状。”

额，似乎不是很有帮助，数学家果然是数学家，明明写出来的是文字，听起来却像方程式。让我们为在座的各位简化这个定义。

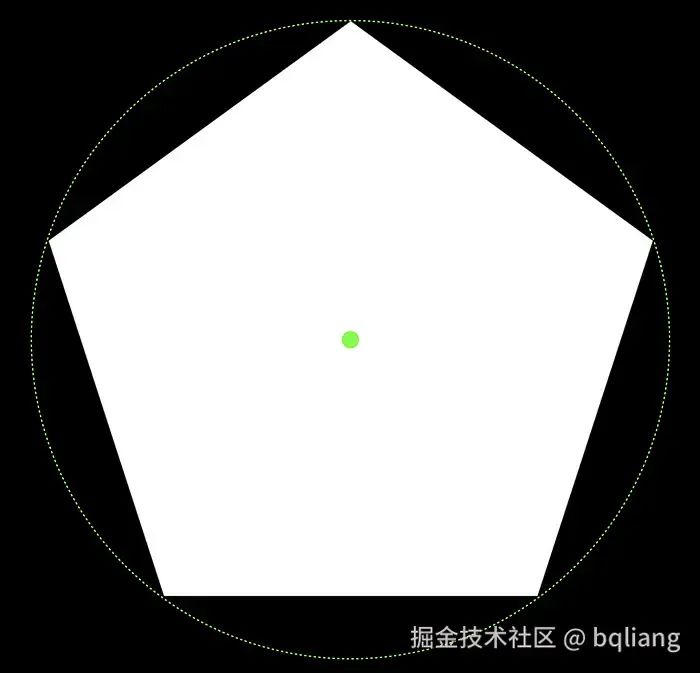
就其最基本的形式而言，多边形是具有边和顶点（或者“角”）的 2D 形状。人们对多边形的第一印象通常是：顶点围绕某个中心排列，所有边的长度都相等，比如下图的正五边形：

然而实际上，多边形可能比这复杂得多，包括可以自相交的形状，比如下图是一个具有自我相交边界的复杂五边形：

还好，我们库里面的“多边形”比较古板老套，它的顶点与某个中心等距，按顺序排列，所有的边都等长，也没有什么自相交（这个定义对处理形状之间的自动变形非常重要）。你可以将基本对象 RoundedPolygon 视为一个具有中心的形状，其所有顶点都围绕该中心，定位在距离中心给定半径处。

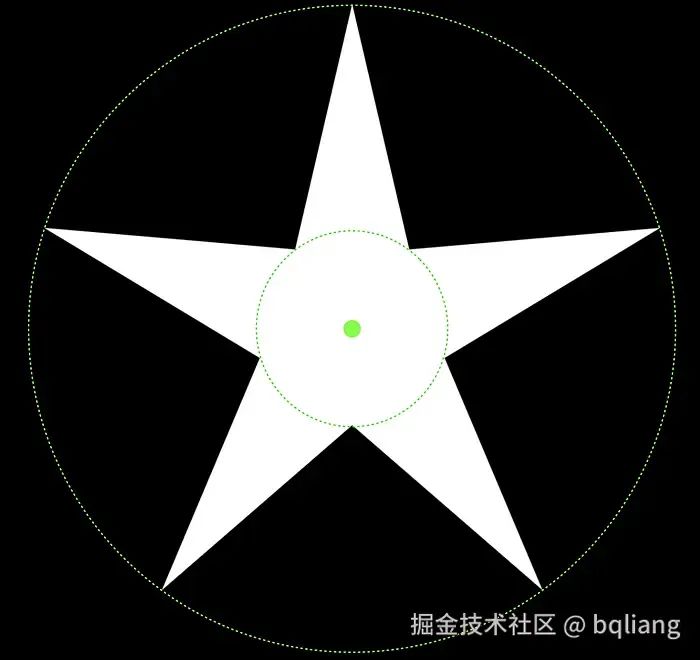
⭐ 我们的多边形也可以再稍微复杂一点， graphics-shapes 库里面有“星形多边形”的概念，星形多边形与多边形类似，只不过它具有内半径和外半径，顶点位于其中一个半径的圆轨迹之上

最后，我们的多边形具有“圆角”概念。严格来说，圆角不属于多边形概念的范畴，因为数学的多边形被定义为具有直边和尖角。因此，我们的形状命名为“圆角多边形（Rounded Polygons）”，该命名既体现了其作为多边形具有的一般概念，也体现了它带有可选圆角参数的额外差异。

圆角多边形具有和上述多边形类似的几何形状，不同之处在于每个顶点都有可选参数以描述如何将尖角圆化。例如下图是一个具有 5 条边的星形多边形，和上图类似，但外半径上的顶点所形成的角为圆角。

以上就是 graphics-shapes 库可以生成的所有类型的形状：非自相交的多边形，其顶点是有序的，与中心等距，且带有可选圆角。

对库的情况有了基本了解后，现在我们来看看如何使用 API 来创建这些形状。

多边形、星形......

用于创建形状的主要类是 RoundedPolygon，你可以用这个 API 创建出许多不同的形状，但它们都归结为多边形的变体。

要创建简单的非圆角的五角星形状，只要告诉 RoundedPolygon 你想要多少个顶点，并提供可选的半径和中心点。当然任何形状都会有半径和中心，只是默认情况下，库会以 (0, 0) 为中心，1 为半径创建形状。你可以通过变换（缩放、平移、旋转）形状，使其达到所需的大小和位置：RoundedPolygon.transform(Matrix)。

题外话，不知道你会不会产生疑问，为什么一个命名为 Rounded... 的 API 可以创建出来一个非圆角的东西？好吧，其实最初为了处理这种语义上的差异，我们有父类 Polygon 和子类 RoundedPolygon，但最终我们还是觉得，仅仅因为学术上的“多边形”不带圆角，就要用两个类来分割功能，这属实没必要，因此我们决定用一个类来处理所有情况。

"API 命名是困难的、不完美的，也是永远令人遗憾的根源。"

总之，API 最简单的使用方法就是传入顶点的数量，让库来完成生成形状的工作，随后可以调用 transform() 函数来调整对象的大小和位置，最后将形状写入 Path 对象中将其绘制到你的 View 中。

下面是一个简单示例，创建了一个半径为 300 像素的五边形，将生成的形状写入 Path 后，再用 Canvas 画出来。

class Pentagon(...) : View(...) {
    private val paint = /* ... */
    private val path = Path()

    override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        val pentagon = RoundedPolygon(
            numVertices = 5,
            radius = 300f,
            centerX = (w / 2).toFloat(),
            centerY = (h / 2).toFloat()
        )
        pentagon.toPath(path)
    }

    override fun onDraw(canvas: Canvas) {
        canvas.drawPath(path, paint)
    }
}

星形多边形也很简单，但稍微特殊一点，我们要用 RoundedPolygon 类的静态方法 star() 来创建它。可以通过可选参数 innerRadius 指定内半径（默认值为 0.5）。

val pentagonalStar = RoundedPolygon.star(
 numVerticesPerRadius = 5,
    innerRadius = 180f,
    radius = 300f
)

Rounding Error

我们创建了一个简单的 API 来创建和绘制正多边形和星形多边形，但即使没有 graphics-shapes 库，用现有的 API 来创建这种的直边、尖角的形状好像也不是什么难事，有趣且棘手的部分是如何将这些角圆化。

为了弄清楚这个问题，（就我而言）我重新学习了一大堆高中数学知识，包括几何学和三角学，诸如三角恒等式、余弦定理，以及像三角形的内角和为 180 度这样的几何知识都派上了用场。也许在未来我会抽时间写一下它们都被用在哪里，如果你感兴趣的话也可以翻翻代码。

对于库的使用者来说，关键在于如何使用 API 创建出让人心甘情愿花费 200 万的圆角形状。

别担心，API 比实现细节简单得多，创建具有圆角的多边形或星形多边形，只不是在调用上述 API 的基础之上，再额外提供有关圆角的附加信息而已。

要完成这项任务，请使用 CornerRounding 类，它负责确定如何圆化尖角。创建该类的实例需要提供两个参数：radius 和 smoothing。

半径

radius 是用于圆化顶点的圆的半径。这个参数的作用类似于 Canvas.drawRoundRect() 方法的参数 radius，只不过它和可选参数 smoothing（详见下文）共同决定圆角的效果。例如，我们可以创建这样一个圆角正三角形：

其中每个角的圆角半径 r 用几何方式表示如下：

半径 r 决定了圆角的尺寸。请注意，圆角半径会在顶点相交的两条直边之间的拐角处产生纯圆曲线（红色部分）。

平滑拐角

和半径 radius 不同，在我们的库中 smoothing 是一个新概念。你可以将 smoothing 视为一个平滑因子，它决定了从圆角部分过渡到直边的平滑程度。

平滑因子为 0（非平滑，CornerRounding 的默认值）时，会得到纯粹的圆角（当然前提是非零半径），换句话说，此时的圆角部分就只是一条纯圆曲线。
非零平滑因子（最大值为 1.0）会导致圆角部分由三条独立的曲线共同组成，其中中间部分是由圆角半径生成的圆弧，也就是前面谈到的那条纯圆曲线，但这条纯圆曲线不再直接延申到多边形的直边，而是通过两条“侧翼”曲线从圆弧平滑过渡到直边，这些侧翼曲线自身是平滑（非圆形）的弧。

平滑曲线的程度决定了中间圆弧的长度（平滑度越大 ==> 圆弧越短）和侧翼曲线的长度（平滑度越大 ==> 侧翼曲线越长）。

侧翼曲线不仅影响圆角中纯圆弧部分的比例，还会影响整体圆角的长度，较大的平滑因子会将圆角与直边的的交点沿边缘推向下一个顶点。平滑因子达到 1（最大值）时，中间纯圆弧的长度为零，此时侧翼曲线的长度达到最大（最长时甚至可以延伸到下一个顶点）。

请注意，所有多边形在内部都由贝塞尔三次曲线列表表示，每条曲线由一对锚点和一对控制点定义。这些三次曲线主要用于在内部创建 Path 对象，以便稍后我们能将形状绘制到自定义 View 中。

注意：三次平面曲线的相关内容已经一定程度上脱离了本文的中心，我不想在这里过多解释它，网络上有很多关于贝塞尔曲线、三次曲线、路径等资料可以查阅。如果你对这些概念不熟悉，我建议你先花一点时间进行学习。这里有一个非常简单的描述，希望对你有所帮助：一条三次贝塞尔曲线可以由两个锚点（曲线的两端）和两个控制点来定义，这两个控制点能够确定锚点处曲线的斜率。

译者（bqliang）曾写过一篇《Android 动画里的贝塞尔曲线》，相信对大家快速理解三次曲线会有一定的帮助。

在这里我想特别推荐一下这个贝塞尔曲线入门网站。这是一个关于贝塞尔曲线的巨大知识宝库，里面有各种证明、方程、示例代码、图表、嵌入式实时演示和详细解释。我经常打开这个网站，以进一步理解这个复杂而有趣的领域。

文字太枯燥了，让我们来看一些稍微直观点的图片吧。

形状的角（左侧的白色填充对象）在右侧用绿色线条（形状的轮廓）和白色虚线（给定圆角半径的圆）表示。
三次曲线由粉色圆圈（锚点）、黄色圆圈（曲线的控制点）、锚点与控制点之间的黄线表示。如果你有使用过像 Adobe Illustrator、Photoshop 等绘图程序，在绘制曲线时可能见过类似的控制手柄。

平滑因子为 0（非平滑）时，会产生一条三次曲线，该曲线与拐角处具有指定圆角半径的纯圆弧重合。

当我们提供非零平滑因子时，圆角由 3 条三次曲线共同组成：圆形三次曲线（与上面的非平滑情况下看到的一样）加上两条在圆形曲线和直边之间过渡的侧翼曲线。注意，与非平滑的情况相比较，侧翼曲线在直边上的起始点更靠后。平滑的效果可能非常微妙，但它们为设计人员提供了更大的灵活性，可以生成超越传统圆角的平滑形状。

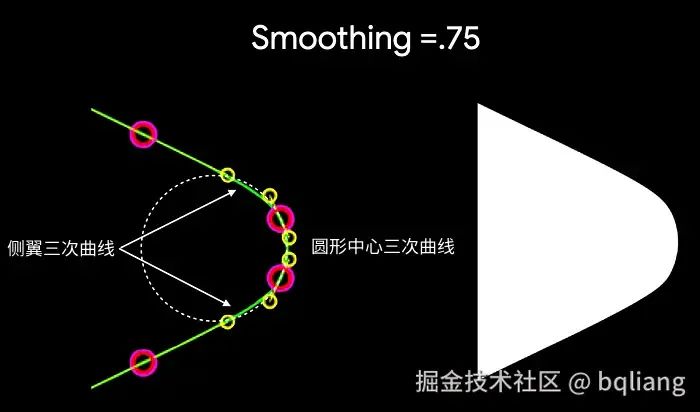
呃，也许我应该提一下，3 条独立线段连接起来的曲线，竟然比一条纯圆曲线还要平滑，听上去好像不那么真实，但事实确实如此，不信你问原研哉

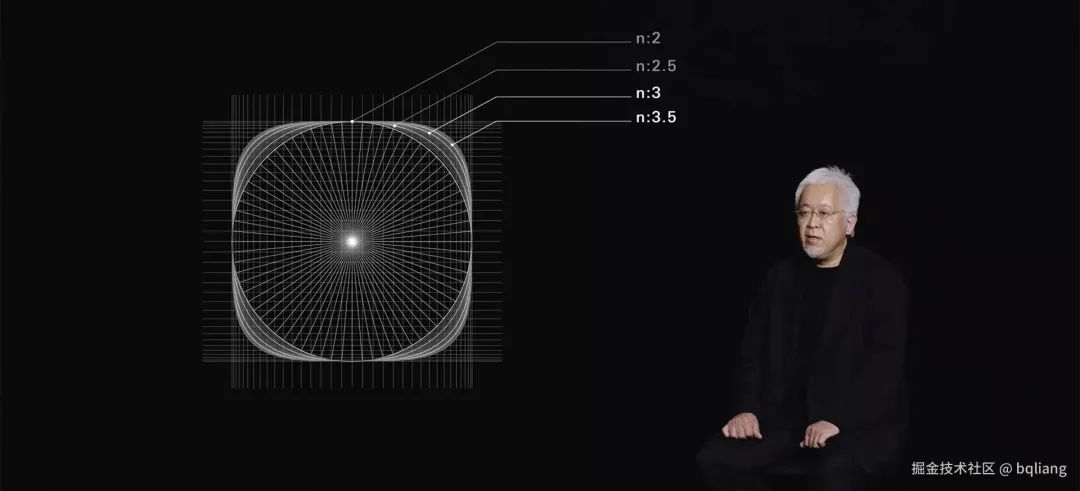
开玩笑开玩笑，由 3 条独立线段构成的圆角看起来如此丝滑的真正原因是，每条曲线都经过计算，以匹配与下一个连接点的斜率。例如，圆角会从纯圆弧曲线平滑过渡到非圆形的平滑侧翼曲线，然后再次过渡到直边。

呼，真是一场酣畅淋漓的... 数学之旅？无论如何，总算是把 CornerRounding 类的两个参数讲完了。

One More Thing

除了上面介绍的采用顶点数量的构造函数之外，还有一个更通用的构造函数，它采用顶点列表：

fun RoundedPolygon(
    vertices: FloatArray, // 📌
    rounding: CornerRounding = CornerRounding.Unrounded,
    perVertexRounding: List<CornerRounding>? = null,
    centerX: Float = Float.MIN_VALUE,
    centerY: Float = Float.MIN_VALUE
)

FloatArray 中必须传入至少 3 个顶点的坐标，也就是说数组长度不能小于 6。

这个构造函数让您可以创建一些形状……这些形状可能不太符合我们对圆角多边形的假设。因此，如果您传入随机复杂的顶点列表，结果可能不如其他构造函数生成的更受约束的多边形那样令人满意，也不要感到惊讶。

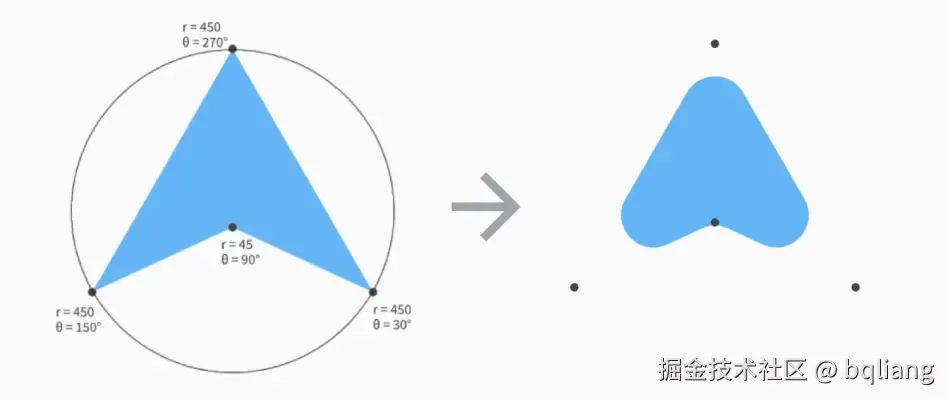
这个构造函数存在的意义是为了创建一些更有趣的多边形形状，这些形状的顶点与中心点的距离可能并不相等。例如，我们可以使用顶点列表构造函数来创建一个底边内凹的三角形形状：

这个形状的大部分是……但不完全是正三角形。所以需要使用顶点列表版本的构造函数来创建底部边缘“凹”的形状，它的代码如下：

class CustomTriangleShape(context: Context) : View(context){
    private lateinit var PointCenter : PointF
    private val paint = /* ... */
    private val path = Path()

    override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        PointCenter = PointF((w/2).toFloat(), (h/2).toFloat())

        val triangleInnerRadiusRatio = 38f
        val trianglePoints = listOf(
            radialToCartesian(380f, 270f.toRadians()),
            radialToCartesian(380f, 30f.toRadians()),
            radialToCartesian(triangleInnerRadiusRatio, 90f.toRadians()),
            radialToCartesian(380f, 150f.toRadians()),
        ).flatMap { listOf(it.x, it.y) }.toFloatArray()
        val triangle = RoundedPolygon(trianglePoints, CornerRounding(66f))
        triangle.toPath(path)
    }

    override fun onDraw(canvas: Canvas) {
        canvas.drawPath(path, paint)
    }

    // 角度转弧度
    private fun Float.toRadians(): Float = this * PI.toFloat() / 180f

    //根据给定的弧度角，计算在二维平面上对应的单位方向向量（单位向量长度为1）
    private fun directionVectorPointF(angleRadians: Float): PointF =
        PointF(cos(angleRadians), sin(angleRadians))

    // 极坐标转笛卡尔坐标
    private fun radialToCartesian(
        radius: Float, // 极径
        angleRadians: Float, // 极度
        center: PointF = PointCenter // 极点
    ): PointF = directionVectorPointF(angleRadians) * radius + center
}

如果看得有点吃力，建议先学习一下极坐标和笛卡尔坐标相关知识

前面我一直在具体讨论单一的 CornerRounding 参数的情况，但指定多个（内半径和外半径）圆角参数也是可以的，这样我们就能在星形多边形上实现类似的效果。

内部顶点可以使用与外部顶点不同的圆角参数，图中的外部顶点是非纯圆角的。

fun RoundedPolygon.Companion.star(
    numVerticesPerRadius: Int,
    radius: Float = 1f,
    innerRadius: Float = .5f,
    rounding: CornerRounding = CornerRounding.Unrounded, // 📌
    innerRounding: CornerRounding? = null, // 📌
    perVertexRounding: List<CornerRounding>? = null,
    centerX: Float = 0f,
    centerY: Float = 0f
): RoundedPolygon

只要你想，还可以为每个顶点定义不同圆角参数，从而创造更个性化的形状。

各种各样千奇百怪的圆角（或非圆角）多边形形状，你都可以借助这个库将它绘制出来。当然，你一直都可以在 Android 上实现这些功能，毕竟我们也只是使用了底层的 Path API 来处理绘图过程，只是在这个过程中有很多细节（以及大量数学计算）需要解决，我们希望这个新库能让这项工作变得更加容易。