字典序法生成全排列算法的证明

引言

对一个给定数据进行全排列，在各种场合经常会用到。组合数学中，生成全排列的方法有很多，卢开澄老师的《组合数学》中就介绍了三种：序数法，字典序法，临位互换法等。其中以字典序法由于算法简单，并且使用的时候可以依照当前状态获取下一个状态，直到所有排列全部完成，方便在程序中随要随用，应用比较广泛，STL中的Next_permutation也是使用此法。

算法定义

首先看什么叫字典序，顾名思义就是按照字典的顺序（a-z, 1-9）。以字典序为基础，我们可以得出任意两个数字串的大小。比如 "1" < "12"<"13"。 就是按每个数字位逐个比较的结果。对于一个数字串，“123456789”， 可以知道最小的串是 从小到大的有序串“123456789”，而最大的串是从大到小的有序串“*987654321”。这样对于“123456789”的所有排列，将他们排序，即可以得到按照字典序排序的所有排列的有序集合。

如此，当我们知道当前的排列时，要获取下一个排列时，就可以范围有序集合中的下一个数（恰好比他大的）。比如，当前的排列时“123456879”， 那么恰好比他大的下一个排列就是“123456897”。 当当前的排列时最大的时候，说明所有的排列都找完了。

于是可以有下面计算下一个排列的算法：

设P是1～n的一个全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn

　　1）从排列的右端开始，找出第一个比右边数字小的数字的序号j（j从左端开始计算），即 j=max{i|pi<pi+1}

　　2）在pj的右边的数字中，找出所有比pj大的数中最小的数字pk，即 k=max{i|pi>pj}（右边的数从右至左是递增的，因此k是所有大于pj的数字中序号最大者）

　　3）对换pj，pk

　　4）再将pj+1......pk-1pkpk+1......pn倒转得到排列p'=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1，这就是排列p的下一个排列。

证明

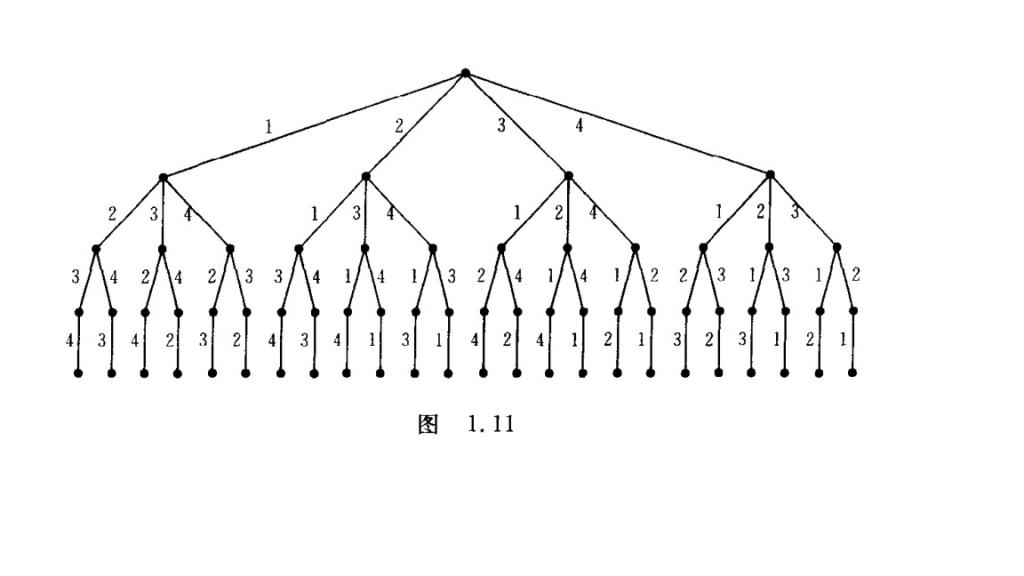
要证明这个算法的正确性，我们只要证明生成的下一个排序是恰好比当前排列大的一个序列即可。图1.11是从卢开澄老师的《组合数学》中截取的一个有1234生成所有排序的字典序树。从左到右的每一个根到叶子几点的路径就是一个排列。下面我们将以这个图为基础，来证明上面算法的正确性。

算法步骤1，得到的子串 s = {pj+1,.....,pn}， 是按照从大到小进行排列的。即有 pj+1 > pj+2 > ... > pn， 因为 j=max{i|pi<pi+1}。

算法步骤2，得到了最小的比pj大的pk，从n往j数，第一个比j大的数字。将pk和pj替换，保证了替换后的数字比当前的数字要大。

于是得到的序列为p1p2...pj-1pkpj+1...pk-1pjpk-1...pn.注意这里已经将pk替换成了pk。

这时候我们注意到比p1..pj-1pk.....，恰好比p1....pj.....pn大的数字集合。我们在这个集合中挑选出最小的一个即时所要求的下一个排列。

算法步骤3，即是将pk后面的数字逆转一下（从从大到小，变成了从小到大。）

由此经过上面3个步骤得到的下个排列时恰好比当前排列大的排列。

同时我们注意到，当所有排列都找完时，此时数字串从大到小排列。步骤1得到的j = 0，算法结束。

算法实现

[java]  view plain copy print ?

1. /** 
2.  * get the next permutation based on dictionary order method 
3.  *  
4.  * @param cur 
5.  * @return next permutation string, or null if cur is the last 
6.  */  
7. public static String next(String cur) {  
8.     String ret = null;  
9.     if (cur == null)  
10.         return ret;  
11.     int strlen = cur.length();  
12.     char[] lcur = cur.toLowerCase().toCharArray();  
13.     int j = strlen - 2;  
14.     while (j >= 0 && lcur[j] > lcur[j + 1]) {  
15.         j--;  
16.     }  
17.     if (j < 0)  
18.         return ret;  
19.   
20.     int k = strlen - 1;  
21.     while (lcur[k] < lcur[j]) {  
22.         k--;  
23.     }  
24.   
25.     // swap lcur[k], lcur[j]  
26.     char temp = lcur[k];  
27.     lcur[k] = lcur[j];  
28.     lcur[j] = temp;  
29.   
30.     // reverse lcur[j+1, ..., strlen-1]  
31.     int low = j + 1;  
32.     int high = strlen - 1;  
33.     while (low < high) {  
34.         temp = lcur[low];  
35.         lcur[low] = lcur[high];  
36.         lcur[high] = temp;  
37.         low++;  
38.         high--;  
39.     }  
40.     ret = String.valueOf(lcur);  
41.     return ret;  
42. }