Python sklearn数据分析中常用方法

最新推荐文章于 2024-10-12 12:55:48 发布

cooledi

最新推荐文章于 2024-10-12 12:55:48 发布

阅读量1.6k

点赞数

分类专栏： python

python 专栏收录该内容

4 篇文章 0 订阅

订阅专栏

一、数据处理

随机划分训练集和测试集：

1使用train_test_split

from sklearn.model_selection import train_test_split

X_all = data_train.drop(['Survived', 'PassengerId'], axis=1) #只包含特征集，不包含预测目标
y_all = data_train['Survived'] #只包含预测目标

num_test = 0.20 # 测试集占据比例，，如果是整数的话就是样本的数量
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, test_size=num_test, random_state=23)
# random_state参数表示随机种子，如果为0或不填，每次随机产生的随机数组不同。

2 使用交叉验证(Cross-validation)

参考：莫烦的视频 https://www.bilibili.com/video/av17003173/index_8.html#page=10

3 使用StratifiedShuffleSplit

from  sklearn.model_selection import StratifiedShuffleSplit
StratifiedShuffleSplit(n_splits=10,test_size=None,train_size=None, random_state=None)

3.1 参数说明

参数 n_splits是将训练数据分成train/test对的组数，可根据需要进行设置，默认为10
参数test_size和train_size是用来设置train/test对中train和test所占的比例。例如：
1.提供10个数据num进行训练和测试集划分
2.设置train_size=0.8 test_size=0.2
3.train_num=num*train_size=8 test_num=num*test_size=2
4.即10个数据，进行划分以后8个是训练数据，2个是测试数据

注*：train_num≥2，test_num≥2 ;test_size+train_size可以小于1*

参数 random_state控制是将样本随机打乱

3.2 函数作用描述
a.其产生指定数量的独立的train/test数据集划分数据集划分成n组。
b.首先将样本随机打乱，然后根据设置参数划分出train/test对。

c.其创建的每一组划分将保证每组类比比例相同。即第一组训练数据类别比例为2:1，则后面每组类别都满足这个比例

3.3 具体实现

from sklearn.model_selection import StratifiedShuffleSplit
import numpy as np
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4],
              [1, 2],[3, 4], [1, 2], [3, 4]])#训练数据集8*2
y = np.array([0, 0, 1, 1,0,0,1,1])#类别数据集8*1

ss=StratifiedShuffleSplit(n_splits=5,test_size=0.25,train_size=0.75,random_state=0)#分成5组，测试比例为0.25，训练比例是0.75

for train_index, test_index in ss.split(X, y):
   print("TRAIN:", train_index, "TEST:", test_index)#获得索引值
   X_train, X_test = X[train_index], X[test_index]#训练集对应的值
   y_train, y_test = y[train_index], y[test_index]#类别集对应的值

运行结果：

从结果看出，1.训练集是6个，测试集是2，与设置的所对应；2.五组中每组对应的类别比例相同

二、模型选择

以下是最常用的机器学习算法，大部分数据问题都可以通过它们解决：

1.线性回归 (Linear Regression)

2.逻辑回归 (Logistic Regression)

3.决策树 (Decision Tree)

4.支持向量机（SVM）

5.朴素贝叶斯 (Naive Bayes)

6.K邻近算法（KNN）

7.K-均值算法（K-means）

8.随机森林 (Random Forest)

9.降低维度算法（Dimensionality Reduction Algorithms）

10.Gradient Boost和Adaboost算法

1.线性回归 (Linear Regression)

线性回归是利用连续性变量来估计实际数值（例如房价，呼叫次数和总销售额等）。我们通过线性回归算法找出自变量和因变量间的最佳线性关系，图形上可以确定一条最佳直线。这条最佳直线就是回归线。这个回归关系可以用Y=aX+b 表示。

我们可以假想一个场景来理解线性回归。比如你让一个五年级的孩子在不问同学具体体重多少的情况下，把班上的同学按照体重从轻到重排队。这个孩子会怎么做呢？他有可能会通过观察大家的身高和体格来排队。这就是线性回归！这个孩子其实是认为身高和体格与人的体重有某种相关。而这个关系就像是前一段的Y和X的关系。

在Y=aX+b这个公式里：

Y- 因变量

a- 斜率

X- 自变量

b- 截距

a和b可以通过最小化因变量误差的平方和得到（最小二乘法）。

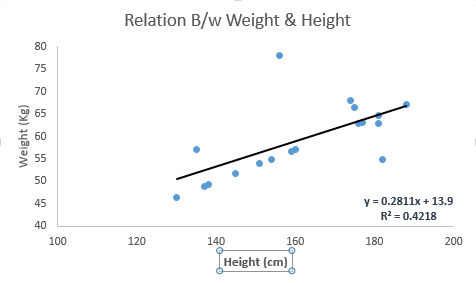
下图中我们得到的线性回归方程是 y=0.2811X+13.9。通过这个方程，我们可以根据一个人的身高得到他的体重信息。

线性回归主要有两种：一元线性回归和多元线性回归。一元线性回归只有一个自变量，而多元线性回归有多个自变量。拟合多元线性回归的时候，可以利用多项式回归（Polynomial Regression）或曲线回归 (Curvilinear Regression)。

#Import Library
#Import other necessary libraries like pandas, numpy...
from sklearn import linear_model
#Load Train and Test datasets
#Identify feature and response variable(s) and values must be numeric and numpy arrays

x_train=input_variables_values_training_datasets
y_train=target_variables_values_training_datasets
x_test=input_variables_values_test_datasets

# Create linear regression object
linear = linear_model.LinearRegression()

# Train the model using the training sets and check score
linear.fit(x_train, y_train)
linear.score(x_train, y_train)

#Equation coefficient and Intercept
print('Coefficient: \n', linear.coef_)
print('Intercept: \n', linear.intercept_)

#Predict Output
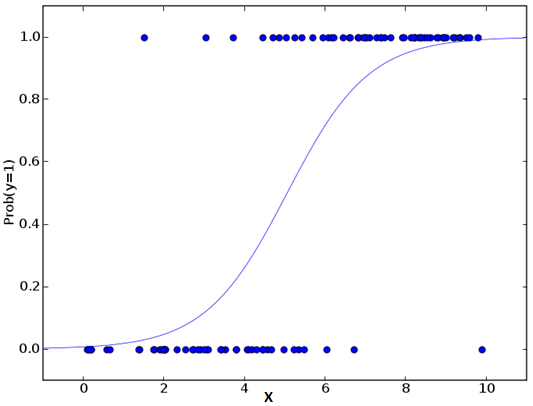
predicted= linear.predict(x_test)

2.逻辑回归

别被它的名字迷惑了，逻辑回归其实是一个分类算法而不是回归算法。通常是利用已知的自变量来预测一个离散型因变量的值（像二进制值0/1，是/否，真/假）。简单来说，它就是通过拟合一个逻辑函数（logit fuction）来预测一个事件发生的概率。所以它预测的是一个概率值，自然，它的输出值应该在0到1之间。

同样，我们可以用一个例子来理解这个算法。

假设你的一个朋友让你回答一道题。可能的结果只有两种：你答对了或没有答对。为了研究你最擅长的题目领域，你做了各种领域的题目。那么这个研究的结果可能是这样的：如果是一道十年级的三角函数题，你有70%的可能性能解出它。但如果是一道五年级的历史题，你会的概率可能只有30%。逻辑回归就是给你这样的概率结果。

回到数学上，事件结果的胜算对数（log odds）可以用预测变量的线性组合来描述：

odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence

ln(odds) = ln(p/(1-p))

logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk

在这里，p 是我们感兴趣的事件出现的概率。它通过筛选出特定参数值使得观察到的样本值出现的概率最大化，来估计参数，而不是像普通回归那样最小化误差的平方和。

你可能会问为什么需要做对数呢？简单来说这是重复阶梯函数的最佳方法。

延伸：

以下是一些可以尝试的优化模型的方法：

加入交互项（interaction）
减少特征变量
正则化（regularization）
使用非线性模型

3.决策树

这是我最喜欢也是能经常使用到的算法。它属于监督式学习，常用来解决分类问题。令人惊讶的是，它既可以运用于类别变量（categorical variables）也可以作用于连续变量。这个算法可以让我们把一个总体分为两个或多个群组。分组根据能够区分总体的最重要的特征变量/自变量进行。更详细的内容可以阅读这篇文章Decision Tree Simplified。

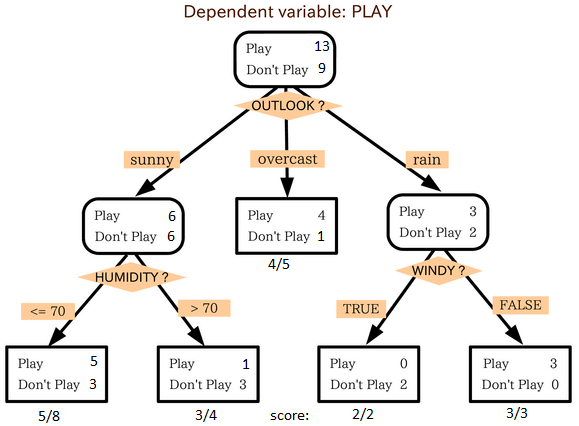
从上图中我们可以看出，总体人群最终在玩与否的事件上被分成了四个群组。而分组是依据一些特征变量实现的。用来分组的具体指标有很多，比如Gini，information Gain, Chi-square,entropy。

理解决策树原理的最好的办法就是玩Jezzball游戏。这是微软的一款经典游戏（见下图）。这个游戏的最终任务是在一个有移动墙壁的房间里，通过建造墙壁来尽可能地将房间分成尽量大的，没有小球的空间。

每一次你用建墙来分割房间，其实就是在将一个总体分成两部分。决策树也是用类似方法将总体分成尽量多的不同组别。

#Import Library
#Import other necessary libraries like pandas, numpy...

from sklearn import tree
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

# Create tree object 
model = tree.DecisionTreeClassifier(criterion='gini') # for classification, here you can change the algorithm as gini or entropy (information gain) by default it is gini  

# model = tree.DecisionTreeRegressor() for regression

# Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)

#Predict Output
predicted= model.predict(x_test)

参考与：http://blog.csdn.net/han_xiaoyang/article/details/51191386

http://blog.csdn.net/qq_16234613/article/details/76534673