c#扩展方法奇思妙用变态篇一：由Fibonacci数列引出“委托扩展”及“递推递归委托”...

先回顾一个数列的概念：按一定次序排列的一列 数 称为数列...(请参见百度百科：数列)
几个简单的数列：
      1, 1, 1, 1, 1, 1, 1...                //数列1
      0, 1, 2, 3, 4, 5, 6, 7...                //数列2
      0, 1, 4, 9, 16, 25, 36, 49...        //数列3
通项公式的定义：数列的第n项与项的序数这间的关系，也就是数列生成算法
上面几个数列可表示为
       An = F(n) = 1
       An = F(n) = n
       An = F(n) = n * n

有了数列和通项公式的定义，我们的任务就好描述了：
      用最简洁的代码描述通项公式，用最简洁算法生成数列的前N个数。

在此要求下，用常规代码是做不到简洁的，这里我们用lambda表达式描述通项公式：

         // 数列1 通项公式
         public   static  Func < int ,  int >  fun1  =  n  =>   1 ;
         // 数列2 通项公式
         public   static  Func < int ,  int >  fun2  =  n  =>  n;
         // 数列3 通项公式
         public   static  Func < int ,  int >  fun3  =  n  =>  n  *  n;

 

lambda表达式是不是与数学公式很像啊！

再来看生成算法，这里用了一个不一般的扩展：

         /// 
        /// 生成队列的前count项
        /// 
        /// 通项公式
        /// 生成的数量
        /// 队列前count项
         public   static  IEnumerable < int >  GetSequence( this  Func < int ,  int >  func,  int  count)
         {
            for (int i = 0; i < count; i++) yield return func(i);
        }

相信大家见的扩展大多针对类(object, string)、接口(IEnumerable)进行扩展，针对Func（委托）估计对大多数人来说都是第一次。
这个扩展就是标题中说的“委托扩展”，感觉很怪吧，很别扭吧，很别管太多，看看怎么调用吧：

         public   static   void  Test1()
        {
             int [] ints1  =  fun1.GetSequence( 10 ).ToArray();       // 1, 1, 1, 1
             int [] ints2  =  fun2.GetSequence( 10 ).ToArray();       // 0, 1, 2, 3
             int [] ints3  =  fun3.GetSequence( 10 ).ToArray(); ;     // 0, 1, 4, 9
        }

自我感觉比较简洁，而且将生成数列（GetSequence）与数列算法(通项公式)分开，也达到了生成数列（GetSequence）的复用。

上面几个数列比较简单，现在来看Fibonacci，
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
用图形表示如下：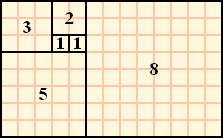

这个序列在大家学习c语言递推递归时都接触过，这个序列很神奇，请参看维基百科：斐波那契数列
它的通项公式是 An = F(n) = n                          n =0, 1
                                       F(n-1) + F(n-2)      n>1
注意：关于这数列有的是从n从0开始，有的是从1开始，这里不计较。

递推递归算法如下，容易理解效率确很低！！

         public   static   int  GetFibonacci( int  n)
        {
             if  (n  >   1 )  return  GetFibonacci(n  -   1 )  +  GetFibonacci(n  -   2 );
             else   return  n;
        }

本文是为了引出递推递归委托，暂不是算法的效率
下面就要大（改）变（形）态了。

不考虑 <1 的情况

         public   static  Func < int ,  int >  Fibonacci  =  n  =>  Fibonacci(n  -   1 )  +  Fibonacci(n  -   2 );

与数学通项式对比一下，何其相似！这就是我们的“递推递归委托”！

考虑所有情况，完成Fibonacci，如下

         public   static  Func < int ,  int >  Fibonacci  =  n  =>  n  >   1   ?  Fibonacci(n  -   1 )  +  Fibonacci(n  -   2 ) : n;

实在感叹c#精简的语法，一句代码可以表示一个递推递归！
调用测试下吧！

         public   static   void  Test2()
        {  
             // 委托扩展方法 + 递推递归委托
             int [] fibonacciSequence  =  Fibonacci.GetSequence( 12 ).ToArray();
        }

当然这个生成算法效率不是一般的低！

最后给出一个数学推导出的精确算法

         public   static  Func < int ,  int >  Fibonacci2  =  n  =>  ( int )( 5.0 .Pow( - 0.5 )  *  (( 0.5   *  ( 1   +   5.0 .Pow( 0.5 ))).Pow(n  +   1 )  -  ( 0.5   *  ( 1   -   5.0 .Pow( 0.5 ))).Pow(n  +   1 )));
         // Pow扩展，简化调用
         public   static   double  Pow( this   double  x,  double  y)
        {
             return  Math.Pow(x, y);
        }

一点意见：像这样代码，最好是给封装起来，否则会很麻烦的。
这篇文章是给极少数人看的（启发一下），看完后封装好给大多数人用。这是也“变态篇”系列文章的宗旨.
希望大家对 “委托扩展” 和 “递推递归委托”提些看法，名字定义不太好，请指正！

来自 “ ITPUB博客 ” ，链接：http://blog.itpub.net/12639172/viewspace-611753/，如需转载，请注明出处，否则将追究法律责任。

转载于:http://blog.itpub.net/12639172/viewspace-611753/