本文介绍了如何使用动态规划解决矩阵链乘法问题，包括C和C++的程序实现。通过示例解释了矩阵乘法的基础知识，并详细展示了如何计算最少的乘法次数来优化矩阵链的乘法过程。动态规划表格用于存储中间结果，从而降低时间复杂度到O(n^3)。
c语言中矩阵乘法
Here you will learn about Matrix Chain Multiplication with example and also get a program that implements matrix chain multiplication in C and C++.
在这里，您将通过示例学习矩阵链乘法，并获得一个用C和C ++实现矩阵链乘法的程序。
Before going to main problem first remember some basis.
在解决主要问题之前，首先要记住一些基础。
We know that, to multiply two matrices it is condition that, number of columns in first matrix should be equal to number of rows in second matrix. Let say there are two matrices A and B with dimensions A (2 x 3) and B (3 x 2).
我们知道，要乘以两个矩阵，必须满足以下条件：第一个矩阵中的列数应等于第二个矩阵中的行数。 假设存在两个矩阵A和B，它们的尺寸分别为A(2 x 3)和B(3 x 2)。
Let’s see an example.
让我们来看一个例子。
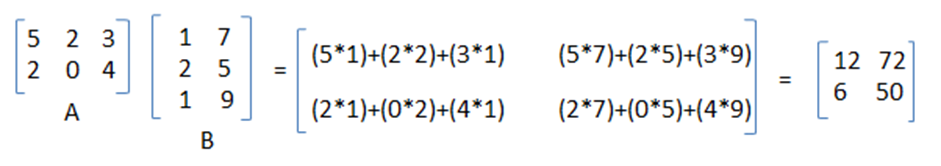
Above we can see resultant matrix is (2 x 2) matrix i.e. it contains total 4 elements. To calculate each element we did 3 multiplications (which is equal to number of columns in first matrix and number of rows in second matrix). So totally for 4 elements 4*3 = 12 multiplications are required.
在上面我们可以看到结果矩阵是(2 x 2)矩阵，即它总共包含4个元素。 为了计算每个元素，我们进行了3次相乘(等于第一个矩阵中的列数和第二个矩阵中的行数)。 因此，对于4个元素，总共需要4 * 3 = 12个乘法。
In generalized way matrices A (P x Q) and B(Q x R) will result matrix (P x R) which contains P * R elements. To calculate each element need “Q” number of multiplications. Total multiplications needed are P * Q * R
以通用方式，矩阵A(P x Q)和B(Q x R)将得出包含P * R元素的矩阵(P x R)。 要计算每个元素，需要“ Q”个乘法。 所需的总乘法为P * Q * R
Let’s try to multiply more than two matrices.
让我们尝试将两个以上的矩阵相乘。
If 3 matrices A, B ,C we can find the final result in two ways (AB)C or A(BC). We get same result in any way since matrix multiplication satisfies associativity property.
如果有3个矩阵A，B，C，我们可以通过两种方式(AB)C或A(BC)找到最终结果。 由于矩阵乘法满足关联性，因此无论如何我们都会得到相同的结果。
Let A (1 x 2 ), B (2 x 3 ), C ( 3 x 2 ). If we follow first way, i.e. (AB)C way.
设A(1 x 2)，B(2 x 3)，C(3 x 2)。 如果我们采用第一种方式，即(AB)C方式。
To calculate (AB) we need 1*2*3 = 6 multiplications. Now resultant AB get dimensions 1 x 3 this multiplied with C need 1*3*2 = 6 multiplications. Total 6+6 = 12 multiplications needed.
要计算(AB)，我们需要1 * 2 * 3 = 6乘法。 现在，所得的AB的尺寸为1 x 3乘以C，需要1 * 3 * 2 = 6乘法。 总共需要6 + 6 = 12个乘法。
If we follow second way, i.e. A(BC) way.
如果我们遵循第二种方法，即A(BC)方法。
To calculate (BC) we need 2*3*2 = 12 multiplications. Now resultant BC get dimensions 2 x 3. A multiplied with this result need 1*2*3 = 6. Total 12+6 = 18 multiplications needed.
要计算(BC)，我们需要2 * 3 * 2 = 12个乘法。 现在结果BC的尺寸为2 x3。乘以该结果需要1 * 2 * 3 =6。总共需要12 + 6 = 18个乘法。
Here we can observe that based on the way we parenthesize the matrices total number of multiplications are changing.
在这里，我们可以观察到，根据我们对矩阵加括号的方式，乘法的总数正在变化。
If 4 matrices A, B, C, D we can find final result in 5 ways A(B(CD)) or A((BC)(D)) or (AB)(CD) 4. ((AB)C)D or (A(BC))D. In this case also each way requires different number of multiplications.
如果有4个矩阵A，B，C，D，我们可以通过5种方式A(B(CD))或A((BC)(D))或(AB)(CD) 4找到最终结果。 ((AB)C) D或(A(BC))D。 在这种情况下，每种方式也需要不同数量的乘法。
General formula to find number of ways we can find solution is (2n)! / [ (n+1)! n! ]. After parenthesizing these many ways each way requires different number of multiplications for final result. When dimensions are large (200 x 250 like this) with more number of matrices, then finding the parenthesizing way which requires minimum number of multiplications need will gives less time complexity.
求公式的通用公式数量为(2n)！ / [(n + 1)！ n！ ]。 在用括号括起来的许多方法中，每种方法都需要不同数量的乘法才能得出最终结果。 当尺寸较大(如200 x 250这样)且矩阵数量较多时，找到需要最少乘法次数的括号化方法将减少时间复杂度。
So Matrix Chain Multiplication problem aim is not to find the final result of multiplication, it is finding how to parenthesize matrices so that, requires minimum number of multiplications.
因此矩阵链乘法问题的目的不是要找到乘法的最终结果，而是要找到括号的矩阵，因此需要最少的乘法运算。
Efficient way of solving this is using dynamic programming
解决此问题的有效方法是使用动态编程
使用动态规划的矩阵链乘法 (Matrix Chain Multiplication Using Dynamic Programming)
Let we have “n” number of matrices A1, A2, A3 ……… An and dimensions are d0 x d1, d1 x d2, d2 x d3 …………. dn-1 x dn (i.e Dimension of Matrix Ai is di-1 x di
让我们有n个矩阵A1，A2，A3…………an，维数为d0 x d1，d1 x d2，d2 x d3…………。 d n-1 xd n (即矩阵A i的维数是d i-1 xd i
Solving a chain of matrix that, Ai Ai+1 Ai+2 Ai+3 ……. Aj = (Ai Ai+1 Ai+2 Ai+3 ……. Ak ) (Ak+1 Ak+2 ……. Aj ) + di-1 dk dj where i <= k < j.
求解矩阵链，即A i A i + 1 A i + 2 A i + 3 ……。 A j =(A i A i + 1 A i + 2 A i + 3 ....... A k )(A k + 1 A k + 2 ....... A j )+ d i-1 d k d j其中i <= k <j。
For more understanding check below example.
要了解更多信息，请查看以下示例。
Here total i to j matrices, Matrix i to k and Matrix k+1 to j should be solved in recursive way and finally these two matrices multiplied and these dimensions di-1 dk dj (number of multiplications needed) added. The variable k is changed i to j.
在这里，应该以递归的方式求解总i至j矩阵，矩阵i至k和矩阵k + 1至j，最后将这两个矩阵相乘，然后将这些维d i-1 d k d j (所需的乘法数)相加。 变量k从i更改为j。
Recursive Equation
递归方程
Note: M[i, j] indicates that if we split from matrix i to matrix j then minimum number of scalar multiplications required.
注意： M [i，j]表示，如果我们从矩阵i拆分为矩阵j，则所需的标量乘法次数最少。
M [ i , j ] = { 0 ; when i=j ; [means it is a single matrix . If there is only one matrix no need to multiply with any other. So 0 (zero) multiplications required.]
M [i，j] = {0; 当i = j; [表示它是单个矩阵。 如果只有一个矩阵，则无需与其他任何矩阵相乘。 因此需要0(零)乘法。]
= { min { M[ i, k ] + M[k+1, j ] + di-1 dk dj } where i <= k< j
= {min {M [i，k] + M [k + 1，j] + d i-1 d k d j }其中i <= k <j
Example Problem
示例问题
Given problem: A1 (10 x 100), A2 (100 x 20), A3(20 x 5), A4 (5 x 80)
给定的问题：A1(10 x 100)，A2(100 x 20)，A3(20 x 5)，A4(5 x 80)
To store results, in dynamic programming we create a table
为了存储结果，在动态编程中我们创建一个表
| 1,1=0 | 2,2=0 | 3,3=0 | 4,4=0 |
| 1,2=20000 | 2,3=10000 | 3,4=8000 | |
| 1,3=15000 | 2,4=50000 | ||
| 1,4=19000 | |||
| 1,1 = 0 | 2,2 = 0 | 3,3 = 0 | 4,4 = 0 |
| 1,2 = 20000 | 2,3 = 10000 | 3,4 = 8000 | |
| 1,3 = 15000 | 2,4 = 50000 | ||
| 1,4 = 19000 | |||
This table filled using below calculations.
该表使用以下计算填充。
Here cell 2,3 stores the minimum number of scalar multiplications required to.
此处的单元格2,3存储所需的最小标量乘法次数。
Using above recursive equation we can fill entire first row with all 0’s (zeros) because i=j (i.e. split happened at only one matrix which requires zero multiplications)
使用上面的递归方程，我们可以用全0(零)填充整个第一行，因为i = j(即，拆分仅发生在需要零乘法的一个矩阵上)
Table [1,2] = 10*100*20 = 20000
表[1,2] = 10 * 100 * 20 = 20000
Table [2,3] = 100*20*5 = 10000
表[2,3] = 100 * 20 * 5 = 10000
Table [3,4] = 20*5*80 = 8000
表[3,4] = 20 * 5 * 80 = 8000
Table [1,3] = minimum of
表[1,3] =最小值
= { (1,1) + (2,3) + 10* 100*5 = 0+10000+5000 = 15000
= {(1,1)+(2,3)+ 10 * 100 * 5 = 0 + 10000 + 5000 = 15000
= { (1,2) + (3,3) + 10*20*5 = 20000+0+1000 = 21000
= {(1,2)+(3,3)+ 10 * 20 * 5 = 20000 + 0 + 1000 = 21000
Therefore Table[1,3] is 15000 and split happened at 1
因此，Table [1,3]为15000，拆分发生在1
Table [2,4] = minimum of
表[2,4] =最小值
= { (2,2) +(3,4) + 100*20*80 = 0 + 8000 + 160000 = 168000
= {(2,2)+(3,4)+ 100 * 20 * 80 = 0 + 8000 + 160000 = 168000
= { (2,3) + (4,4) + 100*5*80 = 10000 + 0 + 40000 = 50000
= {(2,3)+(4,4)+ 100 * 5 * 80 = 10000 + 0 + 40000 = 50000
Therefore Table of [2,4] is 50000 and split happened at 3
因此，[2,4]的表为50000，分裂发生在3
Table of [1,4] = minimum of
表格[1,4] =最小值
= { (1,1) +(2,4) + 10*100*80 = 0 + 50000 + 80000 = 130000
= {(1,1)+(2,4)+ 10 * 100 * 80 = 0 + 50000 + 80000 = 130000
= { (1,2) +(3,4) + 10* 20* 80 = 20000 + 8000 + 16000 = 44000
= {(1,2)+(3,4)+ 10 * 20 * 80 = 20000 + 8000 + 16000 = 44000
= { (1,3) + (4,4) + 10*5*80 = 15000+0+4000 = 19000
= {(1,3)+(4,4)+ 10 * 5 * 80 = 15000 + 0 + 4000 = 19000
Therefore table of [1,4] is 19000 which is final answer and split happened at 3.
因此，[1,4]的表是19000，这是最终答案，分裂发生在3。
Splitting way: (1234) is original in final outcome where 19000 answer we got split happened at 3 so ( 1 2 3 ) (4). Split for (123) means see at Table [1,3] that one minimum 15000 split at 1 . So ( ( 1 ) ( 2 3 ) ) ( 4). That means first do 2 x 3 and this 1 x first result and then this result x 4.
拆分方式：(1234)是最终结果中的原始结果，其中我们拆分的19000个答案发生在3 so(1 2 3)(4)。 为(123)拆分表示在表[1,3]处至少有15000个拆分为1。 因此((1)(2 3))(4) 。 这意味着先做2 x 3，然后再做1x，然后再做结果x 4。
Time Complexity
时间复杂度
If there are n number of matrices we are creating a table contains [(n) (n+1) ] / 2 cells that is in worst case total number of cells n*n = n2 cells we need calculate = O (n2)
如果存在n个矩阵，我们将创建一个包含[(n)(n + 1)] / 2个单元的表，在最坏的情况下，该单元的总数n * n = n 2个单元，我们需要计算= O(n 2 )
For each one of entry we need find minimum number of multiplications taking worst (it happens at last cell in table) that is Table [1,4] which equals to O (n) time.
对于每一项，我们都需要找到最差的最小乘法次数(发生在表的最后一个单元格)，即表[1,4]，等于O(n)时间。
Finally O (n2) * O (n) = O (n3) is time complexity.
最后， O(n 2 )* O(n)= O(n 3 )是时间复杂度。
Space Complexity
空间复杂度
We are creating a table of n x n so space complexity is O (n2).
我们正在创建一个nxn表，因此空间复杂度为O(n 2 )。
C中的矩阵链乘法程序 (Program for Matrix Chain Multiplication in C)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
// This code implemented using Algorithm in Coremen book
#include<stdio.h>
#include<limits.h>
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
int MatrixChainMultiplication(int p[], int n)
{
int m[n][n];
int i, j, k, L, q;
for (i=1; i<n; i++)
m[i][i] = 0; //number of multiplications are 0(zero) when there is only one matrix
//Here L is chain length. It varies from length 2 to length n.
for (L=2; L<n; L++)
{
for (i=1; i<n-L+1; i++)
{
j = i+L-1;
m[i][j] = INT_MAX; //assigning to maximum value
for (k=i; k<=j-1; k++)
{
q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (q < m[i][j])
{
m[i][j] = q; //if number of multiplications found less that number will be updated.
}
}
}
}
return m[1][n-1]; //returning the final answer which is M[1][n]
}
int main()
{
int n,i;
printf("Enter number of matrices\n");
scanf("%d",&n);
n++;
int arr[n];
printf("Enter dimensions \n");
for(i=0;i<n;i++)
{
printf("Enter d%d :: ",i);
scanf("%d",&arr[i]);
}
int size = sizeof(arr)/sizeof(arr[0]);
printf("Minimum number of multiplications is %d ", MatrixChainMultiplication(arr, size));
return 0;
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
// This code implemented using Algorithm in Coremen book
#include<stdio.h>
#include<limits.h>
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
int MatrixChainMultiplication ( int p [ ] , int n )
{
int m [ n ] [ n ] ;
int i , j , k , L , q ;
for ( i = 1 ; i < n ; i ++ )
m [ i ] [ i ] = 0 ; //number of multiplications are 0(zero) when there is only one matrix
//Here L is chain length. It varies from length 2 to length n.
for ( L = 2 ; L < n ; L ++ )
{
for ( i = 1 ; i < n - L + 1 ; i ++ )
{
j = i + L - 1 ;
m [ i ] [ j ] = INT_MAX ; //assigning to maximum value
for ( k = i ; k <= j - 1 ; k ++ )
{
q = m [ i ] [ k ] + m [ k + 1 ] [ j ] + p [ i - 1 ] * p [ k ] * p [ j ] ;
if ( q < m [ i ] [ j ] )
{
m [ i ] [ j ] = q ; //if number of multiplications found less that number will be updated.
}
}
}
}
return m [ 1 ] [ n - 1 ] ; //returning the final answer which is M[1][n]
}
int main ( )
{
int n , i ;
printf ( "Enter number of matrices\n" ) ;
scanf ( "%d" , & n ) ;
n ++ ;
int arr [ n ] ;
printf ( "Enter dimensions \n" ) ;
for ( i = 0 ; i < n ; i ++ )
{
printf ( "Enter d%d :: " , i ) ;
scanf ( "%d" , & arr [ i ] ) ;
}
int size = sizeof ( arr ) / sizeof ( arr [ 0 ] ) ;
printf ( "Minimum number of multiplications is %d " , MatrixChainMultiplication ( arr , size ) ) ;
return 0 ;
}
|
Output
输出量
Enter number of matrices 4 Enter dimensions Enter d0 :: 10 Enter d1 :: 100 Enter d2 :: 20 Enter d3 :: 5 Enter d4 :: 80 Minimum number of multiplications is 19000
输入矩阵数 4 输入维数 输入d0 :: 10 输入d1 :: 100 输入d2 :: 20 输入d3 :: 5 输入d4 :: 80 最小乘法数为19000
C ++中的矩阵链乘法程序 (Program for Matrix Chain Multiplication in C++)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
// This code implemented using Algorithm in Coremen book
#include<iostream>
#include<limits.h>
using namespace std;
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
int MatrixChainMultiplication(int p[], int n)
{
int m[n][n];
int i, j, k, L, q;
for (i=1; i<n; i++)
m[i][i] = 0; //number of multiplications are 0(zero) when there is only one matrix
//Here L is chain length. It varies from length 2 to length n.
for (L=2; L<n; L++)
{
for (i=1; i<n-L+1; i++)
{
j = i+L-1;
m[i][j] = INT_MAX; //assigning to maximum value
for (k=i; k<=j-1; k++)
{
q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (q < m[i][j])
{
m[i][j] = q; //if number of multiplications found less that number will be updated.
}
}
}
}
return m[1][n-1]; //returning the final answer which is M[1][n]
}
int main()
{
int n,i;
cout<<"Enter number of matrices\n";
cin>>n;
n++;
int arr[n];
cout<<"Enter dimensions \n";
for(i=0;i<n;i++)
{
cout<<"Enter d"<<i<<" :: ";
cin>>arr[i];
}
int size = sizeof(arr)/sizeof(arr[0]);
cout<<"Minimum number of multiplications is "<<MatrixChainMultiplication(arr, size));
return 0;
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
// This code implemented using Algorithm in Coremen book
#include<iostream>
#include<limits.h>
using namespace std ;
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
int MatrixChainMultiplication ( int p [ ] , int n )
{
int m [ n ] [ n ] ;
int i , j , k , L , q ;
for ( i = 1 ; i < n ; i ++ )
m [ i ] [ i ] = 0 ; //number of multiplications are 0(zero) when there is only one matrix
//Here L is chain length. It varies from length 2 to length n.
for ( L = 2 ; L < n ; L ++ )
{
for ( i = 1 ; i < n - L + 1 ; i ++ )
{
j = i + L - 1 ;
m [ i ] [ j ] = INT_MAX ; //assigning to maximum value
for ( k = i ; k <= j - 1 ; k ++ )
{
q = m [ i ] [ k ] + m [ k + 1 ] [ j ] + p [ i - 1 ] * p [ k ] * p [ j ] ;
if ( q < m [ i ] [ j ] )
{
m [ i ] [ j ] = q ; //if number of multiplications found less that number will be updated.
}
}
}
}
return m [ 1 ] [ n - 1 ] ; //returning the final answer which is M[1][n]
}
int main ( )
{
int n , i ;
cout << "Enter number of matrices\n" ;
cin >> n ;
n ++ ;
int arr [ n ] ;
cout << "Enter dimensions \n" ;
for ( i = 0 ; i < n ; i ++ )
{
cout << "Enter d" << i << " :: " ;
cin >> arr [ i ] ;
}
int size = sizeof ( arr ) / sizeof ( arr [ 0 ] ) ;
cout << "Minimum number of multiplications is " << MatrixChainMultiplication ( arr , size ) ) ;
return 0 ;
}
|
Comment below if you have any queries related to above program for matrix chain multiplication in C and C++.
如果您有任何与上述程序有关C和C ++中的矩阵链乘法的查询，请在下面评论。
翻译自: https://www.thecrazyprogrammer.com/2017/05/matrix-chain-multiplication.html
c语言中矩阵乘法
扫一扫
2176
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
