推荐算法示例_最佳合并模式（算法和示例）

推荐算法示例

Optimal merge pattern is a pattern that relates to the merging of two or more sorted files in a single sorted file. This type of merging can be done by the two-way merging method.

最佳合并模式是与将两个或多个已排序文件合并到单个已排序文件中有关的模式。 可以通过双向合并方法完成这种合并。

If we have two sorted files containing n and m records respectively then they could be merged together, to obtain one sorted file in time O (n+m).

如果我们有两个分别包含n和m个记录的排序文件，则可以将它们合并在一起，以获得时间为O(n + m)的一个排序文件。

There are many ways in which pairwise merge can be done to get a single sorted file. Different pairings require a different amount of computing time.The main thing is to pairwise merge the n sorted files so that the number of comparisons will be less.

成对合并有很多方法可以获取单个排序文件。 不同的配对需要不同的计算时间。主要是成对合并n个排序的文件，这样比较的次数将减少。

The formula of external merging cost is:

外部合并成本的公式为：

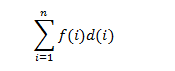
Where, f (i) represents the number of records in each file and d (i) represents the depth.

其中， f(i)表示每个文件中的记录数， d(i)表示深度。

最佳合并模式的算法 (Algorithm for optimal merge pattern )

Algorithm Tree(n)
//list is a global list of n single node 
{
	For  i=1 to i= n-1 do
	{
		// get a new tree node
		Pt: new treenode; 
		// merge two trees with smallest length
		(Pt = lchild) = least(list); 
		(Pt = rchild) = least(list); 
		(Pt =weight) = ((Pt = lchild) = weight) = ((Pt = rchild) = weight);
		Insert (list , Pt);
	}
	// tree left in list 
	Return least(list); 
}

An optimal merge pattern corresponds to a binary merge tree with minimum weighted external path length. The function tree algorithm uses the greedy rule to get a two- way merge tree for n files. The algorithm contains an input list of n trees. There are three field child, rchild, and weight in each node of the tree. Initially, each tree in a list contains just one node. This external node has lchild and rchild field zero whereas weight is the length of one of the n files to be merged. For any tree in the list with root node t, t = it represents the weight that gives the length of the merged file. There are two functions least (list) and insert (list, t) in a function tree. Least (list) obtains a tree in lists whose root has the least weight and return a pointer to this tree. This tree is deleted from the list. Function insert (list, t) inserts the tree with root t into the list.

最佳合并模式对应于具有最小加权外部路径长度的二进制合并树。 函数树算法使用贪婪规则为n个文件获取双向合并树。 该算法包含n个树的输入列表。 树的每个节点中都有三个字段child， rchild和weight。 最初，列表中的每棵树仅包含一个节点。 该外部节点的lchild和rchild字段为零，而weight是要合并的n个文件之一的长度。 对于列表中根节点为t的任何树， t =它表示给出合并文件长度的权重。 函数树中最少有两个函数( list )和插入(list，t) 。 最小( list )在列表中获得一棵树，其根的权重最小，并返回指向该树的指针。 该树将从列表中删除。 函数insert(list，t)将根为t的树插入到列表中。

The main for loop in this algorithm is executed in n-1 times. If the list is kept in increasing order according to the weight value in the roots, then least (list) needs only O(1) time and insert (list, t) can be performed in O(n) time. Hence, the total time taken is O (n2). If the list is represented as a minheap in which the root value is less than or equal to the values of its children, then least (list) and insert (list, t) can be done in O (log n) time. In this condition, the computing time for the tree is O (n log n).

该算法中的main for循环执行n-1次。 如果列表根据根中的权重值按升序排列，则最小(列表)仅需要O(1)时间，而插入(列表，t)则可以在O(n)时间执行 。 因此，花费的总时间为O(n2) 。 如果列表表示为根值小于或等于其子代值的minheap，则可以在O(log n)时间内完成最小(list)和插入(list，t) 。 在这种情况下，树的计算时间为O(n log n) 。

Example:

例：

Given a set of unsorted files: 5, 3, 2, 7, 9, 13

给定一组未排序的文件：5、3、2、7、9、13

Now, arrange these elements in ascending order: 2, 3, 5, 7, 9, 13

现在，按升序排列这些元素：2、3、5、7、9、13

After this, pick two smallest numbers and repeat this until we left with only one number.

此后，选择两个最小的数字并重复此操作，直到我们只剩下一个数字。

Now follow following steps:

现在，请按照以下步骤操作：

Step 1: Insert 2, 3

步骤1：插入2、3

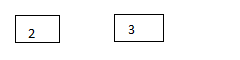
Step 2:

第2步：

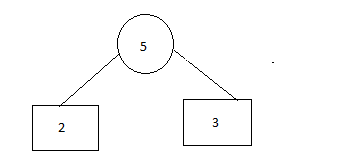
Step 3: Insert 5

步骤3：插入5

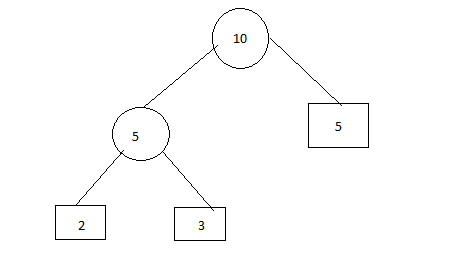
Step 4: Insert 13

步骤4：插入13

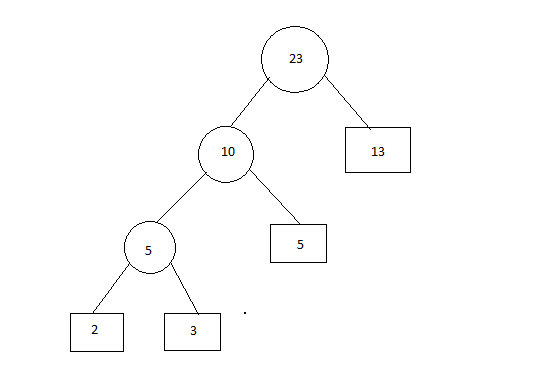
Step 5: Insert 7 and 9

步骤5：插入7和9

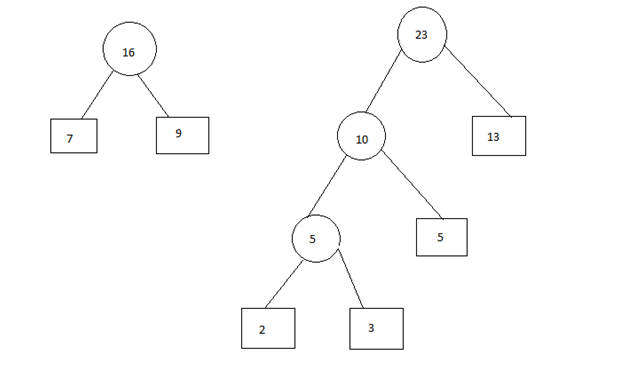
Step 6:

步骤6：

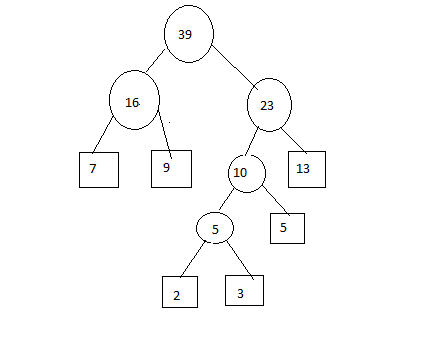
So, The merging cost = 5 + 10 + 16 + 23 + 39 = 93

因此，合并成本= 5 + 10 + 16 + 23 + 39 = 93

翻译自: https://www.includehelp.com/algorithms/optimal-merge-pattern-algorithm-and-example.aspx

推荐算法示例