最长递增子序列 子串_最长递增子序列

最长递增子序列 子串

Description:

描述：

This is one of the most popular dynamic programming problems often used as building block to solve other problems.

这是最流行的动态编程问题之一，通常用作解决其他问题的基础。

Problem statement:

问题陈述：

Given a sequence A of size N, find the length of the longest increasing subsequence from the given sequence.

给定一个大小为N的序列A ，从给定序列中找到最长的递增子序列的长度 。

The longest increasing subsequence means to find a subsequence of a given sequence where the subsequence's elements are sorted in increasing order, and the subsequence is longest possible. This subsequence is not necessarily contiguous, or unique. Longest increasing subsequence is strictly increasing.

最长的增长子序列意味着找到给定序列的子序列，其中该子序列的元素按升序排序，并且该子序列可能最长。 该子序列不一定是连续的或唯一的。 最长增加的子序列严格增加。

    Input:
    N=7
    Sequence:
    {2, 3, 4, 0, 1, 2, 3, 8, 6, 4}

    Output:
    Length of Longest increasing subsequence is 5
    Longest increasing subsequence= {0, 1, 2, 3, 8} or {0, 1, 2, 3, 4}

Explanation with example

举例说明

The possible increasing sub-sequences are,

可能增加的子序列是

Of Length 1 //each element itself is an increasing sequence

长度为1 //每个元素本身都是递增序列

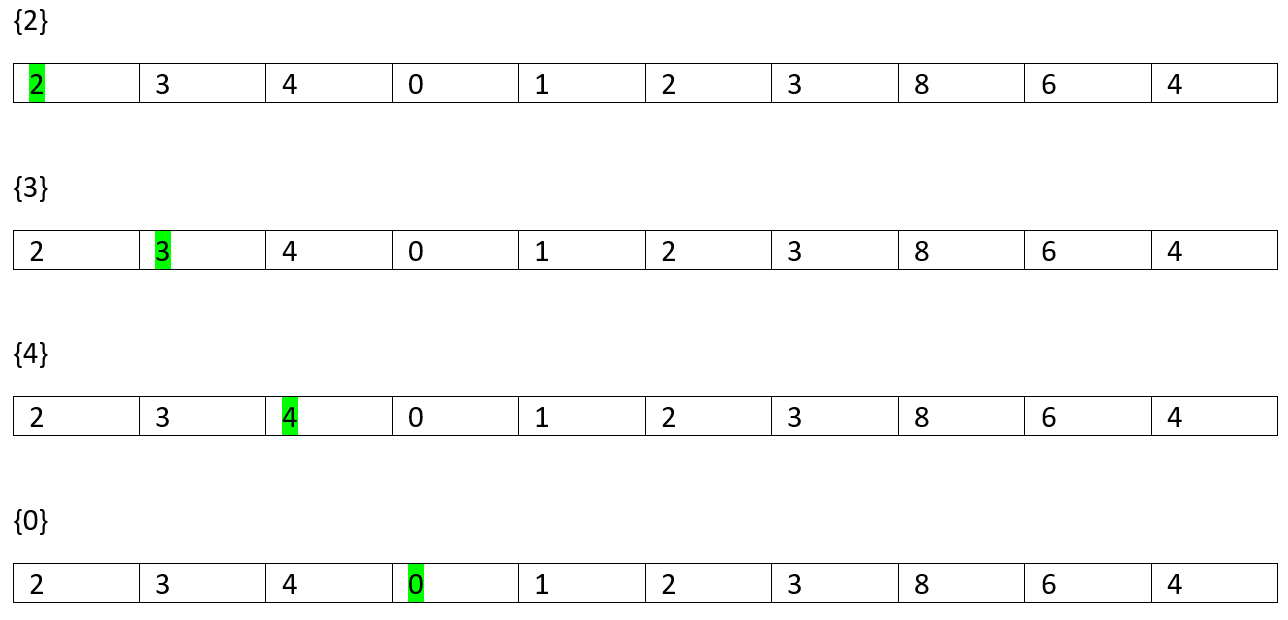
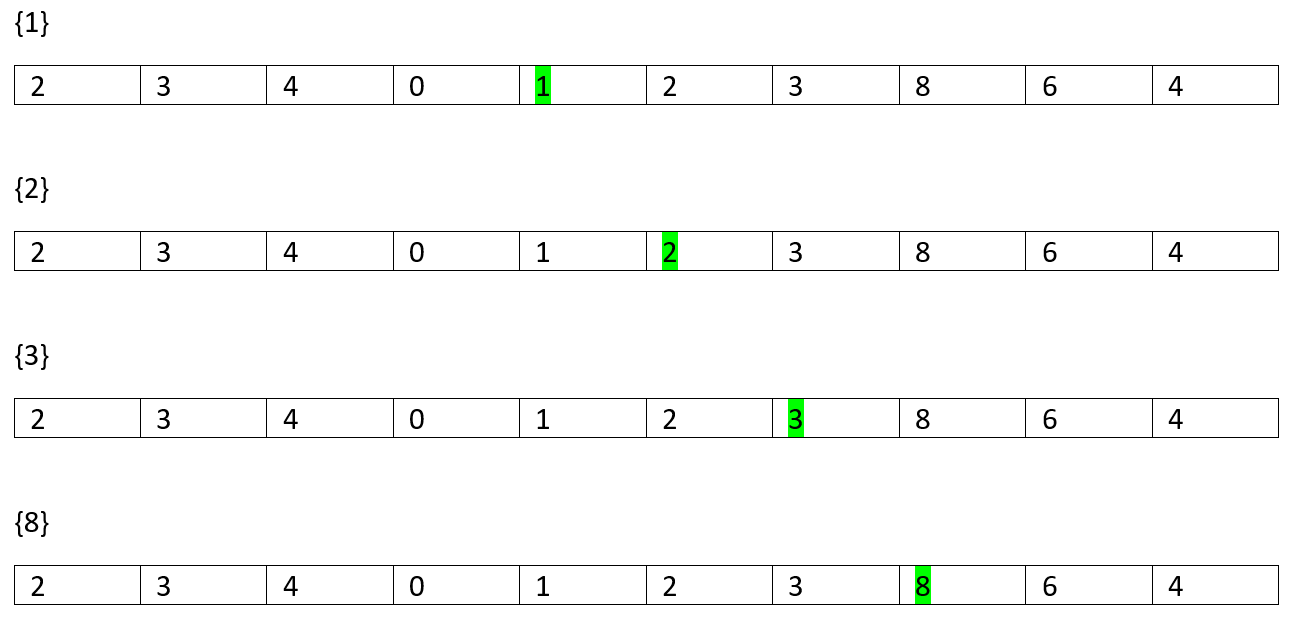
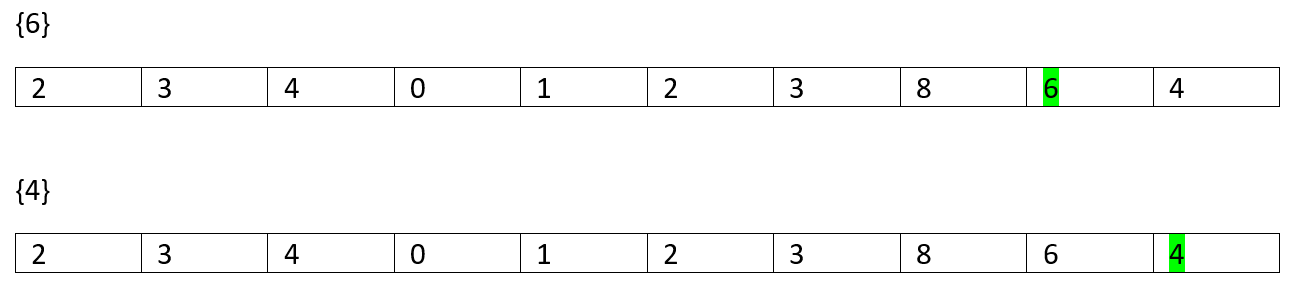
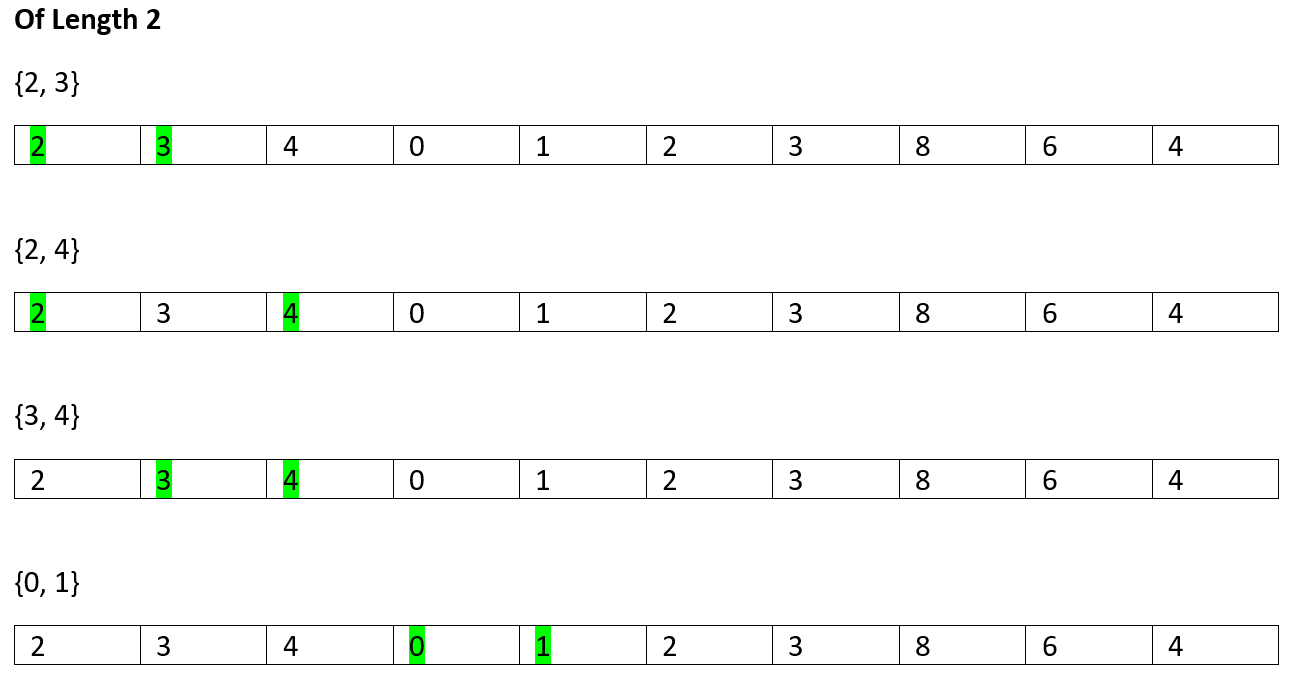
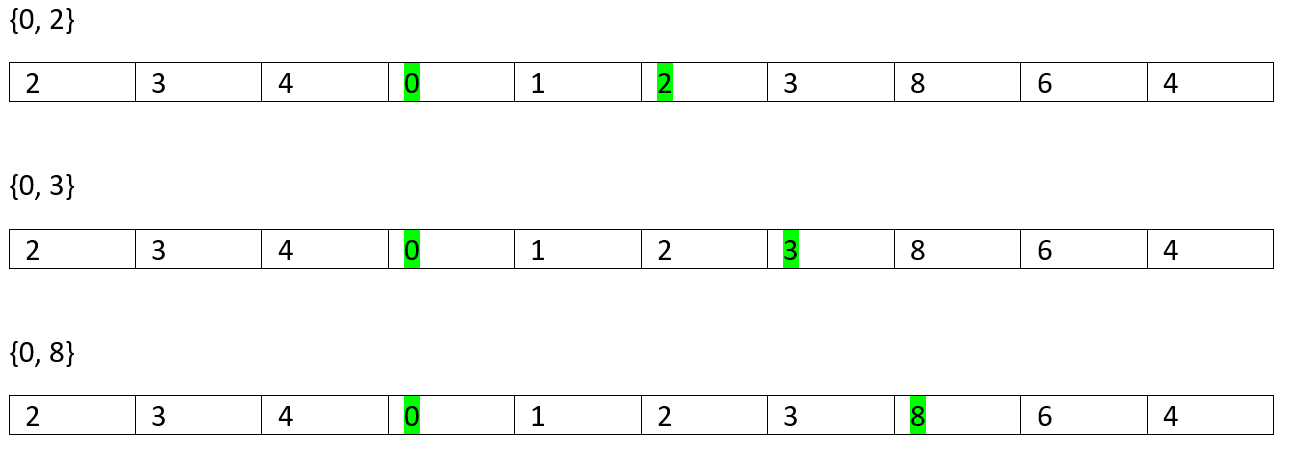
So, on...

所以...

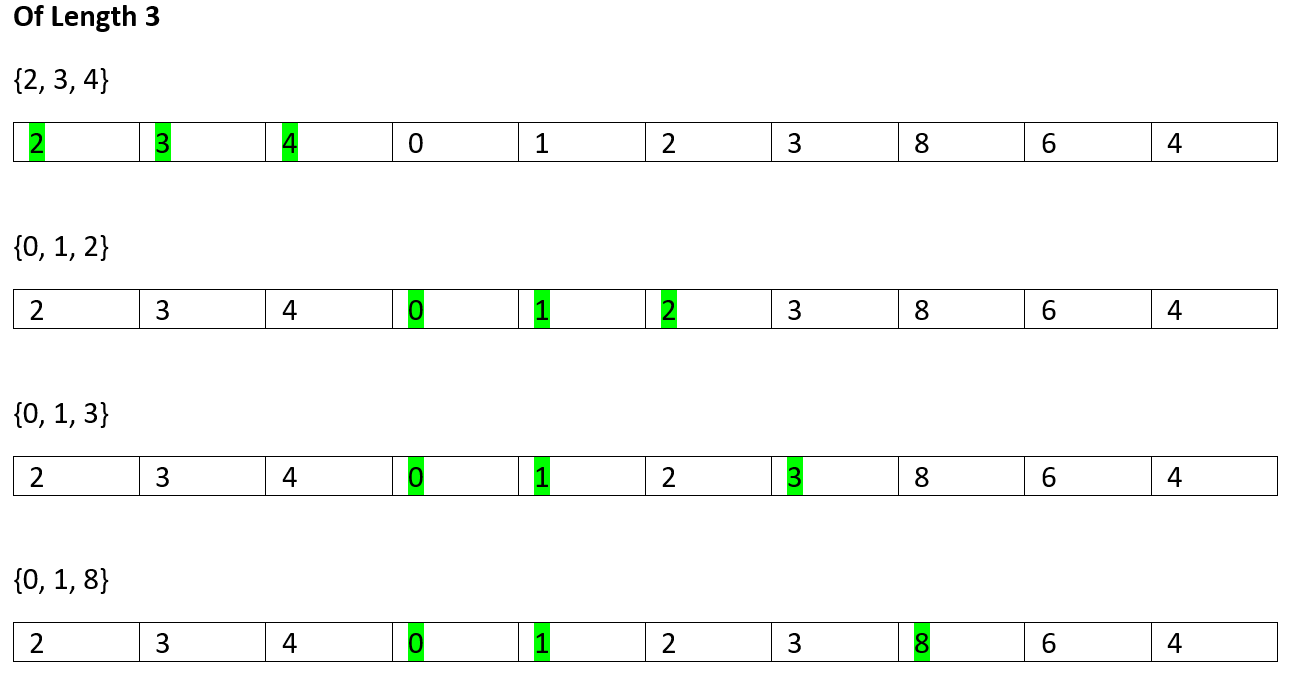
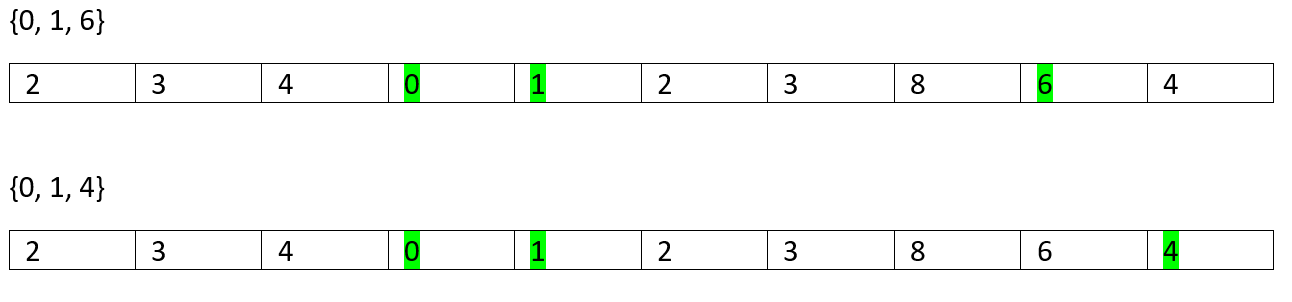
So, on...

所以...

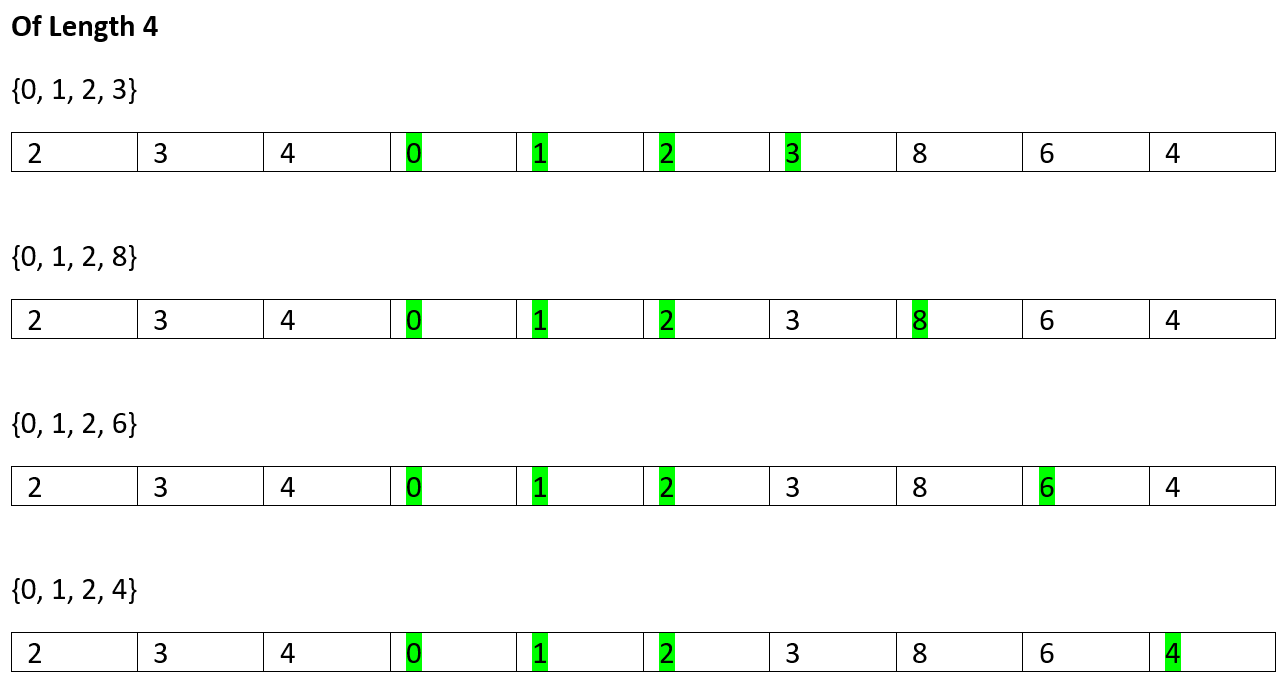
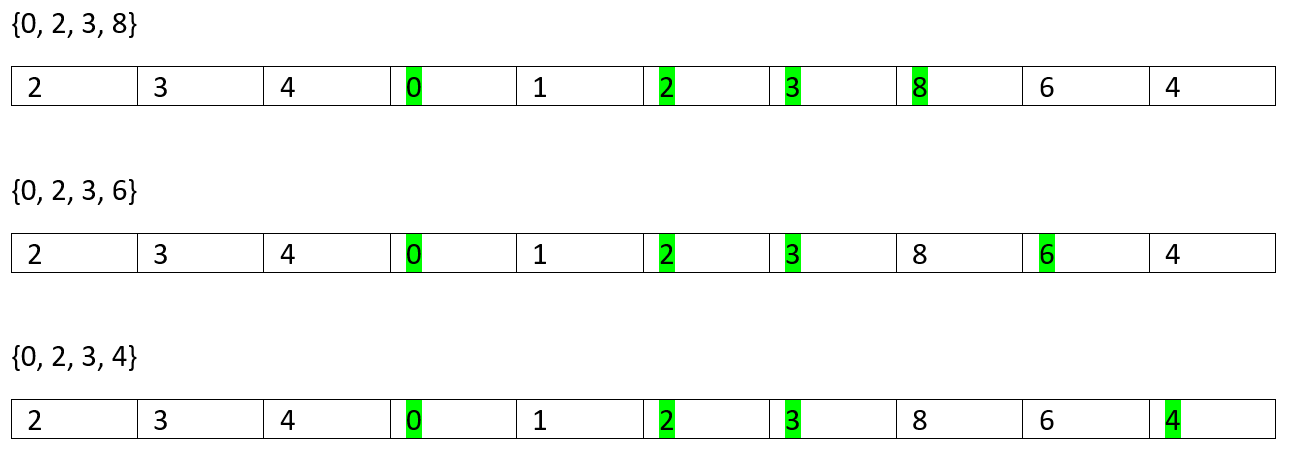
So, on...

所以...

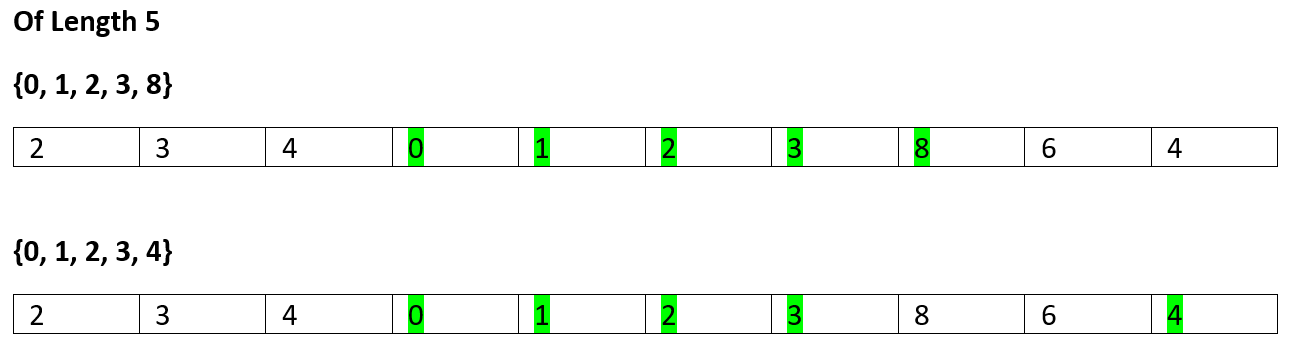
No more
Of Length 6
None

不再
长度6
没有

So, the longest increasing subsequence length is 5.

因此，最长的递增子序列长度是5。

问题解决方法 (Problem Solution Approach)

Of course, in brute-force we can simply generate all increasing sequences and find the longest one. But it would take exponential time which is not a feasible solution. Hence, we choose Dynamic programming to solve.

当然，在蛮力作用下，我们可以简单地生成所有递增的序列并找到最长的序列。 但是，这将花费指数时间，这不是可行的解决方案。 因此，我们选择动态规划来解决。

We create a DP table to store longest increasing subsequence length.
It's intuitive that the minimum value would be 1 as each element represents the primitive sequence which is an increasing one.

我们创建一个DP表来存储最长的递增子序列长度。
直观的是，最小值将为1，因为每个元素代表原始序列，该序列是递增的。

So, the base value is 1.

因此，基准值为1。

Now,

现在，

    Lis(i) = longest increasing subsequence starting from index 0 to index i

So,
To compute L(i) the recursion function is,

所以，
为了计算L(i) ，递归函数为

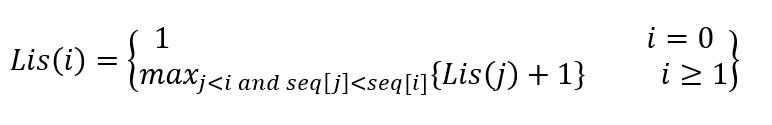
As, the base value is 1, for every index i, L(i) is at least 1.

这样，对于每个索引i ，基值为1， L(i)至少为1。

    
    1) Create the DP array, Lis[n]
    2) Initialize the DP array.
        for i=0 to n-1
            lis[i]=1;
    3) Now, to compute the Lis[i]
    for index  i=1 to n-1         
        for previous index j=0 to i-1
            // if (arr[i],arr[j]) is inceasing sequence
            if(lis[i]<lis[j]+1 && a[i]>a[j])
                lis[i]=lis[j]+1;
        end for
    end for 

Initially DP table,

最初是DP表，

So, the maximum out of this is 5
Hence, LIS=5.

因此，最大数量为5
因此，LIS ＝ 5。

C++ implementation:

C ++实现：

#include <bits/stdc++.h>
using namespace std;

int max(int a, int b)
{
    if (a > b)
        return a;
    else
        return b;
}

int LIS(vector<int> a, int n)
{
    int lis[n];

    //base case
    for (int i = 0; i < n; i++)
        lis[i] = 1;

    //fill up table
    for (int i = 1; i < n; i++) {

        for (int j = 0; j < i; j++) {
            if (lis[i] < lis[j] + 1 && a[i] > a[j])
                lis[i] = lis[j] + 1;
        }
    }
    //return LIS
    return *max_element(lis, lis + n);
}
int main()
{
    int n, item;

    cout << "Sequence size:\n";
    scanf("%d", &n);
    //input the array
    vector<int> a;
    cout << "Input sequence:\n";
    for (int j = 0; j < n; j++) {
        scanf("%d", &item);
        a.push_back(item);
    }

    cout << "Length of longest incresing subsequence is: " << LIS(a, n) << endl;

    return 0;
}

Output

输出量

Sequence size:
10
Input sequence:
2 3 4 0 1 2 3 8 6 4
Length of longest incresing subsequence is: 5

翻译自: https://www.includehelp.com/icp/longest-increasing-subsequence.aspx

最长递增子序列 子串